Question
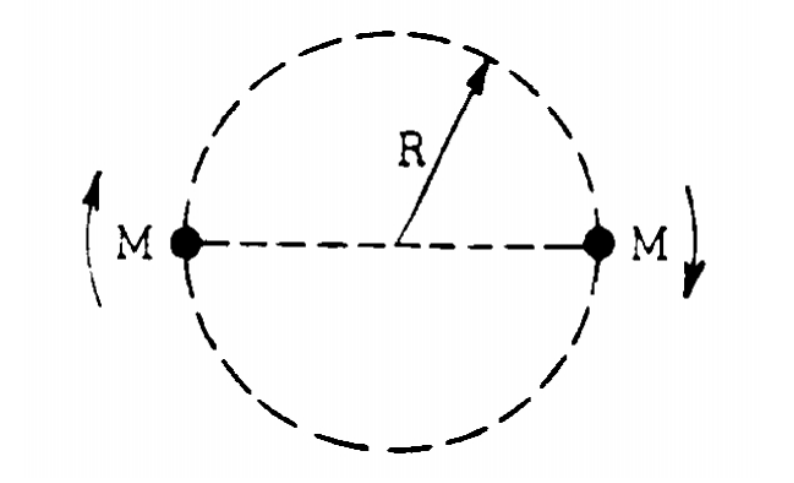
Two stars each of mass M form a binary star system such that both stars move in the same circular orbit of radius R. The universal gravitational constant is G.
a. Use Newton’s laws of motion and gravitation to find an expression for the speed v of either star in terms of R, G, and M.
b. Express the total energy E of the binary star system in terms of R, G, and M.
Suppose instead, one of the stars had a mass 2M.
c. On the following diagram, show circular orbits for this star system.
![]()
d. Find the ratio of the speeds, v2M/vM.
▶️Answer/Explanation
Ans:
a. Fg = Fc gives \(\frac{GMM}{(2R)^{2}}=\frac{Mv^{2}}{R}.\) Solving for v gives v = \(\frac{1}{2} |\frac{\overline{GM}}{R}\)
b. E = PE + KE = – \(\frac{GMM}{2R}+ 2\left ( \frac{1}{2} Mv^{2}\right )= -\frac{GMM}{2R}+2\left ( \frac{1}{2}M\left ( \frac{1}{2}|\frac{\overline{GM}}{R} \right )^{2} \right ) = – \frac{GM^{2}}{4R}\)
c. 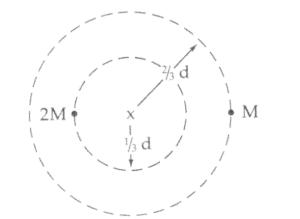
d. Fg2 = Fg1 = Fc
\(\frac{(2M){v_{1}}^{2}}{1/3^{d}}= \frac{M{v_{2}}^{2}}{2/3^{d}}\) gives v2/v1 = ½
Question
(a) A fellow student argues that you cannot use the formula \(1/2gt^{2}\) to find the height of a very tall cliff (200 meters or so) when dropping a stone from the top and counting the seconds until impact at the bottom. He says that because of Newton’s law of universal gravity, the acceleration is not constant during the fall. Using equations and calculations, both support and refute his argument. Would his argument have had greater, lesser, or the same power to persuade you if he was talking about a cliff on the Moon? Why or why not?
(b) Two masses, M and 9M , are separated by a distance of d . At what distance and in what direction from the smaller mass should a third mass be placed such that the net gravitational force on this third mass is zero? There are two solutions. Find both.
▶️Answer/Explanation
Ans:
(a) First, technically your fellow student is correct. As the top of the cliff is 200 meters farther from the center of Earth, the gravitational field experienced by the rock at the top of the cliff is technically weaker:
\(g_{top}=GM_{Earth}/(R+200)^{2}\) versus \(g_{bottom}=GM_{Earth}/(R)^{2}\)
Since the radius of Earth is \(6.38\times10^{6}m\) , adding a mere 200 m does not make much of a difference: \(200/(6.38\times10^{6})=3\times10^{-5}\)
Therefore for all practical purposes, the difference in gravitational field strength is so minimal that treating g as a constant acceleration is fairly reasonable. On the moon, one would expect a greater deviance since 200 meters is a greater fraction of the Moon’s radius \((1.7\times10^{6})\). However, any decrease in the moon’s gravitational effects would also be negligible;
\(200/(1.7\times10^{6})=1\times10^{-4}\)
(b) Somewhere along a line between M and 9M but closer to M should be a position such that the force of attraction for M will cancel the force of attraction for 9M . Let the distance between the third mass ( m ) and M be x: \(GmM/x^{2}=Gm(9M)/(d-x)^{2}\)
Cancel and simplify: \(9x^{2}=(d-x)^{2}\)
Take the square root of both sides: \(\pm3x=d-x\)
This leads us to two solutions: \(x=d/4\)
which is the expected solution between the masses and
\(x=d/2\)
which is an unexpected solution on the outside of mass M along the same line. Note that in both solutions, the new mass m is 3 times farther away from 9M than it is from M .
