Question
An elevator ride consists of the following portions.
a. Initially, the elevator is on the ground floor and quickly speeds up in the upward direction on its way to the top floor.
b. Most of the trip upward is at a constant velocity. c. Suddenly, near the top floor, the elevator comes to a stop just in time for the top floor.
d. Now the button for the first floor is pressed, and the elevator speeds downward suddenly.
e. Most of the trip downward is spent at constant velocity.
f. Suddenly, at the very bottom, the elevator comes to a stop.
(a) Draw a qualitative free-body diagram (showing the relative vector sizes) for each portion of the elevator ride as experienced by a passenger. Next to each, describe how the person would feel (normal, heavier than usual, lighter than usual, etc.).
(b) Explain the difference among the passenger’s mass, gravitational weight, and apparent weight throughout the trip. When (if ever) are these the same, and when (if ever) are they different? Which quantities change during the trip, and which ones do not?
(c) Describe what would happen if, on the way up (during step (b)), the cables were to break. Ignore any frictional effect between the elevator itself and the elevator shaft. Be sure to include a discussion of the relative motion of the elevator car and the passenger. Your answer should include a discussion or sketch of the height above ground, the velocity, and the acceleration experienced by the passenger from the time of the break until the end of the motion.
(d) Sketch the expected behavior of the person’s height as a function of time for situation (c) above. Also sketch the person’s \(V_{y}\) as a function of time as well.
▶️Answer/Explanation
Ans:
(a) 





(b) A person’s mass is a measure of his or her inertia. This value does not change due to acceleration or changes in location. Gravitational weight is a force due to the interaction of the person’s mass and the planet on which he or she is standing (including the distance between their centers). Although technically this value is slightly smaller as you get higher above sea level, the differences within a building on Earth are negligible. Apparent weight is the contact forces your body experiences, which give you your subjective experience of “weight.” In this case, the normal force and the changing values of the normal force explain the changes the person would experience on the elevator ride.
(c) The elevator and passenger would experience free fall. The only force would be the downward mg , and the normal force would be zero. Hence, the person would feel weightless. Since the car was on the way up when the cables broke, both passenger and elevator would maintain the same relative velocity to each other as both continued upward, slowed down, and then reversed direction and continued to speed up while falling. The entire time, the passenger would feel weightless.
(d) 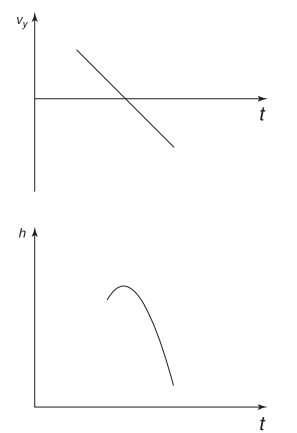
Question
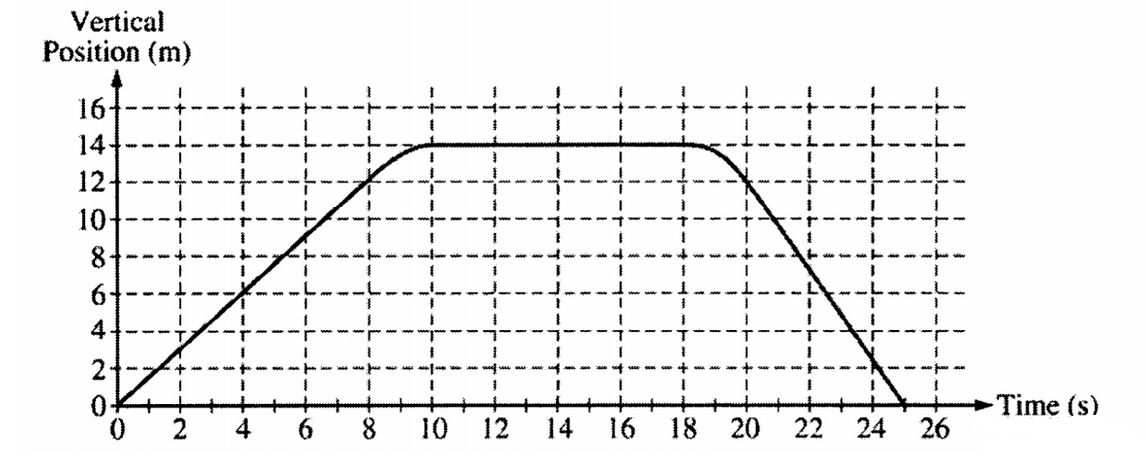
The vertical position of an elevator as a function of time is shown above.
a. On the grid below, graph the velocity of the elevator as a function of time.
b. i. Calculate the average acceleration for the time period t = 8 s to t = 10 s.
ii. On the box below that represents the elevator, draw a vector to represent the direction of this average acceleration.
▶️Answer/Explanation
Ans:
a. 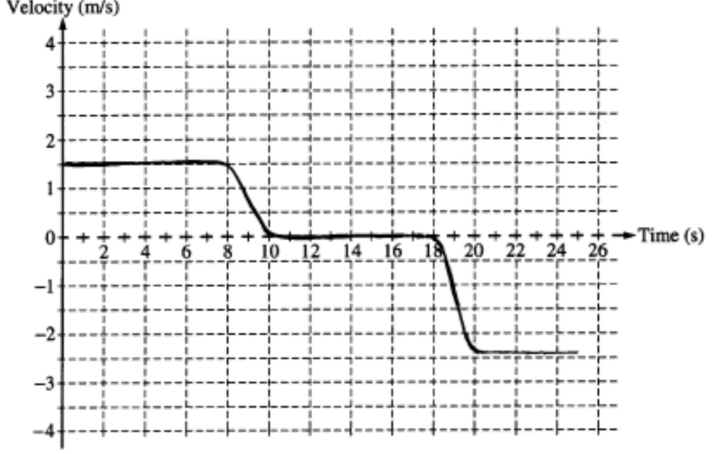
b. i. aavg = Δv/Δt = (0 – 1.5 m/s)/( 2 s) = – 0.75 m/s2
ii. 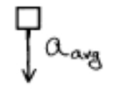
Question: (7 points, suggested time 13 minutes)
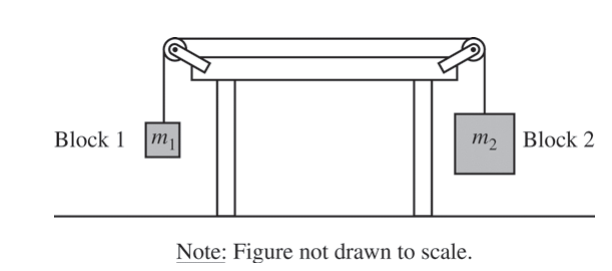
Two blocks are connected by a string of negligible mass that passes over massless pulleys that turn with negligible friction, as shown in the figure above. The mass m2 of block 2 is greater than the mass m1 of block 1. The blocks are released from rest.
(a) The dots below represent the two blocks. Draw free-body diagrams showing and labeling the forces (not components) exerted on each block. Draw the relative lengths of all vectors to reflect the relative magnitudes of all the forces.
(b) Derive the magnitude of the acceleration of block 2. Express your answer in terms of m1 , m2 , and g.
Block 3 of mass m3 is added to the system, as shown below. There is no friction between block 3 and the table.
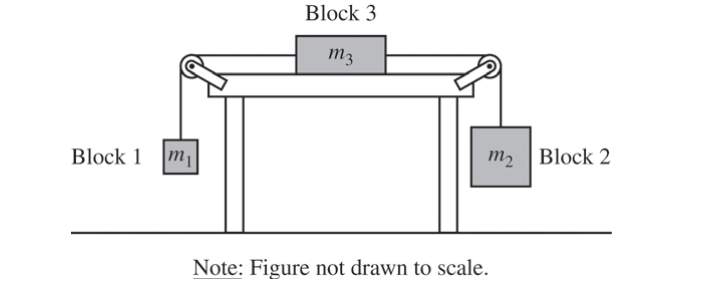
(c) Indicate whether the magnitude of the acceleration of block 2 is now larger, smaller, or the same as in the original two-block system. Explain how you arrived at your answer.
▶️Answer/Explanation
Ans:
(a) 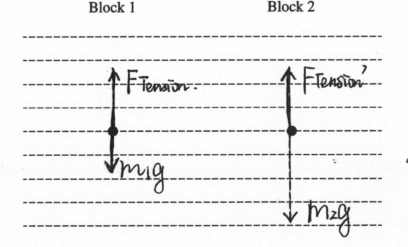
(b) According to Newton’s Second Law
For block 2: m2g – FT’ = m2.a
For block 1: Ft – m1g = m1.a.
According to Newton’s 3rd Law = |FT| = |FT’|
∴ m2g – m1g = m2a + m1a.
∴\(a^{2}=\frac{\left ( m_{2}-m_{1} \right )g}{m_{1}+m_{2}}\)
(c) a2 = a system = \(\frac{\left ( m_{2}-m_{1} \right )g}{m_{1}+m_{2}+m_{3}}< \frac{\left ( m_{2}-m_{1} \right )g}{m_{1}+m_{2}}=a_{2} original\)
∴ the acceleration now is smaller than that before due to the increase in the total mass of the system.
