Question
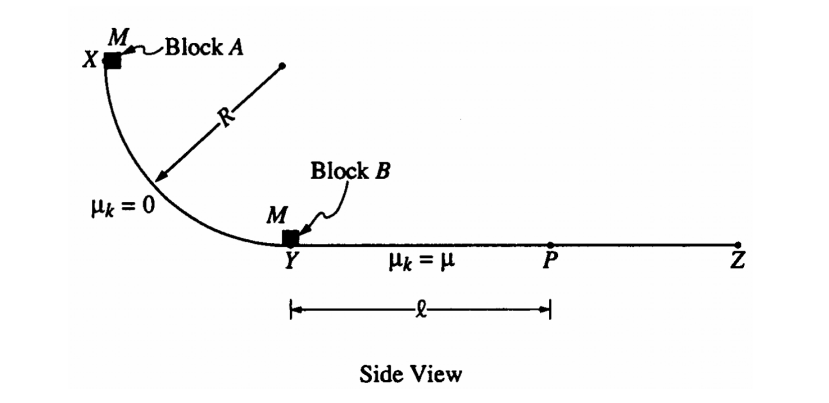
A track consists of a frictionless arc XY, which is a quarter-circle of radius R, and a rough horizontal section YZ. Block A of mass M is released from rest at point X, slides down the curved section of the track, and collides instantaneously and inelastically with identical block B at point Y. The two blocks move together to the right, sliding past point P, which is a distance L from point Y. The coefficient of kinetic friction between the blocks and the horizontal part of the track is μ Express your answers in terms of M, L, μ, R, and g.
a. Determine the speed of block A just before it hits block B.
b. Determine the speed of the combined blocks immediately after the collision.
c. Assuming that no energy is transferred to the track or to the air surrounding the blocks. Determine the amount of internal energy transferred in the collision
d. Determine the additional thermal energy that is generated as the blocks move from Y to P
▶️Answer/Explanation
Ans:
a) Apply energy conservation top to bottom. U = K mgh = ½ mv2 (gR) = ½ v2 v = \(\sqrt{2gR}\)
b) Apply momentum conservation
pbefore = pafter mavai = (ma+mb)vf \(M\sqrt{2gR} = 2Mv_{f}\) \(v_{f} = \frac{\sqrt{2gR}}{2}\)
c) The loss of the kinetic energy is equal to the amount of internal energy transferred
∆K = Kf – Ki = ½ 2M \(\left ( \frac{\sqrt{2gR}}{2} \right )^{2}\) – ½ M \(\left ( \sqrt{2gR} \right )^{2}\) = – MgR / 2 lost → MgR / 2 internal energy gain.
d) Find the remaining kinetic energy loss using work-energy theorem which will be equal the internal energy gain.
Wnc = ∆K – fkd = – μFnd = – μ(2m)gL = –2 μMgL, kinetic loss = internal E gain → 2μMgL
Question
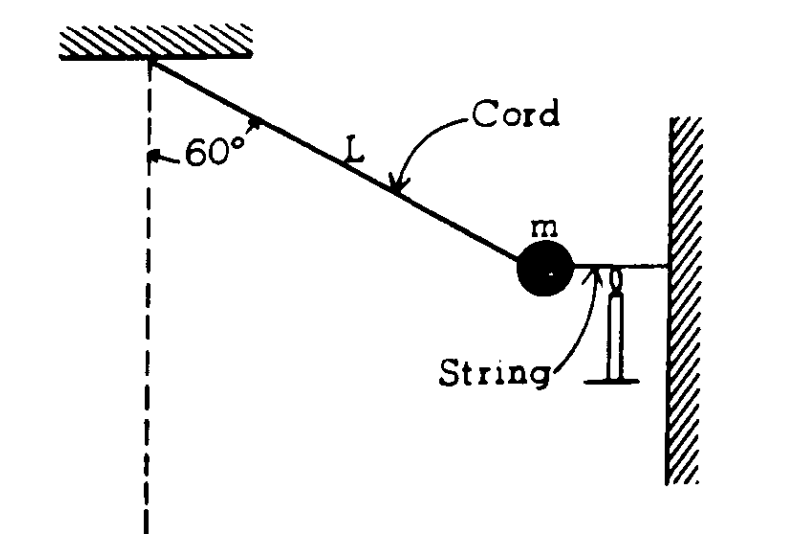
A pendulum consists of a small object of mass m fastened to the end of an inextensible cord of length L. Initially, the pendulum is drawn aside through an angle of 60° with the vertical and held by a horizontal string as shown in the diagram above. This string is burned so that the pendulum is released to swing to and fro.
a. In the space below draw a force diagram identifying all of the forces acting on the object while it is held by the string.

b. Determine the tension in the cord before the string is burned.
c. Show that the cord, strong enough to support the object before the string is burned, is also strong enough to support the object as it passes through the bottom of its swing.
▶️Answer/Explanation
Ans:
(a) 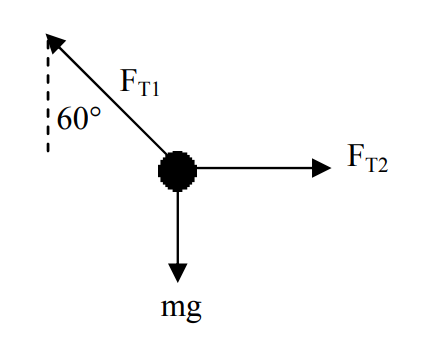
(b) FNET(Y) = 0
FT1 cos θ = mg
FT1 = mg / cos(60) = 2mg
(c) When string is cut it swing from top to bottom, similar to diagram for 1974B1 with θ moved as shown below
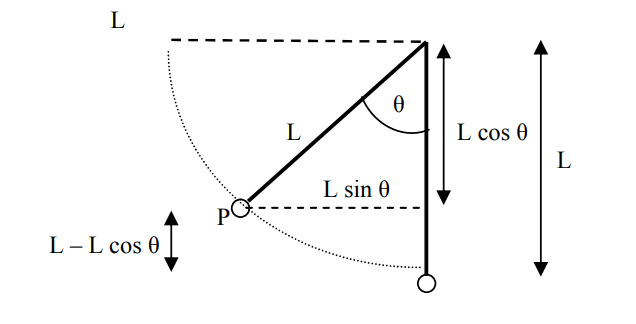
Utop = Kbot
mgh = ½ mv2 Then apply FNET(C) = mv2/ r
\(v = \sqrt{2g (L- L cos 60)}\)
\(v = \sqrt{2g (L-\frac{L}{2})}\) (FT1 – mg) = m(gL) / L
\(v = \sqrt{gL }\) FT1 = 2mg. Since it’s the same force as before, it will be possible.
Question
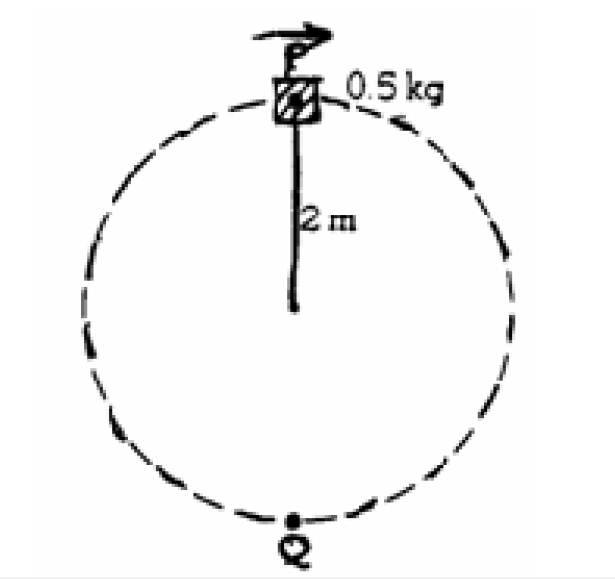
A 0.5 kilogram object rotates freely in a vertical circle at the end of a string of length 2 meters as shown above. As the object passes through point P at the top of the circular path, the tension in the string is 20 newtons. Assume g = 10 meters per second squared.
(a) On the following diagram of the object, draw and clearly label all significant forces on the object when it is at the point P.
![]()
(b) Calculate the speed of the object at point P.
(c) Calculate the increase in kinetic energy of the object as it moves from point P to point Q.
(d) Calculate the tension in the string as the object passes through point Q.
▶️Answer/Explanation
Ans:
(a) 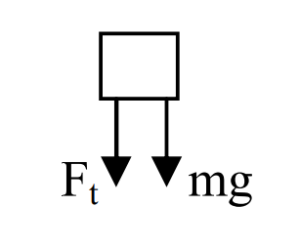
(b) Apply Fnet(C) = mv2/ r … towards center as + direction
(Ft + mg) = mv2/r (20+0.5(10))=(0.5)v2/ 2 v = 10 m/s
(c) As the object moves from P to Q, it loses U and gains K. The gain in K is equal to the loss in U.
∆U = mg∆h = (0.5)(10)(4) = 20 J
(d) First determine the speed at the bottom using energy.
Ktop + Kgain = Kbottom ½ mvtop2 + 20 J = ½ mvbot2 vbot = 13.42 m/s
At the bottom, Ft acts up (towards center) and mg acts down (away from center)
Apply Fnet(C) = mv2/ r … towards center as + direction
(Ft – mg) = mv2/r (Ft – 0.5(10)) = (0.5)(13.42)2/ 2 Ft = 50 N