Question
A 1,500-kilogram car has a velocity of 25 meters per second. If it is brought to a stop by a nonconstant force in 10 to 15 seconds, can the magnitude of the impulse applied be determined?
(A) Yes, it is 37, 500 N · s.
(B) No, you need to know the details about the nonconstant force.
(C) No, you must know the exact duration of the impulse.
(D) No, you must know the average force during and the duration of the impulse.
▶️Answer/Explanation
Ans:(A) Impulse can be found by Ft if the details of the force are known or, alternatively, by:
Impulse = Δp = (1, 500 kg) (0 m/s − 25 m/s) = –37, 500 N•s
Ignore the minus sign as the question asks about magnitude.
Question
This graph of force versus time shows how the force acts on an object of mass m for a total time of T seconds. If the mass begins at rest, which is the correct method to find the final speed of the mass?
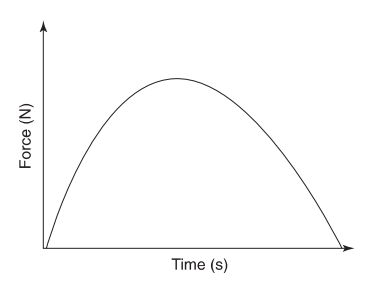
(A) Average value of this graph times total time divided by mass
(B) Area under this graph divided by mass
(C) Since the final force is zero, the object is at rest after time T
(D) Average slope of this graph divided by mass
▶️Answer/Explanation
Ans:(B) Impulse = area of F vs T graph = Δp = mvf − 0
Solving for vf= (area under graph)/m
Question
A 200-kilogram cart rests on top of a frictionless hill as shown below. Can the impulse required to stop the cart when it is at the top of the 10-meter hill be calculated?
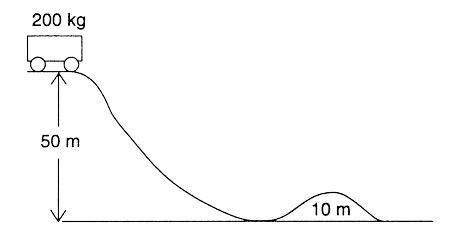
(A) No, more information about friction is required.
(B) No, more information about the impulse is required.
(C) Yes, calculate the velocity from free-fall kinematics and use this velocity in the change in momentum equation.
(D) Yes, calculate the speed from energy conservation and use this speed in the change in momentum equation.
▶️Answer/Explanation
Ans:(D) Conservation of energy while on the frictionless hills can give the speed at the top of the hill:
\(\frac{1}{2}mv^{2}=KE=mg\Delta h\)
Question
Consider the impulse received by the first car in each of the following cases. In each case, the cars are at rest after the collision. In which two of the following cases will the car receive the same impulse? Select two answers.
(A) A 5,000 kg car traveling at 10 m/s has a head-on collision with an equal and oppositely directed second car.
(B) A 5,000 kg car traveling at 10 m/s has a head-on collision with a large building.
(C) A 2,500 kg car traveling at 10 m/s has a head-on collision with an equal and oppositely directed second car.
(D) A 2,500 kg car traveling at 5 m/s has a head-on collision with an equal and oppositely directed second car.
▶️Answer/Explanation
Ans:(A) and (B)
The cars will both experience an impulse of 50,000 N · s. The other two cases result in smaller impulses.
Question
A ball with a mass of 0.2 kilogram strikes a wall with a velocity of 3 meters per second. It bounces straight back with a velocity of 1 meter per second. What was the magnitude of the impulse delivered to this ball?
(A) 0.2 kg · m/s
(B) 0.4 kg · m/s
(C) 0.6 kg · m/s
(D) 0.8 kg · m/s
▶️Answer/Explanation
Ans:(D) Impulse = \(\Delta p=p_{f}-p_{i}=0.2(-1)-(0.2)(3)=\) − 0.8 kg · m/s
