Question
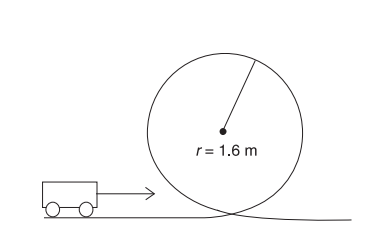
A cart with a mass of m needs to complete a loop-the-loop of radius r , as shown above. What is the approximate minimum velocity required to achieve this goal?
(A) ( gr ) ½
(B) (5 gr ) ½
(C) 2( gr ) ½
(D) (2 gr ) ½
▶️Answer/Explanation
Ans:(B) Circular motion at the top:
Fnet = mg + N = mv2/ r
The lowest speed will be when there is no normal force ( N = 0):
mg = mv2/ r
vtop = ( gr ) ½
KE at the bottom must give both this speed and PE to gain 2 r in height:
Ebottom = Etop
\(\frac{1}{2}mv^{2}=gm(2r)+\frac{1}{2}mv_{top}^{2}\)
\(\frac{1}{2}mv^{2}=gm(2r)+\frac{1}{2}m(gr)\)
Solving for v :
\(v=(5gr)^{1/2}\)
Question
If an object is spinning at 150 RPM (revolutions per minute) and comes to stop in 2 seconds, what is its average acceleration in radians/s 2?
(A) –2.5 π
(B) –2 π
(C) –5 π
(D) –10 π
▶️Answer/Explanation
Ans: (A) First, convert RPMs to rad/s:
150 rev/min × (2 π /1 rev) × (1 min/60 s) = 5 π rad/s
acceleration = change in velocity/time = (0 − 5 π rad/s)/(2 s)
–2.5 π rad/s 2
Question
A conical pendulum consists of a mass m attached to a light string of length L . The mass swings around in a horizontal circle, making an angle θ with the vertical as shown above. What is the magnitude of tension, T , in the string?
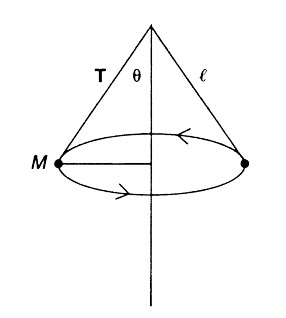
(A) \(mg/cos\Theta\)
(B) \(mg cos\Theta\)
(C) \(mg/sin\Theta\)
(D) \(mg sin\Theta\)
▶️Answer/Explanation
Ans:
(A) Vertical forces must cancel:
\(T\cos\Theta-mg=0\)
\(T=mg/cos\Theta\)
Question
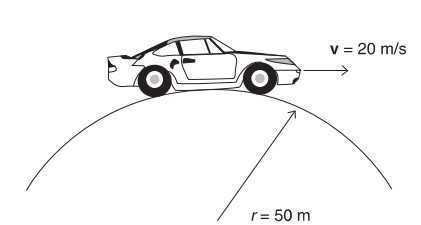
A car with a 500-newton driver goes over a hill that has a radius of 50 meters as shown above. The velocity of the car is 20 meters per second. What are the approximate force and the direction that the car exerts on the driver?
(A) 900 N, up
(B) 400 N, down
(C) 100 N, up
(D) 500 N, up
▶️Answer/Explanation
Ans:(C)
Circular motion: \( F_{net}=mv^{2}/R\)
\(mg-N=mv^{2}/R\)
N is the force the car exerts on the driver: \(mg=mv^{2}/R=(500-50)(20^{2})/50=500-400=100N\)
Note that the correct answer can be found by simply knowing that the net force must be down and that the car must be pushing upward on the passenger.
Question
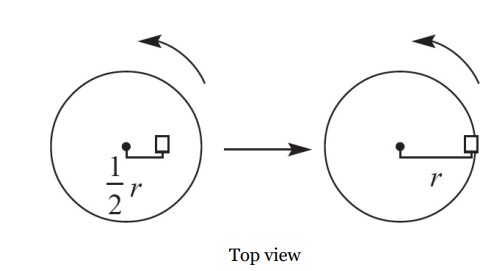
An object is resting on a platform that rotates at a constant speed. At first, it is a distance of half the platform’s radius from the center. If the object is moved to the edge of the platform, what happens to the centripetal force that it experiences? Assume the platform continues rotating at the same speed.
(A) Increases by a factor of 4
(B) Increases by a factor of 2
(C) Decreases by a factor of 2
(D) Decreases by a factor of 4
▶️Answer/Explanation
Ans:B
The formula for centripetal force is \(F_{c}=mv^{2}/r\), which initially seems to indicate the force is inversely proportional to the radius. However, in the case of circular motion, an object’s linear speed is \(v=\omega r\). Substituting this value into the equation gives \(F_{c}=m(\omega r)^{2}/r\). So it turns out that the force is directly proportional to r, which means doubling the radius will double the force on the object.
