Question
An ideal gas expands from points A to C along three possible paths.
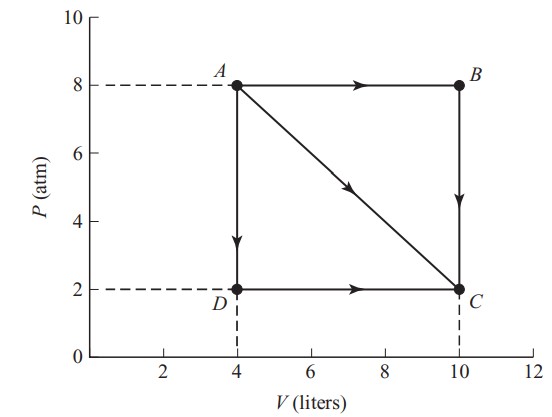
(a) Is it expected that final temperature at point C be path dependent? Justify your answer qualitatively with no calculations.
(b) Discuss and compare the flow of thermal energy along the three paths ( AC , ABC , ADC ). Indicate the direction of heat for each pathway (into or out of the gas) and the relative amount of thermal energy involved. Justify your answer qualitatively with no calculations.
(c) Calculate the work done along path:
i. ABC
ii. AC
iii. ADC
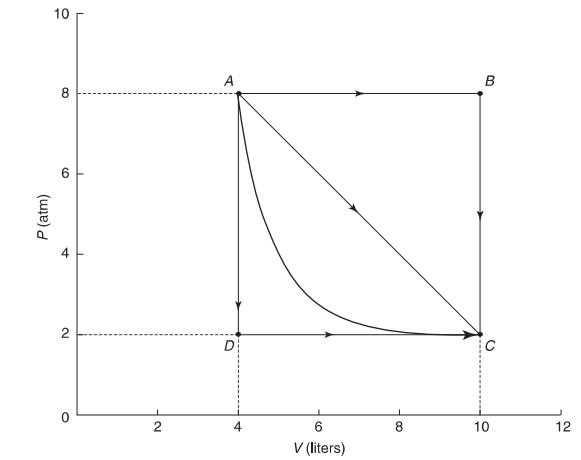
(d) Is there a way to go from A to C with no thermal energy exchanged with the environment? If so, describe and sketch the path on a P – V diagram.
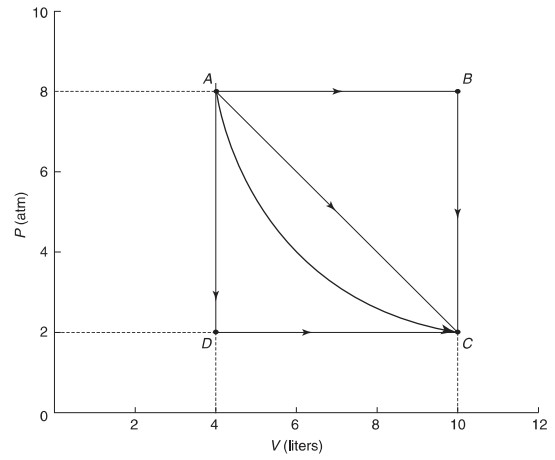
(e) Is there a way to go from A to C with no temperature change? If so, describe and sketch the path on a P – V diagram.
▶️Answer/Explanation
Ans:
(a) No, the temperature is a state function of pressure and volume. So the temperature at point C is not path dependent.
(b) ΔU = Q + W
For an ideal gas, the change in internal energy ( ΔU) is fixed by the change in the temperature. So the difference in thermal energy exchange ( Q ) will be dictated by the amount of work done on each path (see part (c) for a calculation of work). Without doing a calculation, we can visually tell which path is doing more work by examining the areas under the pathways. The product PV is lower at point C than at point A . Therefore, we can conclude that the temperature is lower at point C (ideal gas law PV = nRT ). Since the temperature is decreasing, ΔU is negative while all the work done by the gas represents a loss of energy as well. The difference between the given pathway and an adiabatic expansion (see answer (d)) represents the amount of thermal energy exchanged with the environment ( Q ).
Path AC represents moderate work done by the gas, requiring some thermal energy to be added to the gas during the process but not as much as path ABC , which represents the most work done by the gas. Since pathway ABC is so far from adiabatic, it will require significant thermal energy to be added to the gas. Finally, path ADC is the least amount of work done and the only pathway to require thermal energy to be given to the environment from the gas.
(c) The work done is going to be equal to the area under each segment of the P – V graph. Also recall that 1 atm = 101 kPa = 101,000 N/\(m^{2}\) and 1 L = 0.001 \(m^{3}\):
Pa · \(m^{3}\) = J
i. Along path ABC , no work is done from B → C because there is no change in volume. Thus the area is just the area under AB = (8 atm)(6 L) = 4,848 J.
ii. Along path AC , the total area is equal to:
\(\frac{1}{2}(6atm)(6L)+(2atm)(6L)=3,030J\)
iii. Along path ADC , no work is done from A → D because there is no change in volume. Thus the area is just the area under DC :
(2 atm)(6 L) = 1,212 J
(d) Yes, if the expansion is adiabatic, you can go from A to C with no thermal energy exchanged. This would connect point A and point C with a steep hyperbola. In this case, the work done is solely responsible for the change in internal energy as no heat is involved.
(e) Yes, if the expansion is isothermal, you can go from A to C with no temperature change, In this case, thermal energy will have to be added to the system at the same rate as work is being done by the gas in order to effect no ΔU, This would connect point A and point C with a hyperbola but one less steep than in part (d).
Question
An air bubble is formed at the bottom of a swimming pool and then released. The air bubble ascends toward the surface of the pool.
(A) In a clear, coherent, paragraph-length response, describe any changes in the bubble size and describe the motion of the bubble as it ascends to the surface. Explain the factors that affect the size of the bubble and the bubble’s motion. Include a description of any forces acting on the bubble from the time it is at the bottom of the pool until the bubble is just below the surface of the pool.
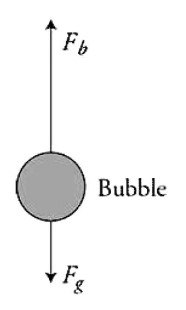
(B) On the figure, draw a vector for each force acting on the bubble. Make sure all vectors are drawn in correct proportion to each other.

(C) The bubble does not collapse under the pressure of the water. Explain how the behavior of the gas atoms keeps the bubble from collapsing.
(D) The bubble begins at a depth of D below the surface of the water where the bubble has an initial volume of \(V_{D}\). The atmospheric pressure at the surface of the pool is \(\rho\). The density of the water in the pool is \(P_{S}\). Assume that the air temperature in the bubble remains constant as it rises to the surface. Derive an expression for the volume (\(V_{S}\)) of the bubble when it reaches the surface of the pool.
(E) In part (D) it was assumed that the temperature of the bubble remains constant. Now assume that the air temperature in the bubble can change but that the bubble rises so quickly to the surface that there is negligible thermal energy transfer between the bubble and the swimming pool water. Base your answers on this assumption.
I. Sketch the process on the PV diagram. Indicate on the axis the initial and final pressures and volumes.
II. How does the value \(P_{S}V_{S}\) compare to the value \(P_{D}V_{D}\)?
_Greater than \(P_{D}V_{D}\) _Equal to \(P_{D}V_{D}\) _Less than \(P_{D}V_{D}\)
Justify your answer.
▶️Answer/Explanation
Ans:
Part (A)
The amount of air inside the bubble remains the same during ascent. The external pressure from the water on the bubble decreases as the
bubble rises. The bubble increases in volume as it moves upward. As the bubble volume increases, the buoyancy force increases, but the gravity force on the bubble remains constant. The bubble accelerates upward at an increasing rate as it ascends.
Part (B)
For buoyancy force upward and gravity force downward. Buoyancy must be drawn larger than gravity. If extra vectors are drawn, this point is not awarded.
Part (C)
The atoms inside the gas collide with and bounce off the water molecules. This causes a change in momentum of the gas atoms. This generates an equal and opposite force between the water and gas that keeps the bubble from collapsing.
Part (D)
For the correct relationship between the pressure at the surface of the water and at a depth D: \(P_{D}=P_{S}+\rho gD\)
For the correct application of the ideal gas law and the correct final expression:
\(P_{S}V_{S}=P_{D}V_{D}\)
\(P_{S}V_{S}=(P_{S}+\rho gD)V_{D}\)
\(V_{S}=\frac{(P_{S}+\rho gD)V_{D}}{P_{S}})
Part (E)
(i) 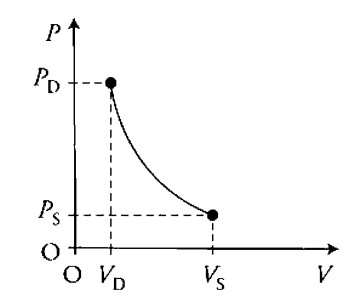
(ii) The process is an adiabatic expansion. There is no heat transfer between the water and the bubble. Therefore: \(Q=0\), and \(\Delta U=W\). Since the work is negative as the bubble expands, the internal energy of the bubble must also decrease. Therefore, the temperature and the PV value must also decrease.
Question
A cylinder, with a sealed movable piston, is filled with a gas and sits on a lab station table in thermal equilibrium with the lab room. The original pressure, volume, and temperature of the gas are \(P_{0}\), \(V_{0}\), and \(T_{0}\), respectively. You have been instructed by the teacher to experimentally determine the work required to compress the gas to half its original volume.
(A) Describe an experimental procedure you could use to determine the work. Include the following:
• all the equipment needed
• a labeled diagram of the setup
• a clear indication of which variables will be manipulated and which will be measured
• a clear explanation of how the work will be calculated from your data
• enough detail so that another student could carry out the procedure
While performing the experiment, your lab partner makes this claim: “If we compress the gas very slowly, the gas will have a lower final temperature than if we compress the gas very quickly. But, the work will be the same in either case, so it doesn’t matter which way we do it.”
(B) Which parts, if any, of your lab partner’s claim are correct? Justify your response.
(C) Which parts, if any, of your lab partner’s claim are incorrect? Justify your response.
(D) On the graph, sketch the pressure as a function of volume as the gas is compressed from its original pressure PO and volume V0 (shown by a dot on the graph) to half its original volume. Assume that the gas remains in thermal equilibrium with the lab room throughout the compression.
(E) Utilizing your answer from (D), explain how the graph could be utilized to find the work required to compress the gas.
▶️Answer/Explanation
Ans:
Part (A)
There is more than one way to accomplish this lab. Here are two possibilities:
Method #1
Choose a force sensor and a ruler.
Force will be manipulated by pushing down on the piston with the force sensor, and the distance the gas in the cylinder is compressed will be measured.
Labeled diagram that shows the piston, how the force will be measured, and how the distance the gas is compressed will be measured.
Work will be calculated by using Y= Fix — area under the graph of force versus distance the gas is compressed.
Procedure: Cylinder is placed vertically on the lab table. Force sensor is used to push the piston down in 0.01-m increments until we have reached half the original volume. Force and distance compressed are recorded for each. Plot force as a function of distance compressed on a graph. The work will equal the area under the graph.
Method #2
Choose a pressure sensor and a ruler.
The pressure is manipulated and the distance the gas in the cylinder is compressed will be measured.
Labeled diagram that shows the piston, how the force will be applied and the pressure is measured, how compression distance will be measured.
Work is calculated using: Y= PMV — area under the graph of pressure versus volume of gas inside the cylinder.
Procedure: Cylinder is placed vertically on the lab table. Push the piston down in 0.01-m increments until we have reached half the original volume. Pressure and height of the cylinder are recorded for each increment. Calculate volume using K= (area of piston)(height of gas). Plot pressure as a function of volume on a graph. The work will equal the area under the graph.
Note: As the gas is compressed, the pressure inside the gas does not remain constant. The third and fourth points are not awarded unless the student demonstrates an acceptable method for taking this into account while calculating the work. Here are two possible methods a student could use:
• Calculating work by using the area under the F versus x graph or P versus K graph
• A student could state that the force/pressure is not constant and that they will estimate an average force/pressure.
Part (B)
Correct statement: The temperatures will be different depending on the speed of compression.
Justification: When compressing the gas very slowly, heat has time to escape, lowering the final temperature. If the compression is done quickly, there is no time for heat to escape and the final temperature will be higher.
Part (C)
Incorrect statement: The work will be the same in either case.
Justification: Compressing the gas quickly will not allow time for heat to escape to the environment. This will give the gas a higher final temperature and thus a higher final pressure for the same final volume. This means more force is required to compress the gas quickly and thus more work is required as well.
Part (D)
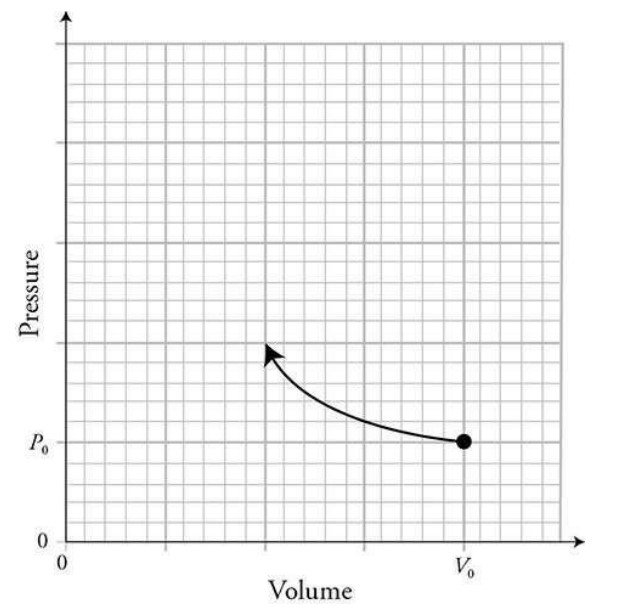
Part (E)
The work would be calculated by finding the area under the sketched line.
