Question
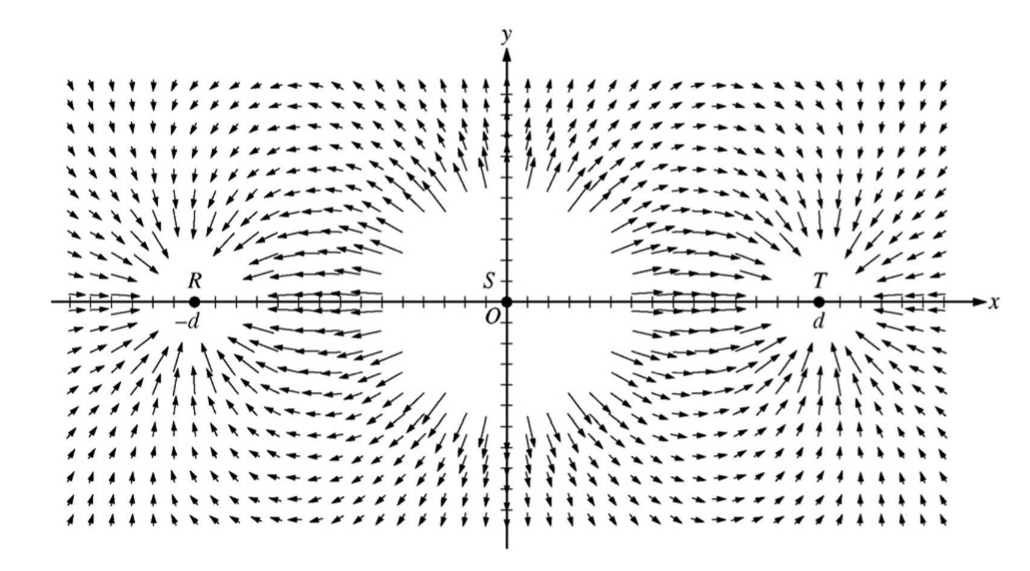
The figure above represents the electric field in the vicinity of three small charged objects, R, S, and T. e objects have charges -q, +2q, and -q , respectively, and are located on the x-axis at -d , 0, and d. Field vectors of very large magnitude are omitted for clarity.
(a)(i) Briefly describe the characteristics of the field diagram that indicate that the sign of the charges of objects R and T is negative and that the sign of the charge of object S is positive.
(ii) Briefly describe the characteristics of the field diagram that indicate that the magnitudes of the charges of objects R and T are equal and that the magnitude of the charge of object S is about twice that of objects R and T.
For the following parts, an electric field directed to the right is defined to be positive.
(b) On the axes below, sketch a graph of the electric field E along the x-axis as a function of position x.
(c) Write an expression for the electric field E along the x-axis as a function of position x in the region between objects S and T in terms of q, d, and fundamental constants, as appropriate.
(d) Your classmate tells you there is a point between S and T where the electric field is zero. Determine whether this statement is true, and explain your reasoning using two of the representations from parts (a), (b), or (c)
▶️Answer/Explanation
Ans:(a)
(i) For indicating that the direction of the field vectors is the telling characteristic and describing how they indicate negative and positive charge
Example: The direction of the field vectors. Field vectors near objects point toward negatively charged objects and away from positively charged objects.
(ii) For indicating that the size and distance of the closest field vectors are the telling characteristics
For describing how the size and distance of the closest field vectors indicate the magnitudes of the charges Field vectors nearest R and T are at about the same distance and have approximately the same length, so the magnitude of their charge is equal. Field vectors nearest S have approximately the same length as field vectors nearest R and T, but the square of the distance to the field vectors nearest S is about twice the square of the distance to the field vectors nearest R and T –36 (6 tic marks squared) compared with 16 (4 tic marks squared). So the
magnitude of the charge of S is twice the magnitude of the charges of R and T.
Example:
The vectors closest to R and T are about the same length and start at about the same distance \( q_R/d^2= q_T/d^2\) ,. so the charge on R is about the same as the charge on T. The closest vectors around S are about the same length as those around R and T. The vectors near S start at about 6 units away, while vectors near R and T start at about 4 units\( q_R/d^2= q_S/D^2\). so ,
\( q_S/q_R=D^2/d^2 \) and so the charge on S is about twice that on R and T.
(b) For showing reasonably close to asymptotic behavior on both sides of the charge positions
For a general U shape between the charges that does not touch the x-axis
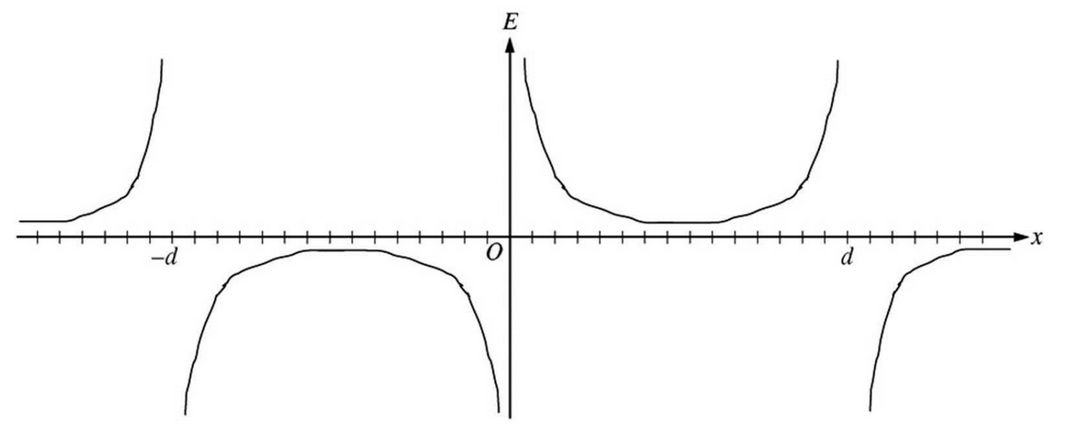
For all signs consistent with the vector map
The following shows a more exact plot. e scale is set to show the asymptotic behavior, which masks the nonzero values between charges and at both sides of the range.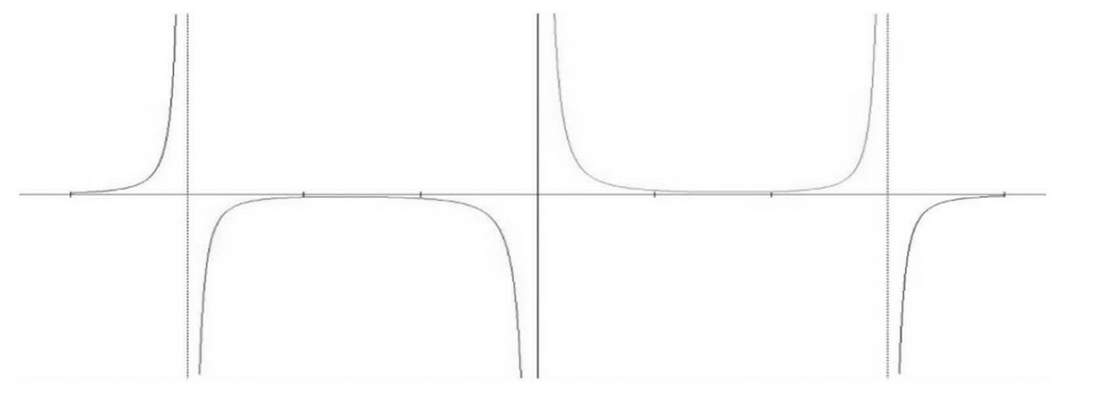
(c) For correctly associating charge values with positions
For using the correct sign and power in the expressions for the distance to each charge , For the correct sign for the direction of the field for each term 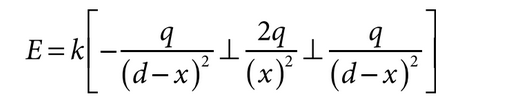
(d) For indicating that the value of the electric field is nonzero for all values between S and T
For justifying the above using one of the representations
For justifying the above using a second representation
The following are the ideas that should be expressed for each representation:
\(\blacksquare \) The vectors between S and T in the electric field diagram all have nonzero length
\(\blacksquare \) The graph between S and T never crosses the x-axis
\(\blacksquare \) The negative term of the equation in part (c) is either always smaller than the other terms in this region or never completely cancels them both
Example:
The statement is not true. e vector diagram shows field vectors in this region with nonzero length, and the vectors not shown have even greater lengths. The equation in part (c) shows that when the denominator of the negative term is always greater than the denominator of the third term, but the numerator is the same. So the negative term always has a smaller magnitude than the third term, and since the second term is positive, the sum of the terms is always positive. Note: A response claiming that there is a zero value can receive credit if it is consistent with an incorrect response in either part (b) or (c).
Question
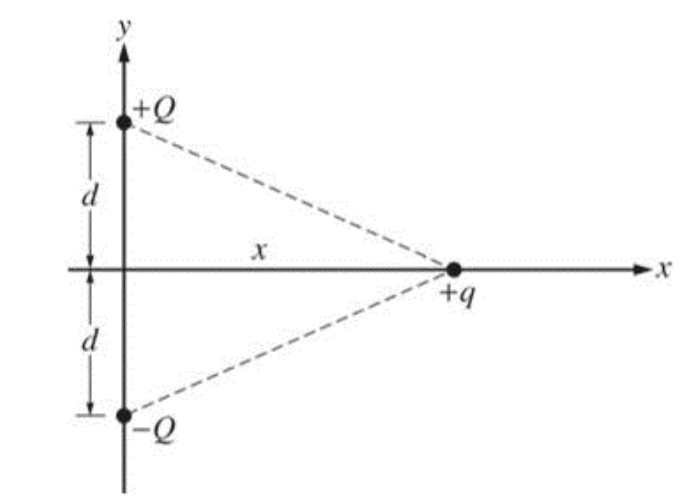
Three electric charges are arranged on an x–y coordinate system, as shown above. Express all algebraic answers to the following parts in terms of Q, q, x, d, and fundamental constants.
a. On the diagram, draw vectors representing the forces F1 and F2 exerted on the +q charge by the +Q and –Q charges, respectively.
b. Determine the magnitude and direction of the total electric force on the +q charge.
c. Determine the electric field (magnitude and direction) at the position of the +q charge due to the other two charges.
d. Calculate the electric potential at the position of the +q charge due to the other two charges.
e. Charge +q is now moved along the positive x–axis to a very large distance from the other two charges.
The magnitude of the force on the +q charge at this large distance now varies as 1/x3. Explain why this happens.
▶️Answer/Explanation
Ans:
a. 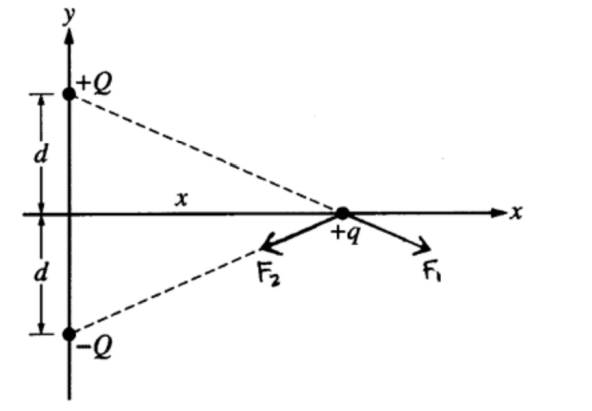
b. The x components of the forces cancel so the net force is the sum of the y components, which are equal in magnitude and direction. Fnet = 2 × F cos θ where θ is the angle between the y axis and the dashed line in the diagram above. cos θ = d/r = \(d/\sqrt{x^{2}+d^{2}}\)
This gives Fnet = 2 × kqQ/r2 × cos θ = 2kqQd/(x2 + d2)3/2
c. E = F/q at the point where q1 lies. E = 2kQd/(x2 + d2)3/2
d. Since the charges Q and –Q are equidistant from the point and V = \(\sum \) kQ/r, the potential V = 0
e. As x gets large, the distance to the charges r and the value of x become similar, that is \(\sqrt{x^{2}+d^{2}}\) ≈ x. Substituting this into the answer to b. yields F = 2kqQd/x3
Question
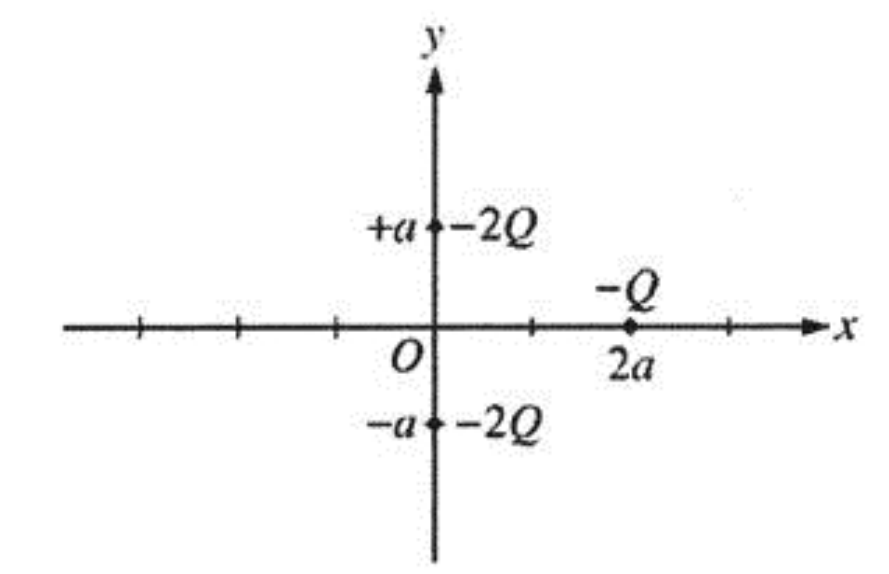
The figure above shows two point charges, each of charge –2Q, fixed on the y–axis at y = +a and at y = –a. A third point charge of charge –Q is placed on the x–axis at x = 2a. Express all algebraic answers in terms of Q, a, and fundamental constants.
a. Derive an expression for the magnitude of the net force on the charge –Q due to the other two charges, and state its direction.
b. Derive an expression for the magnitude of the net electric field at the origin due to all three charges, and state its direction.
c. Derive an expression for the electrical potential at the origin due to all three charges.
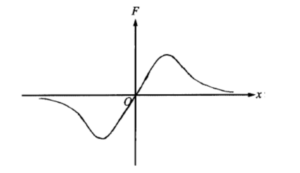
d. On the axes below, sketch a graph of the force F on the –Q charge caused by the other two charges as it is moved along the x–axis from a large positive position to a large negative position. Let the force be positive when it acts to the right and negative when it acts to the left.
▶️Answer/Explanation
Ans:
a. The distance between the charges is r = \(\sqrt{a^{2}+(2a)^{2}} = \sqrt{5a}\) The y components of the forces due to the two –2Q charges cancel so the magnitude of the net force equals the sum of the x components, where Fx = F cos θ and cos θ = 2a/r = 2/√5
Putting this all together gives Fx = 2 × (kQ(2Q)/r2) cos θ = 8kQ2/5√5a2 to the right (+x)
b. The contribution to the field from the –2Q charges cancel. This gives E = kQ/(2a)2 = kQ/4a2 to the right (+x)
c. V = \(\sum \) kQ/r = k(–2Q)/a + k(–2Q)/a + k(–Q)/2a = –9kQ/2a
d. At the origin the force is zero (they cancel). As the charge moves away from the origin, the force first increases as the x components grow, then decrease as the distance grows larger.