QUESTIONS (A)–(C) ARE BASED ON THE FOLLOWING CIRCUIT:
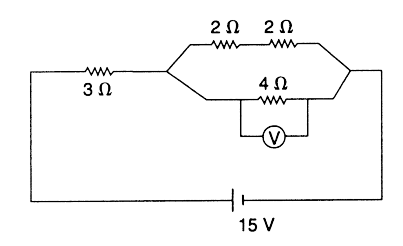
Question(A)
What is the equivalent resistance of the circuit?
(A) 6 Ω
(B) 8 Ω
(C) 11 Ω
(D) 5 Ω
▶️Answer/Explanation
Ans:(D)
The two 2 Ω resistors are in series with each other: 2 Ω + 2 Ω = 4 Ω. This 4 Ω equivalent resistance is in parallel with the existing 4 Ω resistor: ¼ Ω + ¼ Ω = ½ Ω. So the equivalent resistance for that section of the circuit is 2 Ω. This 2 Ω equivalent resistance is in series with the 3 Ω resistor: 2 Ω + 3 Ω = 5 Ω.
Question(B)
What is the reading of the voltmeter across the 4-ohm resistor?
(A) 3 V
(B) 9 V
(C) 12 V
(D) 6 V
▶️Answer/Explanation
Ans:(D) The 15 volts must be split between the 3-ohm resistor and the 2-ohm equivalent resistance of the right-hand side (see answer 23). Voltage for the 4-ohm resistor is the same as the voltage across the 2-ohm equivalent resistance of the right-hand side:
V = (2/5)(15 V) = 6 V
Question(C)
What is the current through the leftmost 2-ohm resistor?
(A) 3 A
(B) 1.5 A
(C) 0.75 A
(D) 1 A
▶️Answer/Explanation
Ans:(B) The 15-volt battery will supply 3 amps of current for the 5-ohm circuit:
V = IR
15 V = (3A)(5 ohm)
This 3-amp current will split as it comes to the branching point before the 4-ohm resistor. Since both pathways have equal resistance (4 ohms), the current will split evenly: 1.5 amps.
Question
A wire segment in a circuit with a cross-sectional area of A and length L is replaced by a wire segment made of the same material that has twice the area but half the length. The resistance of the new segment, compared to the original segment, will
(A) be reduced by half
(B) be reduced to one-quarter
(C) quadruple
(D) remain the same
▶️Answer/Explanation
An(B) Resistance is determined by:
ρL/A
The same material means the resistivity, ρ, is the same. Letting L → L/2 and A → 2A:
ρL/A → ρ(L/2)/(2A) = (ρL/A)/4
Multiple-Correct Items
Directions: Identify exactly two of the four answer choices as correct and grid the answers with a pencil on the answer sheet. No partial credit is awarded; both of the correct choices, and none of the incorrect choices, must be marked for credit.
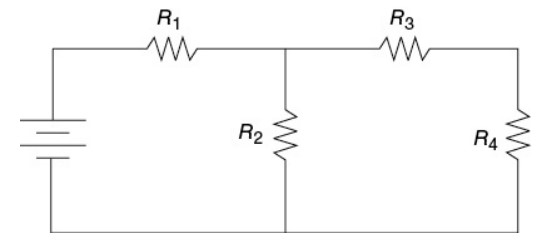
Question
Which placement of voltmeters will allow for determination of the voltage across resistor \(R_{2}\) in the circuit diagrammed in the preceding figure? Select two answers.
(A)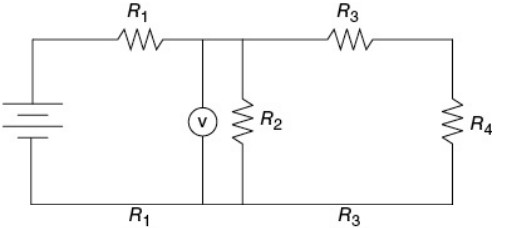
(B) 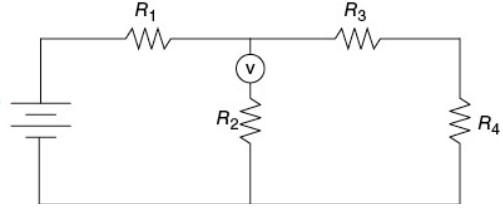
(C) 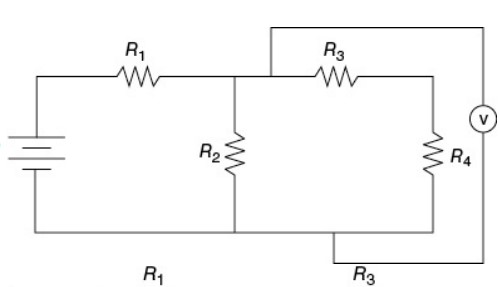
(D) 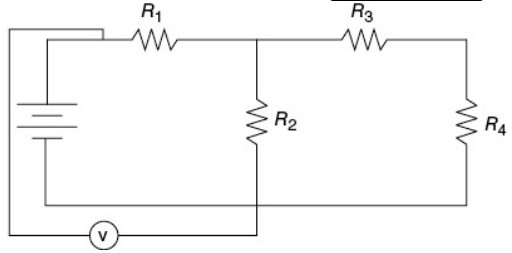
▶️Answer/Explanation
Ans:
A and C—This is essentially Kirchoff’s loop rule, which boils down to “items in parallel take the same voltage.” It’s pretty easy to see that the voltmeter in (A) is in parallel with \(R_{2}\), but in (C) it’s harder. Note that the current must divide between \(R_{2}\) and the voltmeter, and then the current comes immediately back together after going through the voltmeter and \(R_{2}\). That’s parallel. \(R_{3}\) and \(R_{4}\) are also in parallel with the voltmeter here, but that’s not relevant to the problem. Choice (B) is wrong because the voltmeter is in series with \(R_{2}\). Choice (D) is wrong because the voltmeter is in parallel with the battery, which is not in parallel with \(R_{2}\), because \(R_{1}\) is in the way.
