Question
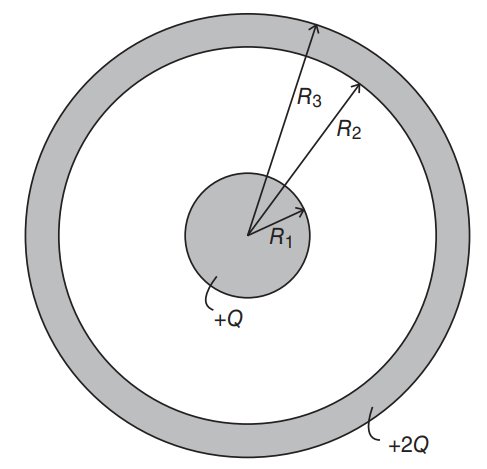
A metal sphere of radius R1 carries charge +Q. A concentric spherical metal shell, of inner radius R2 and outer radius R3, carries charge +2Q.
(a) Let r represent the distance from the center of the spheres. Calculate the electric field as a function ofr in each of the following four regions:
1. between r = 0 and r = R1
2. between r = R1 and r = R2
3. between r = R2 and r = R3
4. between r = R3 and r = 0
(b) How much charge is on each surface of the outer spherical shell? Justify your answer.
(c) Determine the electric potential of the outer spherical shell.
(d) Determine the electric potential of the inner metal sphere.
Answer/Explanation
Ans:(a)
Inside a conductor, the electric field must always be zero. E = 0. Because we have spherical symmetry, use Gauss’s law. The area of a Gaussian surface in this region is \(4\pi r^2\). The charge enclosed by this surface is Q.
So, \(E = Q_{enclosed}/\varepsilon _{0}A = Q/4\pi \varepsilon _{0}r^2\)
Inside a conductor, the electric field must always be zero. E = 0. Just as in part 2, use Gauss’s law, but now the charge enclosed is 3Q. \(E = 3Q/4\pi \varepsilon _{0}r^2\)
(b)
−Q is on the inner surface. +3Q is on the outer surface. Because E = 0 inside the outer shell, a Gaussian surface inside this shell must enclose zero charge, so −Q must be on the inside surface to cancel the +Q on the small sphere. Then to keep the total charge of the shell equal to +2Q, +3Q must go to the outer surface.
(c)
Because we have spherical symmetry, the potential due to both spheres is \(3Q/4\pi \varepsilon _{0}r^2\), with potential equal to zero an infinite distance away. So at position \(R_3\) , the potential is \(3Q/4\pi \varepsilon _{0}R_3\). (Since E = 0 inside the shell, V is the same value everywhere in the shell.)
(d) Integrate the electric field between \(R_1\) and \(R_2\) to get \(V = Q/4\pi \varepsilon _{0} r+ a\) constant of integration.
To find that constant, we know that \(V(R_2)\)was found in part (c), and is \(3Q/4\pi \varepsilon _{0}R_3\). Thus, the constant is
\(\frac{3Q}{4\pi \varepsilon _{0}R_3}- \frac{Q}{4\pi \varepsilon _{0}R_2}\)
