Question
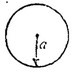
The isolated conducting solid sphere of radius a shown above is charged to a potential V.
a. Determine the charge on the sphere.
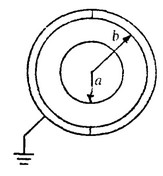
Two conducting hemispherical shells of inner radius b are then brought up and, without contacting the
solid sphere are connected to form a spherical shell surrounding and concentric with the solid sphere as
shown below The outer shell is then grounded.
b. By means of Gauss’s law, determine the electric field in the space between the solid sphere and the
shell at a distance r from the center.
c. Determine the potential of the solid sphere relative to ground.
d. Determine the capacitance of the system in terms of the given quantities and fundamental constants.
Answer/Explanation
Ans:
a. V = kQ/a so Q = aV/k
b. \(\oint E.dA = \frac{Q_{enc}}{\varepsilon _0}\)
\(E(4 \pi r^2) = Q/ \varepsilon_0\)
\(E = aVr^2\)
c.
\(\Delta =-\int E.dr=-\int_{b}^{a}E.dr=- \int_{b}^{a}\frac{kQ}{r^2}dr = kQ(\frac{1}{a}-\frac{1}{b})=\frac{V(b-a)}{b}\)
d. \(Q=C\Delta V\)
aV/k = CV(b-a)/b\)
C = ab/k(b-a)
Question
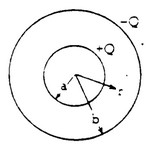
A capacitor is composed of two concentric spherical shells of radii a and b, respectively, that have
equal and opposite charges as shown above. Just outside the surface of the inner shell, the electric field
is directed radially outward and has magnitude \(E_0\).
a. With the use of Gauss’s law, express the charge +Q on the inner shell as a function of \(E_0\) and a.
b. Write an expression for the electric field strength E between the shells as a function of \(E_o\), a, and r.
c. What is the potential difference V between the shells as a function of \(E_0\), a, and b?
d. Express the energy U stored in this capacitor as a function of \(E_o\), a, and b.
e. Determine the value of a that should be chosen in order to maximize U, if \(E_0\) and b are fixed.
Answer/Explanation
Ans:
a. \(\oint E. dA = \frac{Q_{enc}}{\varepsilon_0}\)
\(\varepsilon_o E_o 4 \pi a^2 = Q\)
b. \(E=kQ/r^2 = E_0 a^2/r^2\)
c. \(V=kQ/r\) \(kQ=E_{0a}^2\) \(V(a)=kQ/a\) \(V(b)=kQ/b\)
\(\Delta V = E_0 a^2(1/a-1/b)\)
d. \(U=1/2 Q \Delta V = 2 \pi \varepsilon_0^2(a^3-a^4/b)\)
e. setting \(dU/da=0\) gives \(a=3/4 b\)
Question
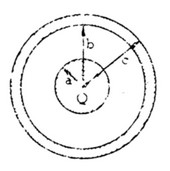
A conducting sphere of radius a and charge Q is surrounded by a concentric conducting shell of
inner radius b and outer radius c as shown above. The outer shell is first grounded; then the grounding
wire is removed.
a. Using Gauss’s law, determine the electric field in the region a < r < b, where r is the distance from the
center of the inner sphere.
b. Develop an expression for the capacitance \(C_o\) of the system of the two spheres.
A liquid dielectric with a dielectric constant of 4 is then inserted in the space between the conducting spheres and the shell, filling half of the space as shown below.
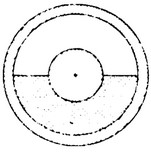
c. Determine the capacitance C of the system in terms of \(C_o\)
Answer/Explanation
Ans:
a. \(\oint E. dA = \frac{Q_{enc}}{\varepsilon_o}\)
\(E(4 \pi r^2)=Q/ \varepsilon_o\)
\(E=Q/4 \pi \varepsilon_o r^2\)
b. \(C=Q/ \Delta V \) where \(\Delta V = kQ/a – kQ/b\) giving \(C_0=4 \pi \varepsilon_0(ab/b-a)\)
c. Consider the system as two capacitors in parallel \(C_{top}=C_o/2\) (half the area) and \(C_{bottom}=kC_0/2=C_0/2 \times 4\)
