Question
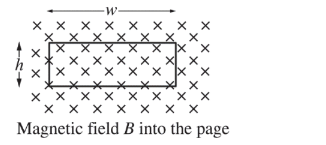
A wire loop with width w and height h is in a magnetic field that is directed into the page, as shown in the figure above. The magnitude B of the magnetic field changes with time t. The magnitude of the resulting induced emf in the wire loop is given as a function of time by the equation\(\varepsilon= \beta h w t^3\), where \(\beta\) is a positive constant in units of \(T /s^4\) . Which of the following is a possible expression for the magnitude of the magnetic field?
(A)\(\frac{1}{4}\beta t^3\)
(B)\(3\beta t^4\)
(C)\(3hw\beta t^4\)
(D)\(\frac{1}{4}hw\beta t^4\)
(E)\(\frac{1}{4}\beta t^4\)
Answer/Explanation
Ans:E
Given the induced emf \(\varepsilon = \beta hwt^3\) and since the equation for emf is \(\varepsilon =-\frac{\phi _B}{dt}\) one can set them equal to each other. The magnetic flux must first be determined through the wire loop. The magnetic flux through this loop is given by \(\phi _B = BAsin(\theta )\), where A is the area of the loop, and the angle is 90 degrees since the magnetic field is perpendicular to the loop. Thus, \(\phi _B = Bwhsin(90) = Bwh\). Thus, by setting the given emf equal to the equation for emf, substituting in the magnetic flux, then integrating with respect to t, and taking the magnitude of the final \(\varepsilon =\varepsilon \)
\( \beta hwt^3=-\frac{\phi _B}{dt}\)
answer results in this option \(\beta hwt^3 dt=-d (Bwh)\)
\(\int B hwt^3dt=\int -d (Bwh)\)
Question
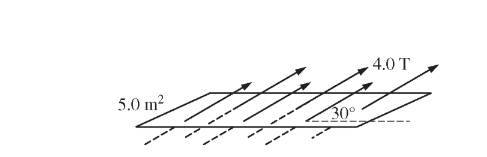
A magnetic field of magnitude 4.0 T is directed at an angle of\( 30^{\circ}\) to the plane of a rectangular loop of area \(5.0 m^2\) , as shown above. What is the magnetic flux through the loop?
(A)\(10T.m^2\)
(B) \(12T.m^2\)
(C) \(17T.m^2\)
(D) \(20T.m^2\)
(E) \(40T.m^2\)
Answer/Explanation
Ans:A
Using the equation for magnetic flux and taking into account the correct angle between a perpendicular vector to the area shown and the magnetic field lines, which would be 60° , the
magnetic flux can be determined by the following calculations.
\(\Phi _m=\int B.dA\)
\(\Phi _m=B.A.cos\Theta\)
\(\Phi _m=(4.0T)(5m^2)(cos(60^{\circ}))\)
Question
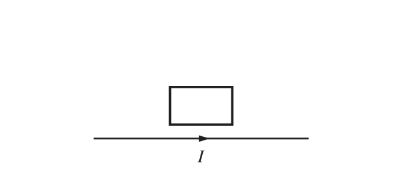
A rectangular conducting loop is located above a long, straight wire carrying a current I to the right, as shown in the figure above. The wire and loop are both in the plane of the page. Which of the following will induce a clockwise current in the loop?
(A) Decreasing the current in the wire
(B) Moving the loop to the right
(C) Moving the loop to the left
(D) Moving the loop up away from the wire
(E) Moving the loop down toward the wire
Answer/Explanation
Ans:E
Using one of the right-hand rules, it can be determined that the magnetic field due to the current-carrying wire it directed out of the page in the loop. Moving the loop closer to the wire will result in
Question
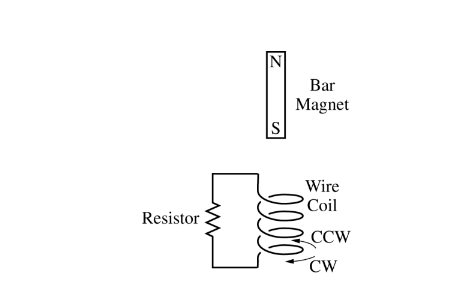
A bar magnet with its south pole pointing down is released from rest and falls through a wire coil, as shown above. A resistor is connected across the two ends of the coil. What current would be produced in the coil, as observed by a person directly above the coil?
(A) A clockwise current only
(B) A counterclockwise current only
(C) A current that is first clockwise and then counterclockwise
(D) A current that is first counterclockwise and then clockwise
(E) No current would be produced.
Answer/Explanation
Question
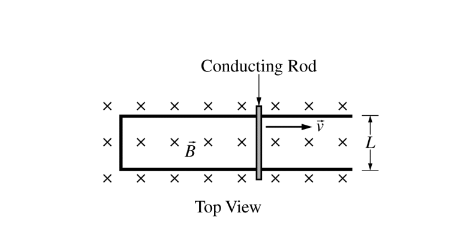
A conducting rod of resistance Ris in electrical contact with a frictionless U-shaped rail of width L and negligible resistance. The rod is pulled to the right at a constant velocity \(\underset{v}{\rightarrow}\). A magnetic field \(\underset{B}{\rightarrow} \)is directed into the page, as shown in the figure above. Under these conditions, the electric power dissipated in the rod is P. If the velocity of the rod is doubled, the power dissipated in the rod is
(A) P/ 4
(B) P/ 2
(C) P
(D) 2P
(E) 4P
