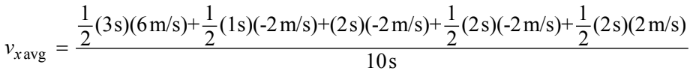Question
An object moves along a straight line with a velocity v given as a function of time t by the equation \(v(t)=\alpha t^2+\beta t+\gamma \)
Which of the following expressions represents Δx (t ) , the displacement of the object as a function of time t starting at time t = 0 ?
(A)\(2\alpha\)
(B)\(\alpha t+\beta\)
(C)\(2\alpha t+\beta\)
(D)\(\alpha t^3/3+\beta t^2/2+\gamma t\)
(E)\(3\alpha t^3+2\beta t^2+\gamma t\)
Answer/Explanation
Question
A cart is moving in the +x-direction and passes the origin when time t= 0. The cart then moves with decreasing speed, stops, and moves in the –x-direction with increasing speed. Which of the following graphs best represents the cart’s position x as a function of time?
Answer/Explanation
Questions(a)-(b)
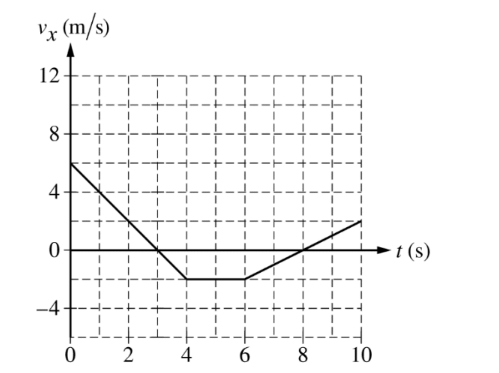
A car moves in a straight line along the x-axis. The velocity of the car vx as a function of time t is shown in the graph above. The position x of the car at t = 0 is x = 0.
Question(a)
The average acceleration \(a_x\) of the car during the interval of 0 to 10 s is most nearly
(A) \( −2.0 m/ s^2\)
(B) \(−0.40 m/ s^2\)
(C)\(+ 0.40 m/ s^2\)
(D) \( +1.0 m/ s^2\)
(E)\(+2.0 m/ s^2\)
Answer/Explanation
Ans:B
The average acceleration is the average rate of velocity change over a time interval. For a velocity-time graph, that will be the slope of the straight line connecting the starting and ending
points. Solving for the slope yields
Question(b)
The average velocity of the car during the interval of 0 to 10 s is most nearly
(A) −1.4 m/ s
(B) +0.40 m/ s
(C) +1.4 m/ s
(D) +1.8 m/ s
(E)+4.0 m /s
Answer/Explanation
Ans:B
By definition, the average velocity is the average rate of position change over an interval. Mathematically, this is \(\frac{\Delta x}{\Delta t}\).Therefore, using the velocity graph’s Δx value, which is the sum of the signed areas under the curve,