Question
A block on a level horizontal surface of negligible friction is initially traveling at 20 m /s to the left. A horizontal force F is exerted to the right on the block for the time interval \(0<t<0.10s\). The magnitude of the force \(\vec{F} \)is given as a function of time t by the equation \(F=\alpha t, where \alpha =240N/s \)and t is in seconds.
What is the magnitude of the change in momentum of the block due to the horizontal force?
(A) 1.2 kg.m s
(B) 12 kg.m s
(C) 24 kg.m s
(D) 240 kg.m s
(E) The change in momentum of the block cannot be determined without knowing the block’s mass.
Answer/Explanation
Question
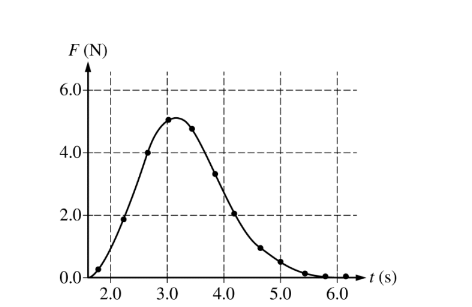
A 300 g cart with a force sensor attached starts at rest on a track. The force sensor exerts a force on the cart to speed it up. The graph above shows the force F exerted by the sensor on the cart as a function of time t. The change in the cart’s momentum during the time interval shown is most nearly
(A) 4.0 N .s
(B) 8.5 N .s
(C) 13 N. s
(D) 25 N .s
(E) 30 N .s
Answer/Explanation
Question
The net force F acting on an object that moves along a straight line is given as a function of time t by \(F (t ) = kt^2 + τ\) , where \( κ = 1 N /s^2\) and τ = 1 N . What is the change in momentum of the object from t = 0 s to t = 3 s?
(A) 6 kg.m/s
(B) 10 kg.m/s
(C) 12 kg.m/s
(D) 30 kg.m/s
(E) It cannot be determined without knowing the initial momentum of the object.
Answer/Explanation
Ans:C
Integrating the equation for the net force and substituting
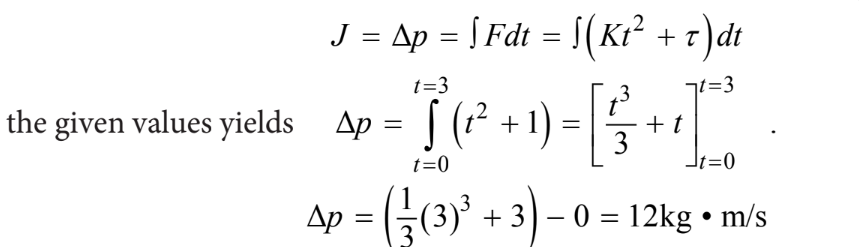
Question
A rubber ball (mass = 0.08 kg) is dropped from a height of 3.2 m and, after bouncing off the floor, rises almost to its original height. If the impact time with the floor is measured to be 0.04 s,
what average force did the floor exert on the ball?
(A) 0.16 N
(B) 16 N
(C) 32 N
(D) 36N
(E) 64N
Answer/Explanation
Ans: C
Because the ball rebounded to the same height from which it was dropped, its takeoff speed from the floor must be the same as the impact speed. Calling up the positive direction,
the change in linear momentum of the ball is \(P_f – P_i = mv – (-mv) = 2mv\), where \(v = \sqrt{2gh}\) (this last equation comes from the equation \(\frac{1}{2}mv^2 = mgh)\). The impulse – momentum theorem, \(J = \Delta p\), now gives
Question
The force on an object as a function of time t is given by the expression \(F=Ct^3\). where C is a constant. Determine the change in momentum for the time interval o to \(t_1\).
(A) \(\frac{Ct_1^2}{2}\)
(B) \(\frac{Ct_1^2}{3}\)
(C) \(\frac{Ct_1^4}{3}\)
(D) \(\frac{Ct_1^4}{4}\)
(E) \(\frac{Ct_1^4}{4}\)
Answer/Explanation
Ans: E
According to the impulse-momentum theorem, the change in momentum of an object is equal to the impulse on an object. The impulse on an object is equal to the integral of F.dt.
