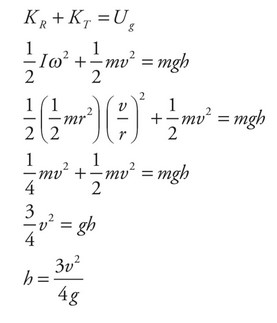Question
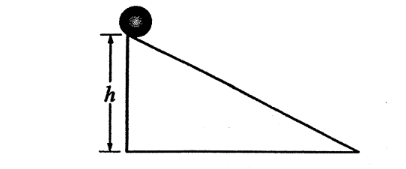
A sphere of mass M, radius r, and rotational inertia I is released from rest at the top of an inclined plane of height h as shown above.
If the plane is frictionless, what is the speed v of the center of mass of the sphere at the bottom of the incline?
(A)\(\sqrt{2gh}\)
(B)\(\frac{2Mgh}{I}\)
(C)\(\frac{2Mghr^2}{I}\)
(D)\(\sqrt{\frac{2Mghr^2}{I}}\)
(E)\(\sqrt{\frac{2Mghr^2}{I+Mr^2}}\)
Answer/Explanation
Question
The radius of a collapsing spinning star (assumed to be a uniform sphere with a constant mass) decreases to \(\frac{1}{16}\) of its initial value. What is the ratio of the final rotational kinetic energy to the initial rotational kinetic energy?
(A) 4
(B) 16
(C) \(16^2\)
(D) \(16^3\)
(E) \(16^4\)
Answer/Explanation
Ans: C
Since no external torques act on the star as it collapses (just like a skater when she pulls in her arms), angular momentum, Iw, is conserved, and the star’s rotational speed
increases. The moment of inertia of a sphere of mass m and radius r is given by the equation \(I = kmr^2 \) (with \(k = \frac{2}{5}\), but the actual value is irrelevant), so we have:
\(\omega _f = \frac{I_i}{I_f} \omega _i = \frac{kmr^2_i}{kmr^2_f}\omega_i = \frac{r^2_i}{r^2_f} \omega _i = \frac{r_i^2}{(\frac{1}{16}r_i)^2} \omega _i = 16^2 \omega_i\)
Therefore,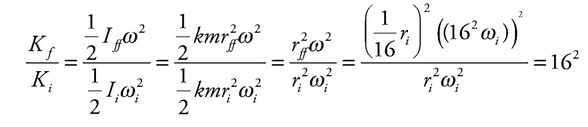
Question
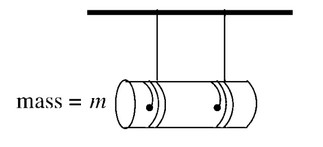
A uniform cylinder of mass m and radius r unrolls without slipping from two strings tied to a vertical support. If the rotational inertia of the cylinder is \(\frac{1}{2} mr^2\) find the acceleration of its center of mass.
(A) \(\frac{1}{4}g\)
(B) \(\frac{1}{2}g\)
(C) \(\frac{1}{3}g\)
(D) \(\frac{2}{3}g\)
(E) \(\frac{3}{4}g\)
Answer/Explanation
Ans: D
Question
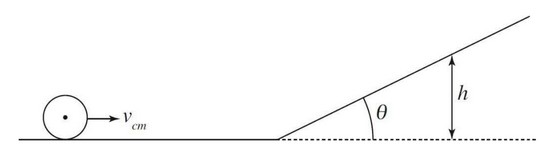
The center of mass of a cylinder of mass m, radius r, and rotational inertia \(I = \frac{1}{2} mr^2\) has a velocity of \(v_{cm}\) as it rolls without slipping along a horizontal surface. It then encounters a ramp of angle \(\theta \), and continues to roll up the ramp without slipping.
What is the maximum height the cylinder reaches ?
(A) \(\frac{v^2}{4g}\)
(B) \(\frac{4v^2}{3g}\)
(C) \(\frac{v^2}{3g}\)
(D) \(\frac{3v^2}{4g}\)
(E) \(\frac{4g}{3v^2}\)
Answer/Explanation
Ans: D
We will use the Law of Conservation of Energy for this problem. The cylinder has rotational and translational kinetic energy as it rolls along the horizontal surface. All of that energy will be converted into gravitational potential energy when it reaches its maximum height up the ramp.