Question
A medical researcher completed a study comparing an omega- 3 fatty acids supplement to a placebo in the treatment of irritability in patients with a certain medical condition. Nineteen patients with the medical condition volunteered to participate in the study. The study was conducted using the following weekly schedule.
- Week 1: Each patient took a randomly assigned treatment, omega-3 supplement or placebo.
- Week 2: The patients did not take either the omega- 3 supplement or the placebo. This was necessary to reduce the possibility of any carryover effect from the assigned treatment taken during week 1 .
- Week 3: Each patient took the treatment, omega-3 supplement or placebo, that they did not take during week 1 .
At the end of week 1 and week 3 , each patient’s irritability was given a score on a scale of 0 to 10 , with 0 representing no irritability and 10 representing the highest level of irritability.
For each patient, the two irritability scores and the difference in their scores (placebo minus omega-3) were recorded. The results are summarized in the table and boxplots.


The researcher claims the omega-3 supplement will decrease the mean irritability score of all patients with the medical condition similar to the volunteers who participated in the study. Is there convincing statistical evidence to support the researcher’s claim at a significance level of \(\alpha=0.05\) ? Complete the appropriate inference procedure to support your answer.
▶️Answer/Explanation
Ans:
(4) \(H_0: \mu_{\text {diff }}=0 \quad \mu_{\text {diff }}=\) true mean difference in irritability \(H_a: M_{\text {diff }}>0 \quad\) scores (place o-Omega 3). for all patients with the medical condition similar to volunteers in the study
One sample t-test for \(M_{\text {diff }}\) (matched pairs + test)
Conditions: – Random: The order of treatments was randomly assigned
– Normal/Large Sample: The boxpot of differences shows no strong skew or outliers
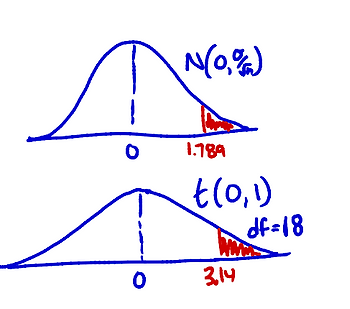
\(\begin{aligned} & \text { standardized }=\frac{\text { statistic }- \text { parameter }}{\text { test statistic }} \\ & t=\frac{\bar{x}_{\text {diff }}-M_{\text {diff }}}{s_{\text {diff }} / \sqrt{n}}=\frac{1.789-0}{2.485 / \sqrt{19}} \\ & t=3.14 \\ & P \text {-value }=0.0028\end{aligned}\)
Because 0.0028<0.05, we reject \(H_0\) and there is convincing evidence that the omega-3 supplement will decrease the mean irritability score of all patients with the medical condition similar to the volunteers that participated in the study.
Question
Researchers studying a pack of gray wolves in North America collected data on the length \(x\), in meters, from nose to tip of tail, and the weight \(y\), in kilograms, of the wolves. A scatterplot of weight versus length revealed a relationship between the two variables described as positive, linear, and strong.
(a) For the situation described above, explain what is meant by each of the following words.
(i) Positive:
(ii) Linear:
(iii) Strong:
The data collected from the wolves were used to create the least-squares equation \(\hat{y}=-16.46+35.02 x\).
(b) Interpret the meaning of the slope of the least-squares regression line in context.
(c) One wolf in the pack with a length of 1.4 meters had a residual of -9.67 kilograms. What was the weight of the wolf?
▶️Answer/Explanation
Ans:
(i) Positive:
Positive means there is a positive correlation between length, in meters, of the wolves and weight, in kilograms, of the wolves. As the length of the wolf increases it is expected that the weight will disc increase.
(ii) Linear
The data follows a linear pattern. As length increases, weight increases. The data points follow approximately the same pattern. Because It is linear we can also assume the residual plot follows ho clear palish.
(iii) Strong:
Strong implies that the data points for each you f are closely related to each other. The points in the scatter plot follow fairly closely to the least squares regression line, also implying that the residuals for the points are small.
(b)As the length of a wolf increases by one meter ( \(x\) variable), the weight of the wolf is predicted to increase by 35.02 kilograms (y variable).
(c) \(\begin{aligned} & -16.46+35.02(1.4 \text { meters })=32.568 \text { kilted } \\ & \begin{aligned} & W-32.568=-9.67 \\ &+ 32.568 \quad+32.568 \\ & W=22.898 \text { kilograms }\end{aligned}\end{aligned}\)