Question
Consider the arithmetic sequence \(u_1\) , \(u_2\) , \(u_3\) , ….
The sum of the first n terms of this sequence is given by \(S_n = n^2 + 4n\).
(a) (i) Find the sum of the first five terms.
(ii) Given that \(S_6\) = 60, find \(u_6\).
(b) Find \(u_1\).
(c) Hence or otherwise, write an expression for \(u_n\) in terms of n.
Consider a geometric sequence, \(v_n\), where \(v_2 = u_1\) and \(v_4 = u_6\).
(d) Find the possible values of the common ratio, r.
(e) Given that \(v_{99} < 0\), find \(v_5\).
Answer/Explanation
Answer:
(a) (i) recognition that n = 5
\(S_5\) = 45
(ii) METHOD 1
recognition that \(S_5 + u_6 = S_6\).
\(u_6\) = 15
METHOD 2
recognition that \(60 = \frac{6}{2} (S_1 + u_6)\)
\(u_6\) = 15
METHOD 3
substituting their \(u_1\) and d values into \(u_1\) + (n – 1)d
\(u_6\) = 15
(b) recognition that \(u_1 = S_1\) (may be seen in (a)) OR substituting their \(u_6\) into \(S_6\)
OR equations for \(S_5\) and \(S_6\) in temrs of \(u_1\) and d
1 + 4 OR 60 = \(\frac{6}{2}\) (\(u_1\) + 15)
\(u_1\) = 5
(c) EITHER
valid attempt to find d (may be seen in (a) or (b))
d = 2
OR
valid attempt to find \(S_n – S_{n-1}\)
\(n^2 + 4n – (n^2 – 2n + 1 + 4n – 4)\)
OR
equating \(n^2 + 4n = \frac{n}{2}(5+u_n)\)
2n + 8 = 5 + \(u_n\) (or equivalent)
THEN
\(u_n\) = 5 + 2(n – 1) OR \(u_n\) = 2n + 3
(d) recognition that \(v_2r^2 = v_4\) OR \((v_3)^2 = v_2 \times v_4\)
\(r^2 = 3\) OR \(v_3 = (±)5\sqrt{3}\)
r = ±\(\sqrt{3}\)
(e) recognition that r is negative
\(v_5\) = -15\(\sqrt{3}\) (=-\(\frac{45}{\sqrt{3}}\))
Question
The nth term of an arithmetic sequence is given by un = 15 – 3n .
(a) State the value of the first term, u1 . [1]
(b) Given that the nth term of this sequence is -33 , find the value of n . [2]
(c) Find the common difference, d . [2]
Answer/Explanation
Ans
(a) \(u_1=12\)
(b) \(15-3n =-33 \therefore n =16\)
(c) valid approach to find d
\(u_2-u_1 = 9-12 =-3\)
\(-33=12+15d\)
or \(d =-3\)
Question
Consider an arithmetic sequence where u8 = S8 = 8 . Find the value of the first term, u1 , and
the value of the common difference, d .
Answer/Explanation
Ans

Question
An arithmetic sequence has \({u_1} = {\text{lo}}{{\text{g}}_c}\left( p \right)\) and \({u_2} = {\text{lo}}{{\text{g}}_c}\left( {pq} \right)\), where \(c > 1\) and \(p,\,\,q > 0\).
a. Show that \(d = {\text{lo}}{{\text{g}}_c}\left( q \right)\).[2]
b. Let \(p = {c^2}\) and \(q = {c^3}\). Find the value of \(\sum\limits_{n = 1}^{20} {{u_n}} \).[6]
Answer/Explanation
a. In arithmetic sequence \({u_2} ={u_1} +d\)
\(u_2 = u_1 +d\)
or
\(d= u_2-u_1\)
\(= log_c(pq)- log_c(p)\)
\(= log_c(p)+log_c(q)- log_c(p)\)
\(=log_c(q)\)
METHOD 1 (finding \({u_1}\) and d)
recognizing \(\sum { = {S_{20}}} \)
attempt to find \({u_1}\) and d using \({\text{lo}}{{\text{g}}_c}\,{c^k} = k\)
eg \({\text{lo}}{{\text{g}}_c}\,c\), \({\text{3}}\,{\text{lo}}{{\text{g}}_c}\,c\), correct value of \({u_1}\) and d
\({u_1}\) = 2, d = 3
We have Sum formula for AP as
\(S_n= \frac{n}{2}(2\times a_1+(n-1)d)\)
hence \({S_{20}} = \frac{{20}}{2}\left( {2 \times 2 + 19 \times 3} \right),\,\,{S_{20}} = \frac{{20}}{2}\left( {2 + 59} \right),\,\,10\left( {61} \right)\)
\(\sum\limits_{n = 1}^{20} {{u_n}} \) = 610
METHOD 2 (expressing S in terms of c)
recognizing \(\sum { = {S_{20}}} \) (seen anywhere) (A1)
correct expression for S in terms of c (A1)
eg \(10\left( {2\,{\text{lo}}{{\text{g}}_c}\,{c^2} + 19\,{\text{lo}}{{\text{g}}_c}\,{c^3}} \right)\)
\({\text{lo}}{{\text{g}}_c}\,{c^2} = 2,\,\,\,{\text{lo}}{{\text{g}}_c}\,{c^3} = 3\) (seen anywhere) (A1)(A1)
correct working (A1)
eg \({S_{20}} = \frac{{20}}{2}\left( {2 \times 2 + 19 \times 3} \right),\,\,{S_{20}} = \frac{{20}}{2}\left( {2 + 59} \right),\,\,10\left( {61} \right)\)
\(\sum\limits_{n = 1}^{20} {{u_n}} \) = 610 A1 N2
METHOD 3 (expressing S in terms of c)
recognizing \(\sum { = {S_{20}}} \) (seen anywhere) (A1)
correct expression for S in terms of c (A1)
eg \(10\left( {2\,{\text{lo}}{{\text{g}}_c}\,{c^2} + 19\,{\text{lo}}{{\text{g}}_c}\,{c^3}} \right)\)
correct application of log law (A1)
eg \(2\,{\text{lo}}{{\text{g}}_c}\,{c^2} = \,\,{\text{lo}}{{\text{g}}_c}\,{c^4},\,\,19\,{\text{lo}}{{\text{g}}_c}\,{c^3} = \,\,{\text{lo}}{{\text{g}}_c}\,{c^{57}},\,\,10\,\left( {{\text{lo}}{{\text{g}}_c}\,{{\left( {{c^2}} \right)}^2} + \,\,{\text{lo}}{{\text{g}}_c}\,{{\left( {{c^3}} \right)}^{19}}} \right),\,\,10\,\left( {{\text{lo}}{{\text{g}}_c}\,{c^4} + \,{\text{lo}}{{\text{g}}_c}\,{c^{57}}} \right),\,\,10\left( {{\text{lo}}{{\text{g}}_c}\,{c^{61}}} \right)\)
correct application of definition of log (A1)
eg \({\text{lo}}{{\text{g}}_c}\,{c^{61}} = 61,\,\,{\text{lo}}{{\text{g}}_c}\,{c^4} = 4,\,\,{\text{lo}}{{\text{g}}_c}\,{c^{57}} = 57\)
correct working (A1)
eg \({S_{20}} = \frac{{20}}{2}\left( {4 + 57} \right),\,\,10\left( {61} \right)\)
\(\sum\limits_{n = 1}^{20} {{u_n}} \) = 610 A1 N2
[6 marks]
Question
Consider the arithmetic sequence \(2{\text{, }}5{\text{, }}8{\text{, }}11{\text{,}} \ldots \) .
Find \({u_{101}}\) .[3]
Consider the arithmetic sequence \(2{\text{, }}5{\text{, }}8{\text{, }}11{\text{,}} \ldots \) .
Find the value of n so that \({u_n} = 152\) .[3]
Answer/Explanation
Markscheme
\(d = 3\) (A1)
evidence of substitution into \({u_n} = a + (n – 1)d\) (M1)
e.g. \({u_{101}} = 2 + 100 \times 3\)
\({u_{101}} = 302\) A1 N3
[3 marks]
correct approach (M1)
e.g. \(152 = 2 + (n – 1) \times 3\)
correct simplification (A1)
e.g. \(150 = (n – 1) \times 3\) , \(50 = n – 1\) , \(152 = – 1 + 3n\)
\(n = 51\) A1 N2
[3 marks]
Question
The sides of a square are 16 cm in length. The midpoints of the sides of this square are joined to form a new square and four triangles (diagram 1). The process is repeated twice, as shown in diagrams 2 and 3.
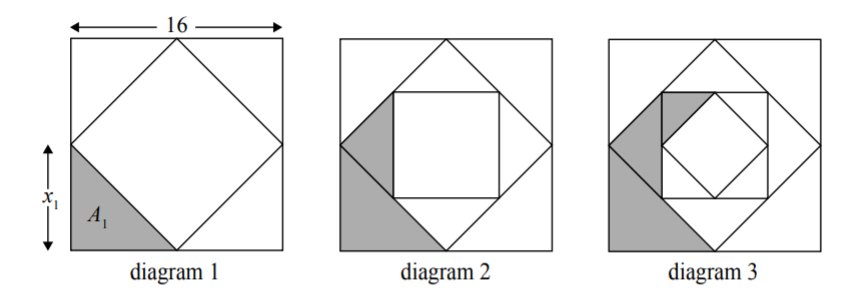
Let \({x_n}\) denote the length of one of the equal sides of each new triangle.
Let \({A_n}\) denote the area of each new triangle.
The following table gives the values of \({x_n}\) and \({A_n}\), for \(1 \leqslant n \leqslant 3\). Copy and complete the table. (Do not write on this page.)
| \(n\) | 1 | 2 | 3 |
| \({x_n}\) | 8 | 4 | |
| \({A_n}\) | 32 | 16 |
The process described above is repeated. Find \({A_6}\).
Consider an initial square of side length \(k {\text{ cm}}\). The process described above is repeated indefinitely. The total area of the shaded regions is \(k {\text{ c}}{{\text{m}}^2}\). Find the value of \(k\).
Answer/Explanation
Markscheme
valid method for finding side length (M1)
eg \({8^2} + {8^2} = {c^2},{\text{ }}45 – 45 – 90{\text{ side ratios, }}8\sqrt 2 ,{\text{ }}\frac{1}{2}{s^2} = 16,{\text{ }}{x^2} + {x^2} = {8^2}\)
correct working for area (A1)
eg \(\frac{1}{2} \times 4 \times 4\)
| \(n\) | 1 | 2 | 3 |
| \({x_n}\) | 8 | \(\sqrt {32}\) | 4 |
| \({A_n}\) | 32 | 16 | 8 |
A1A1 N2N2
[4 marks]
METHOD 1
recognize geometric progression for \({A_n}\) (R1)
eg \({u_n} = {u_1}{r^{n – 1}}\)
\(r = \frac{1}{2}\) (A1)
correct working (A1)
eg \(32{\left( {\frac{1}{2}} \right)^5};{\text{ 4, 2, 1, }}\frac{1}{2},{\text{ }}\frac{1}{4},{\text{ }} \ldots \)
\({A_6} = 1\) A1 N3
METHOD 2
attempt to find \({x_6}\) (M1)
eg \(8{\left( {\frac{1}{{\sqrt 2 }}} \right)^5},{\text{ }}2\sqrt 2 ,{\text{ 2, }}\sqrt 2 ,{\text{ 1, }} \ldots \)
\({x_6} = \sqrt 2 \) (A1)
correct working (A1)
eg \(\frac{1}{2}{\left( {\sqrt 2 } \right)^2}\)
\({A_6} = 1\) A1 N3
[4 marks]
METHOD 1
recognize infinite geometric series (R1)
eg \({S_n} = \frac{a}{{1 – r}},{\text{ }}\left| r \right| < 1\)
area of first triangle in terms of \(k\) (A1)
eg \(\frac{1}{2}{\left( {\frac{k}{2}} \right)^2}\)
attempt to substitute into sum of infinite geometric series (must have \(k\)) (M1)
eg \(\frac{{\frac{1}{2}{{\left( {\frac{k}{2}} \right)}^2}}}{{1 – \frac{1}{2}}},{\text{ }}\frac{k}{{1 – \frac{1}{2}}}\)
correct equation A1
eg \(\frac{{\frac{1}{2}{{\left( {\frac{k}{2}} \right)}^2}}}{{1 – \frac{1}{2}}} = k,{\text{ }}k = \frac{{\frac{{{k^2}}}{8}}}{{\frac{1}{2}}}\)
correct working (A1)
eg \({k^2} = 4k\)
valid attempt to solve their quadratic (M1)
eg \(k(k – 4),{\text{ }}k = 4{\text{ or }}k = 0\)
\(k = 4\) A1 N2
METHOD 2
recognizing that there are four sets of infinitely shaded regions with equal area R1
area of original square is \({k^2}\) (A1)
so total shaded area is \(\frac{{{k^2}}}{4}\) (A1)
correct equation \(\frac{{{k^2}}}{4} = k\) A1
\({k^2} = 4k\) (A1)
valid attempt to solve their quadratic (M1)
eg \(k(k – 4),{\text{ }}k = 4{\text{ or }}k = 0\)
\(k = 4\) A1 N2
[7 marks]
Examiners report
[N/A]
[N/A]
[N/A]
