Question
(a) One atom of each of the four elements H, C, N and O can bond together in different ways.
Two examples are molecules of cyanic acid, HOCN, and isocyanic acid, HNCO. The atoms are bonded in the order they are written.
(i) Draw ‘dot-and-cross’ diagrams of these two acids, showing outer shell electrons only.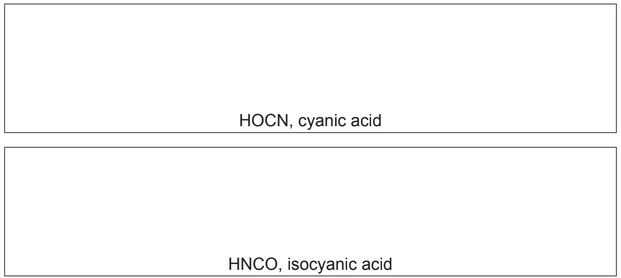
(ii) Suggest the values of the bond angles HNC and NCO in isocyanic acid.
HNC ………………………… NCO …………………………
(iii) Suggest which acid, cyanic or isocyanic, will have the shorter C–N bond length.
Explain your answer.
(b) (i) Isocyanic acid is a weak acid.
\(HNCO \leftrightarrow H^+ + NCO^–\) \(K_a = 1.2 × 10^{–4}\) mol\(dm^{–3}\)
Calculate the pH of a 0.10mol\(dm^{–3}\) solution of isocyanic acid.
pH = ………
(ii) Sodium cyanate, NaNCO, is used in the production of isocyanic acid.
Sodium cyanate is prepared commercially by reacting urea, \((NH_2)_2CO\), with sodium carbonate. Other products in this reaction are carbon dioxide, ammonia and steam.
Write an equation for the production of NaNCO by this method.
(c) Barium hydroxide, \(Ba(OH)_2\), is completely ionised in aqueous solutions.
During the addition of 30.0 \(cm^3\) of 0.100mol\(dm^{–3}\) \(Ba(OH)_2\) to 20.0\(cm^3\) of 0.100mol\(dm^{–3}\) isocyanic acid, the pH was measured.
(i) Calculate the \([OH^–]\) at the end of the addition.
\([OH^–]\) = ………………………… mol\(dm^{–3}\)
(ii) Use your value in (i) to calculate \([H^+]\) and the pH of the solution at the end of the addition.
final \([H^+]\) = ………………………… mol\(dm^{–3}\)
final pH = …………………………
(iii) On the following axes, sketch how the pH changes during the addition of a total of 30.0\(cm^3\) of 0.100mol\(dm^{–3}\) \(Ba(OH)_2\) to 20.0\(cm^3\) of 0.100mol\(dm^{–3}\) isocyanic acid.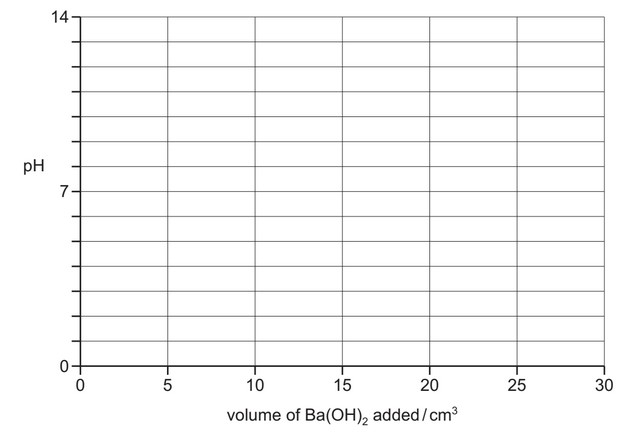
(d) The cyanate ion, \(NCO^–\), can act as a monodentate ligand.
(i) State what is meant by the terms
monodentate, ……………………………………………………………………………………………………….
ligand. …………………………………………………………………………………………………………………
Silver ions, \(Ag^+\), react with cyanate ions to form a linear complex.
(ii) Suggest the formula of this complex, including its charge.
(e) When heated with HCl(aq), organic isocyanates, RNCO, are hydrolysed to the amine salt,
\(RNH_3Cl\), and \(CO_2\).
\(RNCO + H_2O + HCl \rightarrow RNH_3Cl + CO_2\)
A 1.00g sample of an organic isocyanate, RNCO, was treated in this way, and the \(CO_2\) produced
was absorbed in an excess of aqueous \(Ba(OH)_2\) according to the equation shown. The solid
\(BaCO_3\) precipitated weighed 1.66g.
\(Ba(OH)_2(aq) + CO_2(g) \rightarrow BaCO_3(s) + H_2O(l)\)
(i) Calculate the number of moles of \(BaCO_3\) produced.
moles of \(BaCO_3\) = …………………………
(ii) Hence calculate the Mr of the organic isocyanate RNCO.
\(M_r\) of RNCO = …………………………
The R group in RNCO and \(RNH_3Cl\) contains carbon and hydrogen only.
(iii) Use your \(M_r\) value calculated in (ii) to suggest the molecular formula of the organic isocyanate RNCO.
molecular formula of RNCO ……………………………………………………………………………..
(iv) Suggest a possible structure of the amine \(RNH_2\), which forms the amine salt, \(RNH_3Cl\).
Answer/Explanation
Answer:
(a) (i) 
16 electrons on each diagram
(ii) HNC = 115–125° AND NCO = 180°
(iii) cyanic acid, because it’s a stronger / higher bond enthalpy / triple / C≡N / more electrons involved bond
(b) (i) \([H^+] = √([HNCO]K_a) = √(0.1 × 1.2 × 10^{–4})\) or 3.46 × \(10^{–3}\)
pH = log [\(H^+\)] = 2.5 (2.46)
(ii) \(Na_2CO_3 + 2(NH_2)_2CO → 2NaNCO + CO_2 + 2NH_3 + H_2O\)
(c) (i) \((n(OH^–)\) at start = (2 × 0.1 × 30) / 1000 = 6 × \(10^{–3}\) mol)
\((n(OH^–)\) reacted = (0.1 × 20) / 1000 = 2 × \(10^{–3}\) mol)
\(n(OH^–)\) remaining = (6–2) × \(10^{–3}\) = 4 × \(10^{–3}\) mol, (in 50 \(cm^3\))
so \([OH^–]_{end}\) = (4 × \(10^{–3}\) × 1000) / 50 = 0.08 mol \(dm^{–3}\)
(ii) \([H^+] = K_w / [OH^–] = (1 × 10^{–14}) / 0.08 = 1.25 × 10^{–13}\) mol \(dm^{–3}\)
so pH = –log(1.25 × \(10^{–13}\)) = 12.9
(iii) curve starts at 2.46 / 2.5
vertical portion (end point) at vol added = 10.0 \(cm^3\)
finishes at pH = 12.9
(d) (i) monodentate: (a species that) forms one dative / coordinate bond
ligand: a species that uses a lone pair of electrons to form a dative / coordinate bond to a metal atom / metal ion
(ii) \([Ag(NCO)_2]^–\) or \([Ag(OCN)_2]^–\) correct formula
correct charge
(e) (i) \(n(BaCO_3)\) =1.66 / 197.3 = 8.4(1) × \(10^{–3}\) mol
(ii) n(RNCO) = 8.41 × \(10^{–3}\) mol, so \(M_r\) = 1 / (8.41 × \(10^{–3}\)) = 119
(iii) molecular formula = \(C_7H_5NO\)
(iv) 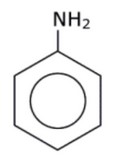
Question
Hydrogen halides are compounds formed when halogens (Group 17 elements) react with hydrogen.
The bond polarity of the hydrogen halides decreases from HF to HI.
Some relevant data are shown in the table
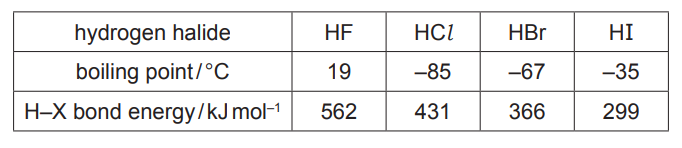
(a) (i) Explain the meaning of the term bond polarity [1]
(ii) Suggest why the boiling point of HF is much higher than the boiling points of the other hydrogen halides. [2]
(iii) Describe and explain the relative thermal stabilities of the hydrogen halides.
(b) The equation for the preparation of hydrogen chloride using concentrated sulfuric acid is shown.
$
\mathrm{H}_2 \mathrm{SO}_4+\mathrm{NaCl} \rightarrow \mathrm{NaHSO}_4+\mathrm{HCl}
$
(i) Use the Brønsted-Lowry theory of acids and bases to identify the base and its conjugate acid in this reaction. Explain your answer.
Brønsted-Lowry base $($ base-I) $=$
conjugate acid $($ acid-II) $=$[2]
(ii) Explain why the reaction of concentrated sulfuric acid and sodium iodide is not suitable for the preparation of hydrogen iodide.[2]
(c) Hydrogen chloride undergoes a reversible reaction with oxygen
$
4 \mathrm{HCl}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{Cl}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g})
$
The reaction is carried out at $400^{\circ} \mathrm{C}$ in the presence of a copper(II) chloride catalyst.
(i) Use the data in the table to calculate the overall enthalpy change of reaction.
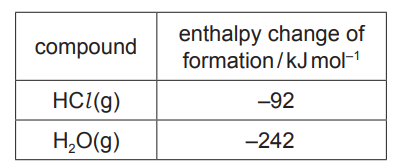
enthalpy change of reaction $=$
$\mathrm{kJmol}^{-1}[2]$
(ii) State the type of catalyst used in this reaction. Explain how a catalyst is able to increase the rate of a chemical reaction.[2]
(iii) The reaction exists in dynamic equilibrium.
The reaction was repeated at $1000^{\circ} \mathrm{C}$ and the same pressure.
State and explain the effect on the composition of the equilibrium mixture of the change in temperature. [2]
(iv) When $1.60 \mathrm{~mol}$ of $\mathrm{HCl}$ are mixed in a sealed container with $0.500 \mathrm{~mol}$ of $\mathrm{O}_2$ at $400^{\circ} \mathrm{C}$, $0.600 \mathrm{~mol}$ of $\mathrm{Cl}_2$ and $0.600 \mathrm{~mol}$ of $\mathrm{H}_2 \mathrm{O}$ are formed.
The total pressure inside the container is $1.50 \times 10^5 \mathrm{~Pa}$.
- Calculate the amounts, in mol, of $\mathrm{HCl}$ and $\mathrm{O}_2$ in the equilibrium mixture.
$
\begin{aligned}
& \mathrm{HCl}= \ldots \ldots . \ldots \mathrm{mol} \\
& \mathrm{O}_2=\ldots \ldots \mathrm{mol}
\end{aligned}
$
$\mathrm{mol}$
- Calculate the mole fraction of $\mathrm{Cl}_2$ and hence the partial pressure of $\mathrm{Cl}_2$ in the equilibrium mixture.
(v) In a separate experiment, an equilibrium reaction mixture was found to contain the four gases at the partial pressures shown in the table.

$
K_{\mathrm{p}}=\frac{\left(p_{\mathrm{Cl}}\right)^2 \times\left(p_{\mathrm{H}_2 \mathrm{O}}\right)^2}{\left(p_{\mathrm{HCl}}\right)^4 \times \mathrm{p}_{\mathrm{O}_2}}
$
Use this information and the expression given for $K_p$ to calculate a value for $K_p$. State the units of $K_{\mathrm{p}}$.
$
K_{\mathrm{p}}=
$
units $=$[2]
(vi) The reaction is repeated without a catalyst.
State the effect of this on $K_p$.[1] [Total: 22]
▶️Answer/Explanation
Ans:
(a)(i) bond in which the centres of positive and negative charges do not coincide
OR electron distribution is asymmetric /unequal
OR two (bonded) atoms are partially charged
(a)(ii) HF has the strongest (permanent) dipole–dipole/ van der Waals’
(forces)/HF has hydrogen bonding requires more energy to overcome (than weaker (permanent) dipole–dipole/van der Waals’ forces between other hydrogen halides)
(a)(iii) thermal stability of the hydrogen halides decreases down group (17) 1
larger (halogen) atoms /atomic radius (down group) / increased shielding 1
bond energies decrease / less energy required to break H–X
(b)(i)
M1 base is $\mathrm{Cl}^{-}$AND conjugate acid is $\mathrm{HCl}$ OR base is $\mathrm{HSO}_4^{-}$AND conjugate acid is $\mathrm{H}_2 \mathrm{SO}_4$
M2 $\mathrm{Cl}^{-} / \mathrm{HSO}_4^{-} /$base is a proton acceptor OR $\mathrm{HC} l / \mathrm{H}_2 \mathrm{SO}_4 /$ (conjugate) acid has one more $\mathrm{H}^{+}$
(b)(ii)
$\mathrm{H}_2 \mathrm{SO}_4$ is (too strong) an oxidising agent
$I_2$ would be formed instead
(c)(i) $\quad \Delta_{\mathrm{r}} \mathrm{H}=\Delta_{\mathrm{r}} \mathrm{H}$ \{products $\}-\Delta_{\mathrm{r}} \mathrm{H}\{$ reactants $\}=2 \times(-242)-4 \times(-92)$
= –116 (sign AND answer)
(c)(ii) heterogeneous (catalyst) 1
provides an alternative reaction pathway of lower activation energy 1
(c)(iii) reaction is exothermic
(increased temperature) shifts equilibrium to the left AND decreases yield of products $\left(\mathrm{Cl}_2\right.$ and /or $\left.\mathrm{H}_2 \mathrm{O}\right) /$ less product formed
(c)(iv)
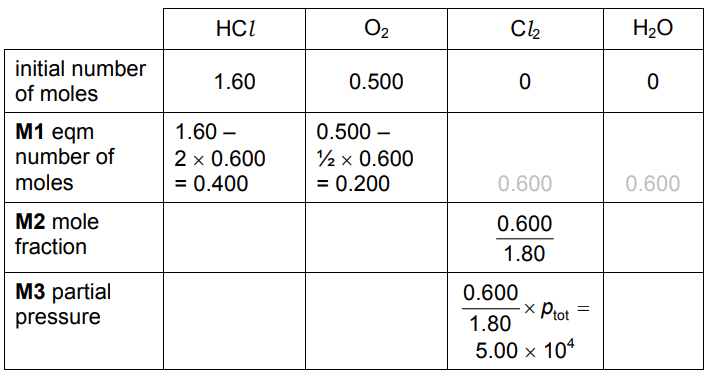
(c)(v) $K_p=\frac{\left(3.6 \times 10^4\right)^2 \times\left(3.6 \times 10^4\right)^2}{\left(4.8 \times 10^4\right)^4 \times 3.0 \times 10^4}=1.05 \times 10^{-5}$
units $=\mathrm{Pa}^{-1}$
2(c)(vi) $\quad K_p$ would not change