Question
(a) The lattice energies of three ionic compounds are given.
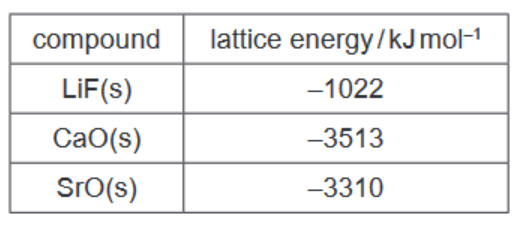
(i) Define the term lattice energy[2]
(ii) Explain why the lattice energy of $\mathrm{CaO}$ is more exothermic than the lattice energy of LiF.[1]
(iii) Use the data in the table to estimate approximate values for the lattice energies of magnesium oxide and barium oxide.
$\Delta H_{\text {latt }} \mathrm{MgO}(\mathrm{s})=\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . . . \mathrm{kJ} \mathrm{mol}^{-1}$
$\Delta H_{\mathrm{latt}} \mathrm{BaO}(\mathrm{s})=\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . . \mathrm{kJ} \mathrm{mol}^{-1}$
(b) (i) Write an equation for the reaction between $\mathrm{BaO}$ and $\mathrm{H}_2 \mathrm{O}$. Include state symbols. [1]
(ii) State and explain how the solubilities of the hydroxides of the Group 2 elements vary down the group.
(c) Use the following data and relevant data from the Data Booklet to calculate a value for the lattice energy of magnesium fluoride, $\mathrm{MgF}_2(\mathrm{~s})$.
You might find it helpful to construct an energy cycle.
Show your working.
electron affinity of $F(\mathrm{~g}) \quad=-348 \mathrm{~kJ} \mathrm{~mol}^{-1}$
enthalpy change of atomisation of $\mathrm{Mg}(\mathrm{s})=+147 \mathrm{~kJ} \mathrm{~mol}^{-1}$
enthalpy change of formation of $\mathrm{MgF}_2(\mathrm{~s})=-1102 \mathrm{~kJ} \mathrm{~mol}^{-1}$
$
\Delta H_{\text {latt }} \mathrm{MgF}_2(\mathrm{~s})=
$
(d) (i) Define the term electron affinity.
(ii) The electron affinity of carbon, $\mathrm{C}(\mathrm{g})$, is $-120 \mathrm{~kJ} \mathrm{~mol}^{-1}$.
Suggest an explanation for the difference between the electron affinity of fluorine and the electron affinity of carbon. [1] [Total: 15]
▶️Answer/Explanation
Ans:
2(a)(i) M1 energy released when 1 mole of an ionic compound is formed [1]
M2 from gaseous ions (under standard conditions) [1]
(a)(ii) $\mathrm{Ca}^{2+} \& \mathrm{O}^{2-}$ have a higher charge / charge density (than $\mathrm{Li}^{+}$and $\mathrm{F}^{-}$) [1]
2(a)(iii) MgO -3600 or more negative AND BaO -3200 or less negative BOTH [1]
2(b)(ii) M1 (solubility) increases (down the group) [1]
M2 both $\Delta H_{\text {latt }}$ and $\Delta H_{\text {hyd }}$ become less exothermic / less negative [1]
M3 $\Delta H_{\text {latt }}$ changes more / is dominant factor [1]
M4 $\Delta H_{\text {sol }}$ becomes more negative / more exothermic [1]
‘2(c) M1: Use of $2 \times-348$ (EAF) and +158 (bond energy of $F_2$ ) [1]
M2: Use of +147 (at Mg) and +736 and +1450 (IEs of Mg) [1]
M3: evaluation and calculation of their answer $(-1102-(147+158+736+1450-696))=-2897\left(\mathrm{~kJ} \mathrm{~mol}^{-1}\right)[1]$ ecf
2(d)(i) $\quad$ (energy change) when an / one electron is added to
- each atom / ion in one mole of
- gaseous atoms/ions
mark as $\bullet \checkmark \checkmark[2]$
2(d)(ii) $F$ has greater nuclear charge / more protons
AND greater attraction between $F$ atom / nucleus and the electrons
- $\checkmark$ BOTH [1]
Question
(a) The solubility of the Group 2 sulfates decreases down the group.
Explain this trend.
(b) Describe what is observed when magnesium and barium are reacted separately with an excess of dilute sulfuric acid.
magnesium ………………………………………………………………………………………………………………..
barium ……………………………………………………………………………………………………………………….
(c) The solubility product, \(K_{sp}\), of \(BaSO_4\) is \(1.08 × 10^{–10}mol^2dm^{–6}\) at 298K.
Calculate the solubility of \(BaSO_4\) in g per \(100cm^3\) of solution.
solubility of BaSO$_4$ = ………………………… g per \(100cm^3\) of solution
(d) (i) The equation for the formation of a gaseous sulfate ion is shown.
\(S(s) + 2O_2(g) + 2e^–→ SO_4^{2–}(g)\) \(∆H = ∆H_f^{\theta}\) of \(SO_4^{2–}(g)\)
Calculate the standard enthalpy change of formation, \(\∆H_f^{\theta}\), of \(SO_4^{2-}(g)\). It may be helpful to draw a labelled energy cycle. Use relevant data from Table 1.1 in your calculations.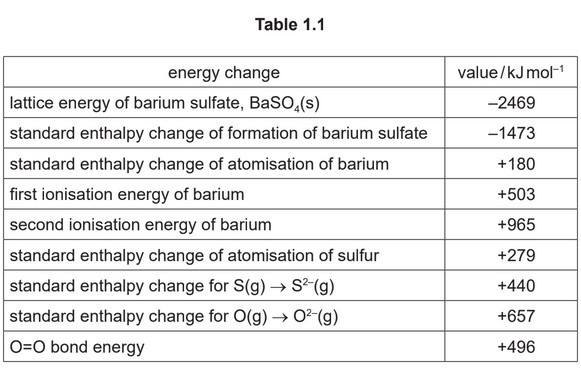
\(∆H_r^{\theta}\) of \(SO_4^{2-}(g)\) = ………………… kJ \(mol^{-1}\)
(ii) Suggest how the lattice energy of \(BaSO_4(s)\) differs from the lattice energy of \(Cs_2SO_4(s)\).
Explain your answer.
(e) The reaction of solid hydrated barium hydroxide, \(Ba(OH)_2•8H_2O\), with ammonium salts is endothermic.
(i) Calculate the minimum temperature at which the reaction of \(Ba(OH)_2•8H_2O with NH_4NO_3\) becomes feasible. Show all your working.
\(Ba(OH)_2•8H_2O(s) + 2NH_4NO_3(s) → 2NH_3(g) + Ba(NO_3)_2(s) + 10H_2O(l)\) \(∆H_r^{\theta} = +132 kJ mol^{-1}\)
\(∆S^{\theta} = +616 JK^{-1}mol^{-1}\)
temperature = ………………. \(^o C\)
(ii) Barium hydroxide reacts readily with ammonium chloride on mixing at room temperature.
\(Ba(OH)_2•8H_2O(s) + 2NH_4Cl(s) → 2NH_3(g) + BaCl_2•2H_2O(s) + 8H_2O(l)\) \(∆H_r^{\theta}\)= +133kJ\(mol^{–1}\)
Some relevant standard entropies are given in Table 1.2.
Calculate the standard Gibbs free energy change, \(∆G^o\) , for this reaction at 25°C.
\(∆G^o = ………………………… kJmol^{–1}\)
Answer/Explanation
Answer:
(a) M1 \(\∆H_{latt}\) and \(∆H_{hyd}\) decrease / both become less exothermic / less negative
M2 \(∆H_{latt}\) decreases / changes less/becomes less exothermic by a smaller extent OR \(∆H_{hyd}\) decreases / changes more / dominant factor
M3 \(∆H_{sol}\) becomes less exothermic / less negative
OR \(∆H_{sol}\) becomes (more) endothermic / (more) positive
OR \(∆H_{sol}\) = \(∆H_{hyd} – ∆H_{latt}\) expression AND reaction becomes less exothermic
(b) Mg: fizzing
Ba: (fizzing and) white solid/ppt forms
(c) M1 solubility of \(BaSO_4 = √1.08 \times 10^{–10} = 1.04 \times 10^{–5} (mol dm^{–3})\)
M2 = \(1.04 \times 10^{–5} \times 233.4 / 10 = 2.43 times 10^{–4}\) (g per 100 \(cm^3\) of solution) min 2sf
(d) (i) \(–1473 = 180 + 503 + 965 + ∆H_f^{\theta}\) – 2469
\(∆H_f^{\theta}\) of \(SO_4^{2-}(g)\) = – 625 kJ \(mol^{-1}\)
M1 correct five values used [1]
M2 only correct five values used [1]
M3 correct signs and evaluation [1]
(ii) \(BaSO_4\) is more negative/bigger
as \(Ba^{2+}\) is smaller OR \(Ba^{2+}\) has a larger charge
stronger force of attraction between the ions
One mark for two correct
Two marks for all three correct
(e) (i) M1 \(∆G^o = 0\) so \(T = ∆H_r^o / ∆S^o\)
M2
T = 132 / 0.616 = 214.3 K
T = –58.7 °C min 2sf
(ii) M1 \(∆S^0 = (203 + (70 \times 8) + (2 times 192)) – (427 – (2 \times 95)) = +530 J K^{–1} mol^{–1}\)
M2 \(∆G^o = ∆H^o – T∆S^o\)
M3 \(∆G^o = 133 – (298 \times 0.530) = –24.9 kJ mol^{–1}\) ecf 1dp min