Question
One method of producing hydrogen from natural gas is the reaction between hydrogen sulfide and methane.
$
2 \mathrm{H}_2 \mathrm{~S}(\mathrm{~g})+\mathrm{CH}_4(\mathrm{~g}) \rightleftharpoons \mathrm{CS}_2(\mathrm{~g})+4 \mathrm{H}_2(\mathrm{~g})
$
(a) Write the expression for $K_p$ for this reaction, and state its units.
$
K_{\mathrm{p}}=
$
units[2]
(b) The initial partial pressures of the two gases in a mixture at $1000 \mathrm{~K}$ are recorded.
$
\mathrm{H}_2 \mathrm{~S}(\mathrm{~g}) 200 \mathrm{~atm} \quad \mathrm{CH}_4(\mathrm{~g}) \quad 100 \mathrm{~atm}
$
The mixture is left to reach equilibrium.
It is found that the equilibrium partial pressure of $\mathrm{CS}_2(\mathrm{~g})$ is $2 \mathrm{~atm}$ and that of the remaining $\mathrm{CH}_4(\mathrm{~g})$ is $98 \mathrm{~atm}$.
(i) Calculate the equilibrium partial pressures of $\mathrm{H}_2 \mathrm{~S}(\mathrm{~g})$ and $\mathrm{H}_2(\mathrm{~g})$.
$p\left(\mathrm{H}_2 \mathrm{~S}\right)=$ atm
$p\left(\mathrm{H}_2\right)=$ atm [2]
(ii) Calculate the value of $K_{\mathrm{p}}$ at this temperature.
$
K_p=
$
(c) (i) Predict the sign of $\Delta S^{\ominus}$ for this reaction. Explain your answer.
$
2 \mathrm{H}_2 \mathrm{~S}(\mathrm{~g})+\mathrm{CH}_4(\mathrm{~g}) \rightleftharpoons \mathrm{CS}_2(\mathrm{~g})+4 \mathrm{H}_2(\mathrm{~g}) \quad \Delta H^{\ominus}=+241 \mathrm{kJmol}^{-1}
$ [1]
The free energy change, $\Delta G^{\ominus}$, for this reaction at $1000 \mathrm{~K}$ is $+51 \mathrm{~kJ} \mathrm{~mol}^{-1}$.
(ii) Calculate the value of $\Delta S^\theta$ for this reaction, stating its units.
$\Delta S^\theta=$ units [2]
(d) How would the value of $\Delta G^{\ominus}$, and hence the spontaneity (feasibility) of this reaction change as the temperature increases? Explain your answer. [2] [Total: 10]
▶️Answer/Explanation
Ans:
(a) $\quad K_{\mathrm{p}}=\left\{\mathrm{p}\left(\mathrm{CS}_2\right) \times\left(\mathrm{p}\left(\mathrm{H}_2\right)\right)^4\right\} /\left\{\left(\mathrm{p}\left(\mathrm{H}_2 \mathrm{~S}\right)\right)^2 \times \mathrm{p}\left(\mathrm{CH}_4\right)\right\}$ units: $\mathrm{atm}^2$ OR Pa
(b) (i) $\quad \begin{aligned} & \mathrm{p}\left(\mathrm{H}_2 \mathrm{~S}\right)=196 \mathrm{~atm} \\ & \mathrm{p}\left(\mathrm{H}_2\right)=8 \mathrm{~atm}\end{aligned}$
(ii) $\quad K_p=\left(2 \times 8^4\right) /\left(196^2 \times 98\right)=2.176 \times 10^{-3}$
(c) (i) $\Delta S^{\circ}$ will be positive, because more gas moles on the RHS/products
(ii) $\quad \Delta S^{\circ}=\left(\Delta H^{\circ}-\Delta G^{\circ}\right) / T=(241-51) / 1000=0.19$ OR 190
(d) $\quad \Delta G^{\ominus}$ will become less positive/more negative as $T$ increases, …because $\Delta S^0$ is positive (or $-T \Delta S^0$ is more negative) therefore the reaction becomes more feasible/spontaneous as $T$ increases
Question
(a) The solubility of the Group 2 sulfates decreases down the group.
Explain this trend.
(b) Describe what is observed when magnesium and barium are reacted separately with an excess of dilute sulfuric acid.
magnesium ………………………………………………………………………………………………………………..
barium ……………………………………………………………………………………………………………………….
(c) The solubility product, \(K_{sp}\), of \(BaSO_4\) is \(1.08 × 10^{–10}mol^2dm^{–6}\) at 298K.
Calculate the solubility of \(BaSO_4\) in g per \(100cm^3\) of solution.
solubility = ………………………… g per \(100cm^3\) of solution
(d) (i) The equation for the formation of a gaseous sulfate ion is shown.
\(S(s) + 2O_2(g) + 2e^–→ SO_4^{2–}(g)\) \(∆H = ∆H_f^{\theta}\) of \(SO_4^{2–}(g)\)
Calculate the standard enthalpy change of formation, \(\∆H_f^{\theta}\), of \(SO_4^{2-}(g)\). It may be helpful to draw a labelled energy cycle. Use relevant data from Table 1.1 in your calculations.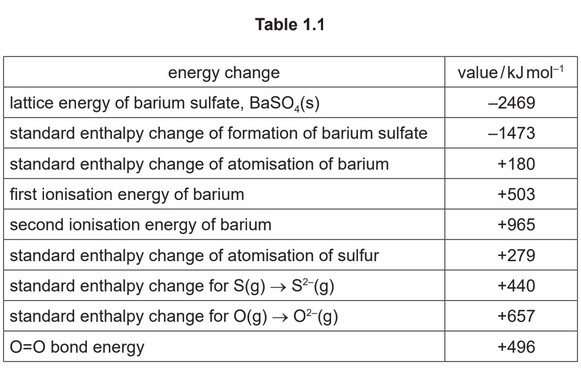
\(∆H_r^{\theta}\) of \(SO_4^{2-}(g)\) = ………………… kJ \(mol^{-1}\)
(ii) Suggest how the lattice energy of \(BaSO_4(s)\) differs from the lattice energy of \(Cs_2SO_4(s)\).
Explain your answer.
(e) The reaction of solid hydrated barium hydroxide, \(Ba(OH)_2•8H_2O\), with ammonium salts is endothermic.
(i) Calculate the minimum temperature at which the reaction of \(Ba(OH)_2•8H_2O with NH_4NO_3\) becomes feasible. Show all your working.
\(Ba(OH)_2•8H_2O(s) + 2NH_4NO_3(s) → 2NH_3(g) + Ba(NO_3)_2(s) + 10H_2O(l)\) \(∆H_r^{\theta} = +132 kJ mol^{-1}\)
\(∆S^{\theta} = +616 JK^{-1}mol^{-1}\)
temperature = ………………. \(^o C\)
(ii) Barium hydroxide reacts readily with ammonium chloride on mixing at room temperature.
\(Ba(OH)_2•8H_2O(s) + 2NH_4Cl(s) → 2NH_3(g) + BaCl_2•2H_2O(s) + 8H_2O(l)\) \(∆H_r^{\theta}\)= +133kJ\(mol^{–1}\)
Some relevant standard entropies are given in Table 1.2.
Calculate the standard Gibbs free energy change, \(∆G^o\) , for this reaction at 25°C.
\(∆G^o = ………………………… kJmol^{–1}\)
Answer/Explanation
Answer:
(a) M1 \(\∆H_{latt}\) and \(∆H_{hyd}\) decrease / both become less exothermic / less negative
M2 \(∆H_{latt}\) decreases / changes less/becomes less exothermic by a smaller extent OR \(∆H_{hyd}\) decreases / changes more / dominant factor
M3 \(∆H_{sol}\) becomes less exothermic / less negative
OR \(∆H_{sol}\) becomes (more) endothermic / (more) positive
OR \(∆H_{sol}\) = \(∆H_{hyd} – ∆H_{latt}\) expression AND reaction becomes less exothermic
(b) Mg: fizzing
Ba: (fizzing and) white solid/ppt forms
(c) M1 solubility of \(BaSO_4 = √1.08 \times 10^{–10} = 1.04 \times 10^{–5} (mol dm^{–3})\)
M2 = \(1.04 \times 10^{–5} \times 233.4 / 10 = 2.43 times 10^{–4}\) (g per 100 \(cm^3\) of solution) min 2sf
(d) (i) \(–1473 = 180 + 503 + 965 + ∆H_f^{\theta}\) – 2469
\(∆H_f^{\theta}\) of \(SO_4^{2-}(g)\) = – 625 kJ \(mol^{-1}\)
M1 correct five values used [1]
M2 only correct five values used [1]
M3 correct signs and evaluation [1]
(ii) \(BaSO_4\) is more negative/bigger
as \(Ba^{2+}\) is smaller OR \(Ba^{2+}\) has a larger charge
stronger force of attraction between the ions
One mark for two correct
Two marks for all three correct
(e) (i) M1 \(∆G^o = 0\) so \(T = ∆H_r^o / ∆S^o\)
M2
T = 132 / 0.616 = 214.3 K
T = –58.7 °C min 2sf
(ii) M1 \(∆S^0 = (203 + (70 \times 8) + (2 times 192)) – (427 – (2 \times 95)) = +530 J K^{–1} mol^{–1}\)
M2 \(∆G^o = ∆H^o – T∆S^o\)
M3 \(∆G^o = 133 – (298 \times 0.530) = –24.9 kJ mol^{–1}\) ecf 1dp min