Question
A solution is made by dissolving $\mathrm{CuSO}_4 \cdot 5 \mathrm{H}_2 \mathrm{O}$ in an excess of aqueous ammonia. This solution contains the copper complex $\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2^{2+}}$.
(a) (i) Write an expression for the $K_{\text {stab }}$ of $\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}$.
$
K_{\mathrm{stab}}=
$[1]
(ii) State the colour of the solution of $\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}$. [1]
The solution of $\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}$ is heated gently in a fume cupboard so that $\mathrm{NH}_3$ is released. Some $\mathrm{NH}_3$ remains in solution and some forms $\mathrm{NH}_3$ gas. The colour of the solution changes; a precipitate of $\mathrm{Cu}(\mathrm{OH})_2$ forms and is collected.
A sample of $\mathrm{Cu}(\mathrm{OH})_2$ is added to concentrated hydrochloric acid. A reaction takes place forming a coloured copper complex, Y.
A sample of $\mathrm{Cu}(\mathrm{OH})_2$ is added to dilute sulfuric acid. A reaction takes place forming a coloured copper complex, $\mathbf{Z}$.
$\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}, \mathbf{Y}$ and $\mathbf{Z}$ are different colours.
(b) Suggest an equation for the reaction of $\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}$ to form $\mathrm{Cu}(\mathrm{OH})_2$ as the aqueous solution of $\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}$ is heated.[1]
(c) Suggest an equation for the reaction of $\mathrm{Cu}(\mathrm{OH})_2$ with concentrated hydrochloric acid, forming $\mathbf{Y}$. [5]
(d) Complete the table with the colour and geometry of complex $\mathbf{Y}$ and the colour, geometry and formula of complex $\mathbf{Z}$.

e) Explain why complexes Y and Z are coloured and why their colours are different. [5][Total: 12]
▶️Answer/Explanation
Ans:
5(a)(i) $\quad K$ stab $=\left[\left(\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right)^{2+}\right] /\left[\left(\mathrm{Cu}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right)^{2+}\right]\left[\mathrm{NH}_3\right]^4[1]$
5(a)(ii) deep / dark / royal blue [1]
$
\begin{array}{ll}
\text { 5(b) } & {\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}+2 \mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{Cu}(\mathrm{OH})_2+2 \mathrm{NH}_4+2 \mathrm{NH}_3[1]} \\
& \mathrm{OR}\left[\mathrm{Cu}\left(\mathrm{NH}_3\right)_4\right]^{2+}+2 \mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{Cu}(\mathrm{OH})_2+2 \mathrm{H}^{+}+4 \mathrm{NH}_3 \\
\text { 5(c) } & \left.\mathrm{Cu}(\mathrm{OH})_2+4 \mathrm{HCl} \rightarrow[\mathrm{CuCl})_4\right]^{2-}+2 \mathrm{H}_2 \mathrm{O}+2 \mathrm{H}^{+} \\
& \mathrm{OR} \mathrm{Cu}(\mathrm{OH})_2+4 \mathrm{Cl}^{-}+2 \mathrm{H}^{+} \rightarrow\left[\mathrm{CuCl} l_4\right]^{2-}+2 \mathrm{H}_2 \mathrm{O}
\end{array}
$
5(c) $\mathrm{Cu}(\mathrm{OH})_2+4 \mathrm{HCl} \rightarrow\left[\mathrm{CuCl}_4\right]^{2-}+2 \mathrm{H}_2 \mathrm{O}+2 \mathrm{H}^{+}$
OR Cu $(\mathrm{OH})_2+4 \mathrm{Cl}^{-}+2 \mathrm{H}^{+} \rightarrow\left[\mathrm{CuCl}_4\right]^{2-}+2 \mathrm{H}_2 \mathrm{O}$
[CuCl4 $]^{2-}$ complex including charge [1] rest of equation fully correct [1]
(d)
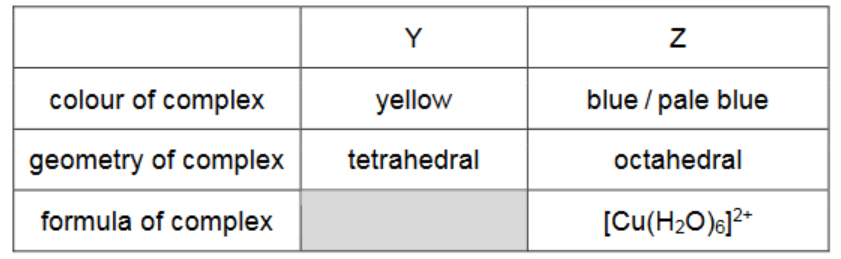
one mark for any three cells [1]
two marks for all five cells [2]
2
5(e) M1: d orbitals splits into two sets of energy levels of different energy [1]
M2: wavelength / frequency / light / photon / hν absorbed [1]
M3: electron(s) promoted / excited [1]
M4: colour seen is complementary (to colour absorbed) [1]
M5: d–d energy gap / ΔE is different for Y and Z
AND so different frequency / wavelength of light absorbed [1]
Question
(a) Silver carbonate, $\mathrm{Ag}_2 \mathrm{CO}_3$, is sparingly soluble in water. The numerical value of the solubility product, $K_{\mathrm{sp}}$, for silver carbonate is $6.3 \times 10^{-12}$ at $25^{\circ} \mathrm{C}$.
(i) Write an expression for the solubility product, $\mathrm{K}_{\mathrm{sp}}$, of $\mathrm{Ag}_2 \mathrm{CO}_3$, and state its units.
$
K_{\mathrm{sp}}=
$ units = ………………………… [2]
(ii) Calculate the equilibrium concentration of $\mathrm{Ag}^{+}$in a saturated solution of $\mathrm{Ag}_2 \mathrm{CO}_3$ at $25^{\circ} \mathrm{C}$.
$\left[\mathrm{Ag}^{+}\right]=$ $\mathrm{moldm}^{-3}$ [1]
$\left[\mathrm{Ag}^{+}\right]=$ $\mathrm{moldm}^{-3}$ [1]
(iii) Solid $\mathrm{Ag}_2 \mathrm{CO}_3$ is stirred at $25^{\circ} \mathrm{C}$ with $0.050 \mathrm{moldm}^{-3} \mathrm{AgNO}_3$ until no more $\mathrm{Ag}_2 \mathrm{CO}_3$ dissolves. Calculate the concentration of carbonate ions, $\left[\mathrm{CO}_3{ }^{2-}\right]$, in this solution.
$
\left[\mathrm{CO}_3{ }^{2-}\right]=
$
$\mathrm{moldm}^{-3}$ [1]
(iv) An electrochemical cell is set up to measure the electrode potential, $E$, for the $\mathrm{Ag}^{+} / \mathrm{Ag}$ half-cell using the saturated $\mathrm{Ag}_2 \mathrm{CO}_3(\mathrm{aq})$ with a standard hydrogen electrode.
Use the Data Booklet, your answer to (a)(ii), and the Nernst equation to calculate the electrode potential, $E$, for this $\mathrm{Ag}^{+} / \mathrm{Ag}$ half-cell.
$E$ for $\mathrm{Ag}^{+} / \mathrm{Ag}$ half-cell $=$ $\mathrm{V}[\mathrm{s}]$
(b) Silver chloride, $\mathrm{AgCl}$, is sparingly soluble in water. The equation for the enthalpy change of solution is shown.
$
\operatorname{AgCl}(\mathrm{s}) \rightarrow \mathrm{Ag}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq}) \quad \Delta H_{\text {sol }}^{\ominus}=+65.5 \mathrm{~kJ} \mathrm{~mol}^{-1}
$
Standard entropies are shown in the table.

(i) Calculate the standard entropy change of solution, $\Delta S^\theta$.
$\Delta S^{\ominus}=\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . \mathrm{JK}^{-1} \mathrm{~mol}^{-1}[1]$
(ii) Explain, with the aid of a calculation, why $\mathrm{AgCl}$ is insoluble in water at $25^{\circ} \mathrm{C}$.
You should use data from this question and your answer to (b)(i).
(ii) Explain, with the aid of a calculation, why $\mathrm{AgC} l$ is insoluble in water at $25^{\circ} \mathrm{C}$. You should use data from this question and your answer to (b)(i). [3] [Total: 10]
▶️Answer/Explanation
Ans:
(a)(i) $\begin{aligned} & \text { M1 } K_{\mathrm{sp}}=\left[\mathrm{Ag}^{+}\right]^2\left[\mathrm{CO}_3^{2-}\right] \\ & \text { M2 units }=\mathrm{mol}^3 \mathrm{dm}^{-9}\end{aligned}$
7(a)(ii) $\begin{aligned} & x=\sqrt[3]{6} .3 \times 10^{-12} / 4=1.16 \times 10^{-4}\left(\mathrm{~mol} \mathrm{dm}^{-3}\right) \\ & {\left[\mathrm{Ag}^{+}\right]=1.16 \times 10^{-4} \times 2=2.33 \times 10^{-4}\left(\mathrm{~mol} \mathrm{dm^{-3 }}\right) \min 2 \mathrm{sf}} \\ & \end{aligned}$
(a)(iii) $
6.3 \times 10^{-12}=[0.05]^2\left[\mathrm{CO}_3{ }^{2-}\right]
$
$\left[\mathrm{CO}_3{ }^{2-}\right]=2.52 \times 10^{-9}\left(\mathrm{~mol} \mathrm{dm}^{-3}\right) \min 2 \mathrm{sf}$
a)(iv) M1 $E=E^0+0.059 \log \left[\mathrm{Ag}^{+}\right]$
M2 $E=0.80+0.059 \log \left(1.2 \times 10^{-4}\right)=0.57 \mathrm{~V}$ ecf from (a)(ii) $\min 2 \mathrm{sf}$
b)(i) $\Delta S^{\circ}=72.7+56.5-96.2=+33.0 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$
(b)(ii) M1 $\Delta G=\Delta H^{\ominus}-\mathrm{T} \Delta S^{\ominus}$
M2 $\Delta G=(65.5)-(298 \times 0.033)=+55.7 \mathrm{~kJ}^{-1} \mathrm{~mol}^{-1} \min 3 s f$
M3 $\Delta G=$ positive so not feasible/spontaneous