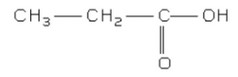Question [(a) (i) ]2023-May-Chemistry_paper_2__TZ2_HL
Topic: Stoichiometric relationships
Given: Analytical and spectroscopic methodologies empower chemists in discerning and elucidating compound structures. A mysterious organic compound, denoted as X, exclusively composed of carbon, hydrogen, and oxygen, was discovered to consist of 48.6% carbon and 43.2% oxygen.
Calculate: Ascertain the empirical formula.
▶️Answer/Explanation
Ans:
To determine the empirical formula of the unknown organic compound \(X\), we need to find the simplest whole number ratio of atoms of each element in the compound.
Given:
Percentage of carbon (C) in compound \(X\) = 48.6%
Percentage of oxygen (O) in compound \(X\) = 43.2%
To find the percentage of hydrogen (H) in compound \(X\), we can use the fact that the percentages of all elements in a compound must add up to 100%. Therefore, the percentage of hydrogen can be calculated as follows:
\[ \text{Percentage of hydrogen} = 100\% – (\text{Percentage of carbon} + \text{Percentage of oxygen}) \]
\[ \text{Percentage of hydrogen} = 100\% – (48.6\% + 43.2\%) \]
\[ \text{Percentage of hydrogen} = 8.2\% \]
Now, we can convert these percentages to masses (assume a total mass of 100 g for ease of calculation):
Mass of carbon (C) = \(48.6\% \times 100 \, \text{g} = 48.6 \, \text{g}\)
Mass of hydrogen (H) = \(8.2\% \times 100 \, \text{g} = 8.2 \, \text{g}\)
Mass of oxygen (O) = \(43.2\% \times 100 \, \text{g} = 43.2 \, \text{g}\)
Next, we need to determine the moles of each element in the compound using their respective molar masses:
Molar mass of carbon (C) = \(12.01 \, \text{g/mol}\)
Molar mass of hydrogen (H) = \(1.008 \, \text{g/mol}\)
Molar mass of oxygen (O) = \(16.00 \, \text{g/mol}\)
Now, we can calculate the moles of each element:
Moles of carbon (C) = \(\frac{48.6 \, \text{g}}{12.01 \, \text{g/mol}} \approx 4.05 \, \text{mol}\)
Moles of hydrogen (H) = \(\frac{8.2 \, \text{g}}{1.008 \, \text{g/mol}} \approx 8.13 \, \text{mol}\)
Moles of oxygen (O) = \(\frac{43.2 \, \text{g}}{16.00 \, \text{g/mol}} \approx 2.70 \, \text{mol}\)
Now, we find the simplest whole number ratio of moles of each element by dividing each by the smallest number of moles (which is approximately 2.70 mol for oxygen):
Ratio of moles of carbon (C) = \(\frac{4.05 \, \text{mol}}{2.70 \, \text{mol}} \approx 1.50\)
Ratio of moles of hydrogen (H) = \(\frac{8.13 \, \text{mol}}{2.70 \, \text{mol}} \approx 3.01\)
Ratio of moles of oxygen (O) = \(\frac{2.70 \, \text{mol}}{2.70 \, \text{mol}} = 1.00\)
These ratios represent the subscripts of each element in the empirical formula. To obtain whole numbers, we can multiply each ratio by a common factor. In this case, the smallest ratio is 1.00 for oxygen, so we can multiply each ratio by 2 to obtain whole numbers:
Ratio of carbon (C) = 1.50 × 2 ≈ 3
Ratio of hydrogen (H) = 3.01 × 2 ≈ 6
Ratio of oxygen (O) = 1.00 × 2 = 2
Therefore, the empirical formula of the unknown organic compound \(X\) is \(C_3H_6O_2\).
Question [(a) (ii) ]2023-May-Chemistry_paper_2__TZ2_HL
Topic:Periodic table
Given:
Discuss: Utilizing section 28 of the data booklet, determine the fragments accountable for the peaks observed at m/z 74 and 45.
m/z 74:
m/z 45:
▶️Answer/Explanation
Ans:
m/z 74: molecular ion / \(M^+\) / \(C_3H_6O_2^+\)
m/z 45: \(COOH^+ / C_2H_5O^+\)
Question [(a) (iii) ]2023-May-Chemistry_paper_2__TZ2_HL
Topic:Bonding Properties
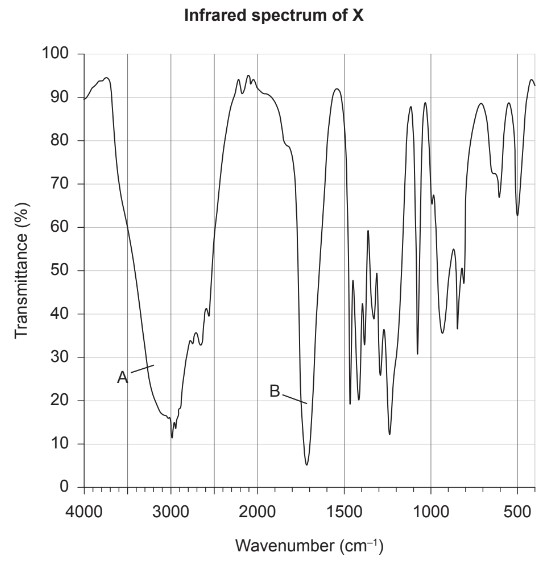
Discuss: Identify the primary bonds contributing to peaks A and B with reference to section 26 of the data booklet.
A:
B:
▶️Answer/Explanation
Ans:
A: O-H in carboxylic acids
B: C=O
Question [(a) (iv) ]2023-May-Chemistry_paper_2__TZ2_HL
Topic:Stuctural Formula
Discuss: The structural formula of X.
▶️Answer/Explanation
Ans: