Question
Which statement about scalar and vector quantities is correct?
A A scalar quantity has direction but not magnitude.
B A scalar quantity has magnitude but not direction.
C A vector quantity has direction but not magnitude.
D A vector quantity has magnitude but not direction.
Answer/Explanation
Ans: B
A scalar quantity has magnitude and no direction.
A vector quantity has both magnitude and direction.
Question
An aircraft heads in a direction at an angle θ east of north with a horizontal velocity relative to the air of 800 km h–1. The wind blows with a horizontal velocity of 200 km h–1 from east to west, as shown.
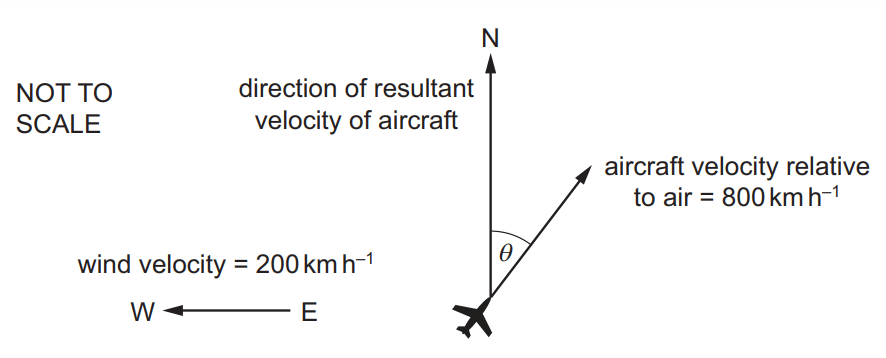
The resultant velocity of the aircraft is in a direction due north.
What is angle θ and what is the magnitude of the resultant velocity?
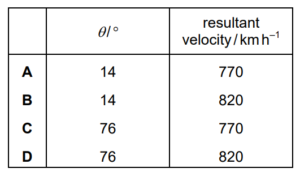
Answer/Explanation
Ans:A
We can see that the velocity of the aircraft relative to the air has two components: a vertical component pointing north and a horizontal component pointing east. We can use trigonometry to find the magnitudes of these components:
Vertical component = 800 km/h * sin(90-θ)
Horizontal component = 800 km/h * cos(90-θ)
The wind is blowing from east to west, so it is perpendicular to the direction of the aircraft. Therefore, it will not affect the vertical component of the aircraft’s velocity, but it will affect the horizontal component. The resulting horizontal component will be:
Horizontal component = 800 km/h * cos(90-θ) – 200 km/h
Now, we can use the fact that the resultant velocity is due north to find the angle θ. Since the vertical component of the aircraft’s velocity is pointing north, and the wind is not affecting it, the vertical component of the resultant velocity must also be pointing north. Therefore:
800 km/h * sin(90-θ) = Resultant velocity
We also know that the horizontal component of the resultant velocity is zero, since it is due north. Therefore:
800 km/h * cos(90-θ) – 200 km/h = 0
Now, we can solve for cos(θ):
cos(90-θ) = 200 km/h / 800 km/h = 0.25
θ = 90 – cos^(-1)(0.25) = 14 degrees
Finally, we can find the magnitude of the resultant velocity:
Resultant velocity = 800 km/h * sin(θ) = 770 km/h
Therefore, the angle θ is 14 degrees and the magnitude of the resultant velocity is approximately 770 km/h.
Question
A force of 10 N and a force of 5 N act on an object. 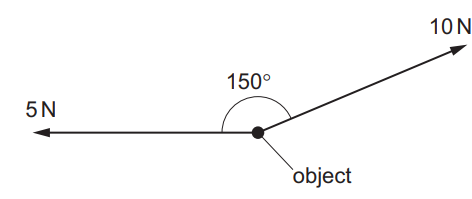
The angle between the forces is 150º. The resultant force on the object can be resolved into a pair of perpendicular components.
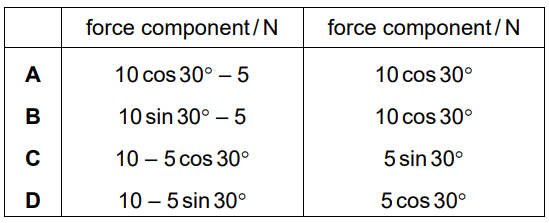
Which row shows numerical expressions for a possible pair of perpendicular components?
Answer/Explanation
Ans:C
If we consider x axis along the 10 N force, then the component of the resultant force in the x direction is given as,
F_x = (10 – 5cos (180-150) )
=10 – 5 cos 30
The y component will be given as,
F_y = 5 sin 30
Hence the option (C) is correct.
Question
A velocity vector is shown.
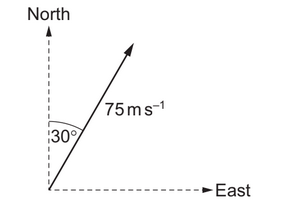
What are the components of the velocity vector in the northerly and in the easterly directions?

Answer/Explanation
Ans:
C
The component of the velocity in the easterly direction is given as,
v_x = 75 cos (90 -30) = 38 m/s
The component of the velocity in the northerly direction will be given as,
v_y = 75 sin (90 – 30) = 65 m/s.
Question
P and R are coplanar vectors.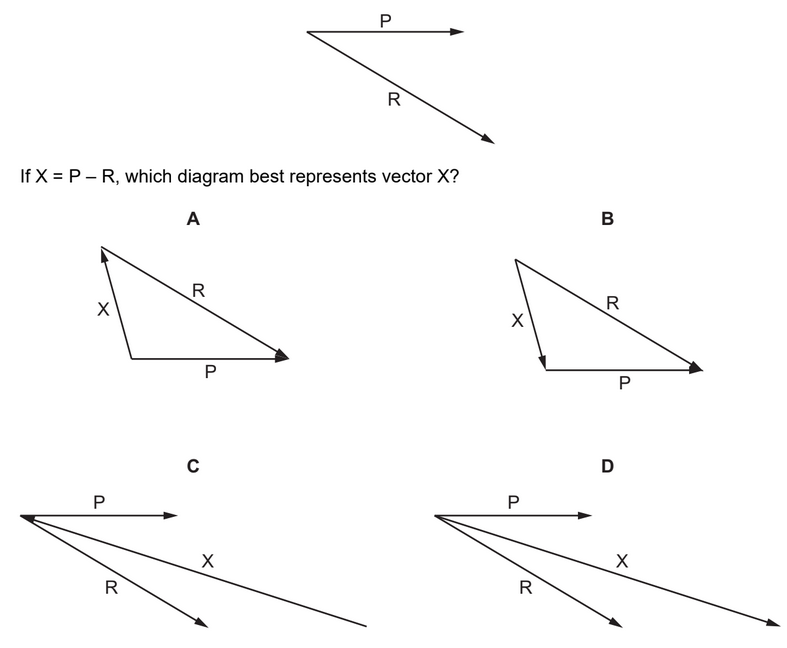
Answer/Explanation
Ans: B
From the diagram A we see that P = X -R hence
X = P +R, therefore the option is not correct.
From the diagram B we observe that,
X + R= P
hence X = P – R
therefore the option B is correct.
The diagonal will represent the sum and the negative of the sum of the two vectors therefore C and D are incorrect.
