Question
(a) Complete Table 1.1 by stating whether each of the quantities is a vector or a scalar.
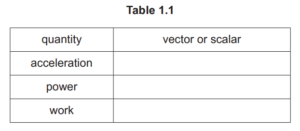
(b) The variation with time t of the velocity v of an object is shown in Fig. 1.1.
(i) Determine the acceleration of the object from time t = 0 to time t = 4.0s.
acceleration = ………………………………………… ms−2 [2]
(ii) Determine the distance moved by the object from time t = 0 to time t = 4.0s.
distance = …………………………………………….. m [2]
(c) (i) Define force. [1]
(ii) The motion represented in Fig. 1.1 is caused by a resultant force F acting on the object.
On Fig. 1.2, sketch the variation of F with time t from t = 0 to t = 12.0s. Numerical values of F are not required.
[3]
[Total: 10]
Answer/Explanation
Ans
(a) acceleration: vector
work: scalar
power: scalar
Three correct scores 2 marks. Two correct scores 1 mark.
(b) (i) a = (v –u) / t or a = gradient or a =Δv / (Δ)t
e.g. a = (1.40 – 0.70) / 4.0
= 0.18 ms–2
(b) (ii) distance = 0.5× (0.70 + 1.40)× 4.0
or
(0.70× 4.0) + (0.5× 0.70× 4.0)
= 4.2 m
(c) (i) (force equal to) rate of change of momentum
(c) (ii) horizontal line starting from t = 0 and ending at t = 4.0 s at a positive value of F
horizontal line starting from t = 4.0 s and ending
at t = 8.0 s at F = 0
horizontal line starting from t = 8.0 s and ending at t = 12.0 s at a negative value of F and the magnitude of F is larger than
from t = 0 to 4.0 s
Question
(a) State what is meant by a scalar quantity and by a vector quantity.
scalar: ……………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………………………
vector: ……………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………………………
[2]
(b) Complete Fig. 1.1 to indicate whether each of the quantities is a vector or a scalar.

(c) An aircraft is travelling in wind. Fig. 1.2 shows the velocities for the aircraft in still air and for the wind.
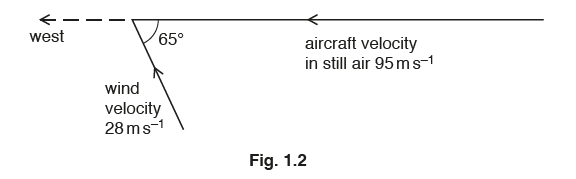
The velocity of the aircraft in still air is 95 m s–1 to the west.
The velocity of the wind is 28 m s–1 from 65° south of east.
(i) On Fig. 1.2, draw an arrow, labelled R, in the direction of the resultant velocity of the
aircraft. [1]
(ii) Determine the magnitude of the resultant velocity of the aircraft.
magnitude of velocity = …………………………………………. m s–1 [2]
Answer/Explanation
Ans:
(a) a scalar has magnitude (only)
a vector has magnitude and direction
(b) power: scalar
temperature: scalar
momentum: vector
(c)(i) arrow labelled R in a direction from 5° to 20° north of west
(c)(ii)\(v^2 = 282 + 952 – (2× 28 × 95× cos 115°)\)
or
\(v^2 = [(95 + 28cos65°)^2 + (28sin65°)^2]\)
v = 110 m s–1 (109.8 m s–1)
or (scale diagram method)
triangle of velocities drawn
v = 110 m s–1 (allow 108 –112 m s–1)