Question
(a) State Kirchhoff’s second law.
.………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(b) A battery has electromotive force (e.m.f.) 4.0V and internal resistance 0.35Ω. The battery is
connected to a uniform resistance wire XY and a fixed resistor of resistance R, as shown in
Fig. 5.1.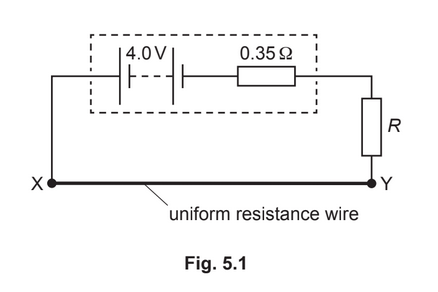
Wire XY has resistance 0.90Ω. The potential difference across wire XY is 1.8V.
Calculate:
(i) the current in wire XY
current = ……………………………………………… A [1]
(ii) the number of free electrons that pass a point in the battery in a time of 45s
number = …………………………………………………
(iii) resistance R.
R = …………………………………………….. Ω
(c) A cell of e.m.f. 1.2V is connected to the circuit in (b), as shown in Fig. 5.2.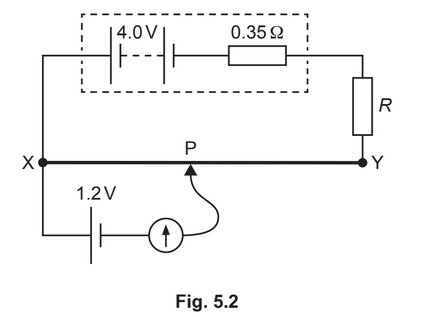
The connection P is moved along the wire XY. The galvanometer reading is zero when
distance XP is 0.30m.
(i) Calculate the total length L of wire XY.
L = …………………………………………….. m [2]
(ii) The fixed resistor is replaced by a different fixed resistor of resistance greater than R.
State and explain the change, if any, that must be made to the position of P on wire XY
so that the galvanometer reading is zero.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
Answer/Explanation
Ans:
(a) sum of e.m.f.(s) = sum of p.d.(s)
or
(algebraic) sum of e.m.f.(s) and p.d.(s) is zero
around a loop/around a closed circuit
(b)(i) I = 1.8 / 0.90= 2.0A
(b)(ii) Q =It
number \(= (2.0\times 45) / 1.60\times 10^{–19}= 5.6 \times 10^{20}\)
(b)(iii) 4.0 = 1.8 + [2.0× (0.35 +R)]
or
4.0 = 2.0× (0.90 + 0.35 +R)
R = 0.75Ω
(c)(i) 1.2 / 1.8 = 0.30 / L
L = 0.45 m
(c)(ii) p.d. across XY decreases/p.d. across XP decreases
(so) P is moved towards Y/away from X/to the right
Question
(a) State Kirchhoff’s first law. [2]
(b) The circuit shown in Fig. 5.1 contains a battery of electromotive force (e.m.f.) E and negligible
internal resistance connected to four resistors R1, R2, R3 and R4, each of resistance R.
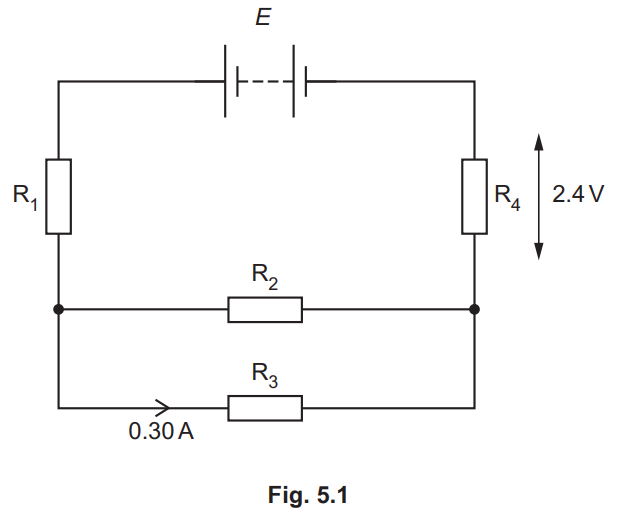
The current in R3 is 0.30A and the potential difference (p.d.) across R4 is 2.4V.
(i) Show that R is equal to 4.0Ω. [2]
(ii) Determine the e.m.f. E of the battery.
E = ……………………………………………… V [2]
(c) The battery in (b) is replaced with another battery of the same e.m.f. E but with an internal
resistance that is not negligible.
State and explain the change, if any, in the total power produced by the battery. [2]
(d) The resistors in the circuit of Fig. 5.1 are made from nichrome wire of uniform radius 240μm.
The length of this wire needed to make each resistor is 0.67m.
Calculate the resistivity of nichrome.
resistivity = ………………………………………….. Ωm [3]
[Total: 11]
Answer/Explanation
(a) sum of current(s) in = sum of current(s) out
or
(algebraic) sum of current(s) is zero
at a junction (in a circuit) A1
(b) (i) (current in R4 or R1 =) 0.30 + 0.30
(= 0.60A)
(R =) 2.4 / 0.60 = 4.0 (Ω) A1
or
(p.d. across R3 or R2 =) 2.4 / 2
(= 1.2 V)
(R =) 1.2 / 0.30 = 4.0 (Ω)
(b) (ii) E = 2.4 + 2.4 + 1.2 C1
= 6.0 V A1
or
total resistance = 10 (Ω)
E = 10 × 0.60 = 6.0 V
(c) total resistance increases
current decreases (in battery) so total power decreases
(d) resistivity = RA / L
= 4.0 × π × (240 × 10–6)2 / 0.67
= 1.1 × 10–6 Ω m
