Question
(a) With reference to velocity and acceleration, describe uniform circular motion. [2]
(b) Two cars are moving around a horizontal circular track. One car follows path X and the other follows path Y, as shown in Fig. 1.1.
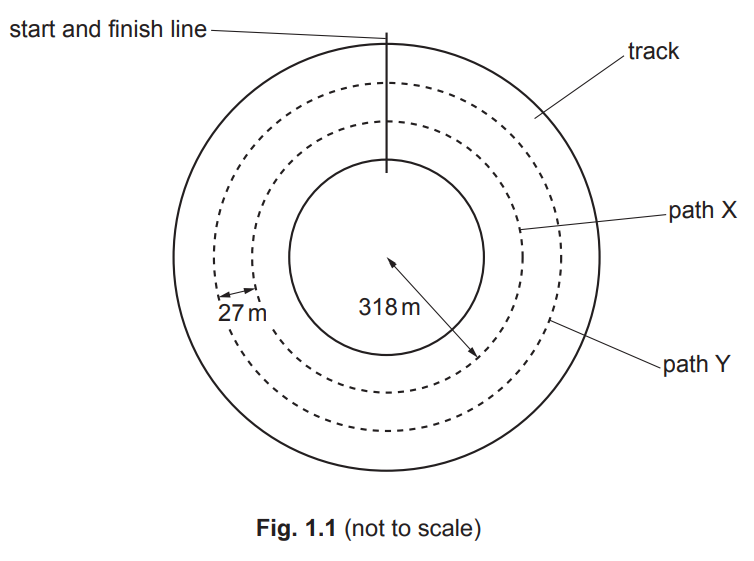
The radius of path X is 318m. Path Y is parallel to, and 27m outside, path X. Both cars have mass 790kg. The maximum lateral (sideways) friction force F that the cars can experience without sliding is the same for both cars.
(i) The maximum speed at which the car on path X can move around the track without sliding is 94ms–1.
Calculate F
(ii) Both cars move around the track. Each car has the maximum speed at which it can move without sliding.
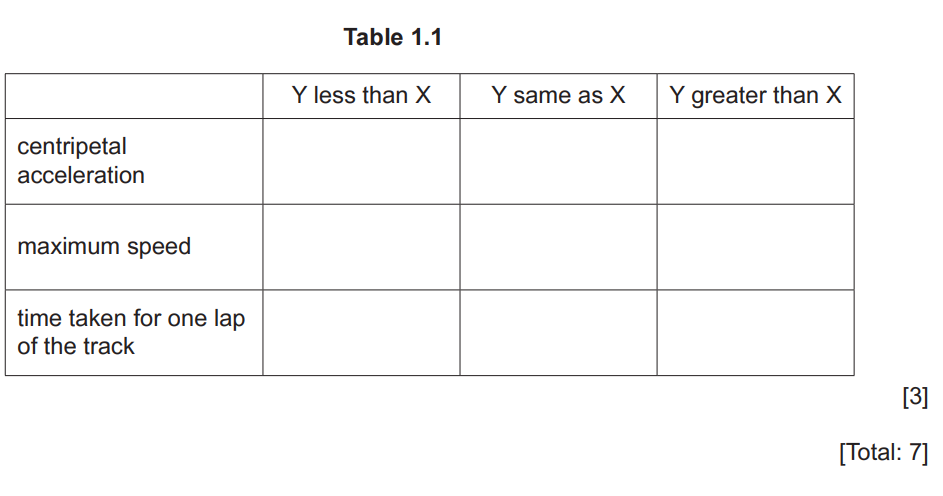
Complete Table 1.1, by placing one tick in each row, to indicate how the quantities indicated for the car on path Y compare with the car on path X
Answer/Explanation
Ans
(a) constant speed or constant magnitude of velocity
acceleration (always) perpendicular to velocity
(b) (i) \(F = mv^2 / r\)
or
v = rω and F = mrω2
F = 790 × 942 / 318
= 22000 N
(b) (ii) centripetal acceleration: same
maximum speed: greater
Question
(a) State what is meant by a gravitational force.
(b) A binary star system consists of two stars \(S_1\) and \(S_2\), each in a circular orbit.
The orbit of each star in the system has a period of rotation T.
Observations of the binary star from Earth are represented in Fig. 1.1.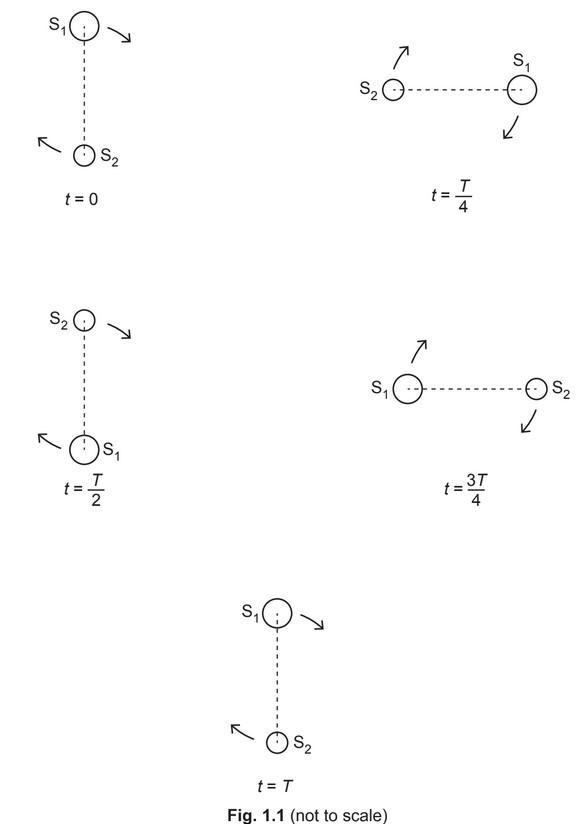
Observed from Earth, the angular separation of the centres of \(S_1\) and \(S_2\) is \(1.2 × 10^{–5}\) rad.
The distance of the binary star system from Earth is \(1.5 × 10^{17}\)m.
Show that the separation d of the centres of \(S_1\) and \(S_2\) is \(1.8 × 10^{12}\)m.
(c) The stars \(S_1\) and \(S_2\) rotate with the same angular velocity ω about a point P, as illustrated in
Fig. 1.2.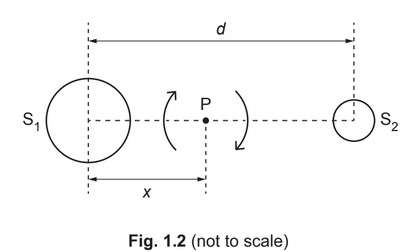
Point P is at a distance x from the centre of star \(S_1\).
The period of rotation of the stars is 44.2 years.
(i) Calculate the angular velocity ω.
ω = ………………………………………. \(rads^{–1}\)
(ii) By considering the forces acting on the two stars, show that the ratio of the masses of the stars is given by
\(\frac{mass of S_1}{mass of S_2} = \frac{d-x}{x}\)
(iii) The mass \(M_1\) of star \(S_1\) is given by the expression
\(GM_1 = d^2 (d – x)ω^2\)
where G is the gravitational constant.
The ratio in (ii) is found to be 1.5.
Use data from (b) and your answer in (c)(i) to determine the mass \(M_1\).
\(M_1\) = ……………………………………………. kg
Answer/Explanation
Answer:
(a) force acting between two masses
or
force on mass due to another mass
or
force on mass in a gravitational field
(b) arc length = rθ
\(d = 1.5 × 10^{17} × 1.2 × 10^{–5} = 1.8 × 10^{12}\) m
(c) (i) ω = 2 π / T
= 2 π / (44.2 × 365 × 24 × 3600)
\(= 4.5 × 10^{–9} rad s^{–1}\)
(ii) gravitational forces are equal
or
centripetal force about P is the same
\(M_1xω^2 = M_2(d – x)ω^2\) so \(M_1 / M_2 = (d – x) / x\)
(iii) x = 0.4d
\(6.67 × 10^{–11} × M1 = (1.0 – 0.4) × (1.8 × 10^{12})^3 × (4.5 × 10–9)^2\)