Question
(a) The point P in Fig. 1.1 represents a point mass.
On Fig. 1.1, draw lines to represent the gravitational field around P.

Fig. 1.1
(b) A moon is in circular orbit around a planet.
Explain why the path of the moon is circular.
(c) Many moons are in circular orbit about a planet.
The angular velocity of a moon is ω when the orbit of the moon has a radius r about the planet.
Fig. 1.2 shows the variation of \(r^{3}\) with \(1/ω^{2}\) for these moons.
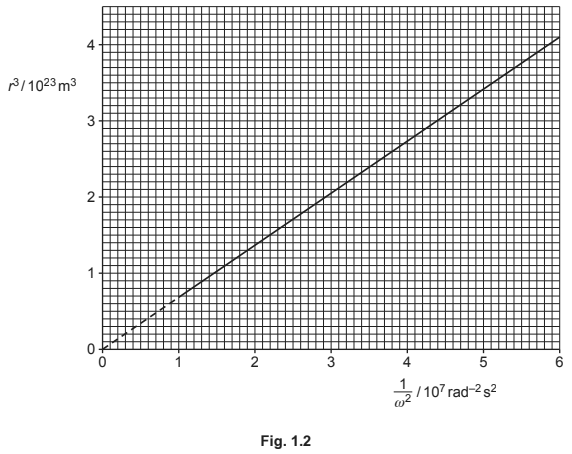
(i) Show that the mass M of the planet is given by the expression
\(M = \frac{gradient}{G}\)
where G is the gravitational constant.
(ii) Use Fig. 1.2 and the expression in (c)(i) to show that the mass M of the planet is \(1.0 \times 10^{26}\) kg.
(iii) Determine the speed of a moon in orbit around the planet with an orbital radius of \(1.2 \times 10^{8}\)m.
Answer/Explanation
Ans:
(a) at least \(4\) straight radial lines to P

all arrows pointing along the lines towards P
(b) Any 2 from:
gravitational force provides the centripetal force
(centripetal or gravitational) force has constant magnitude
(centripetal or gravitational) force is perpendicular to velocity (of moon) / direction of motion (of moon)
(c) (i) \(\frac{GMm}{r^{2}}\) = \(mr\omega ^{2}\)
\(M\) = \(\frac{r^{3}\omega ^{2}}{G}\) and gradient = \(r^{2}\omega ^{2}\) hence M = \(\frac{gradient}{G}\)
or
\(r^{3}\) = \(GM \times 1/\omega ^{2}\) so gradient = GM hence M = \(\frac{gradient}{G}\)
(ii) \(M = 4.1\times 10^{23}/(6.0 \times 10^{7}\times 6.67\times 10^{-11})\) = \(1.0 \times 10^{26}\) kg
(iii) \(\frac{GMm}{r^{2}}\) = \(\frac{mv^{2}}{r}\)
\(\frac{GM}{r}\) = \(v^{2}\)
\(v^{2}\) = \(\frac{6.67\times 10^{-11}\times 1.0\times 10^{26}}{1.2\times 10^{8}}\)
\(v^{2}\) = \(5.6 \times 10^{7}\, ms^{-1}\)
Question
(a) Define gravitational potential. [2]
(b) The Earth E and the Moon M can both be considered as isolated point masses at their centres. The mass of the Earth is 5.98 × 1024 kg and the mass of the Moon is 7.35 × 1022 kg. The Earth and the Moon are separated by a distance of 3.84 × 108m, as shown in Fig. 2.1.
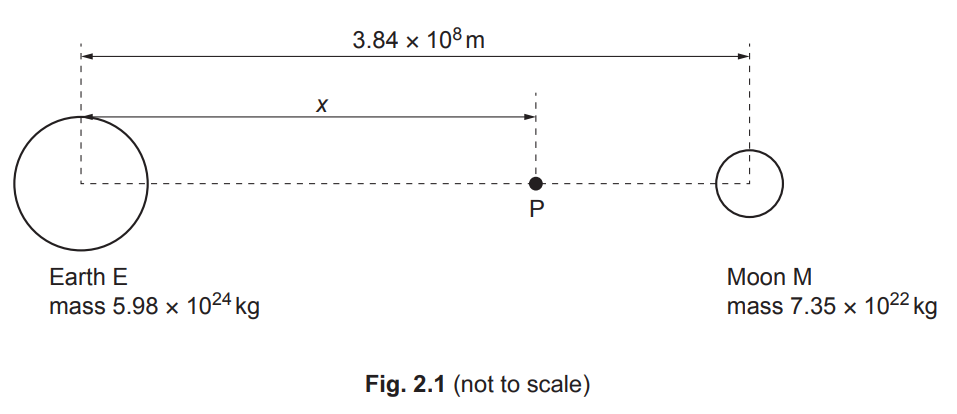
P is a point, on the line joining the centres of E and M, where the resultant gravitational field strength is zero. Point P is at a distance x from the centre of the Earth.
(i) Explain how it is possible for the gravitational field strength to be zero despite the presence of two large masses nearby. [2]
(ii) Show that x is approximately 3.5 × 108m. [2]
(iii) Calculate the gravitational potential φ at point P.
φ = ……………………………………….. J kg–1 [3]
[Total: 9]
Answer/Explanation
Ans
(a) work done per unit mass
(work done in) moving mass from infinity
(b) (i) (gravitational) fields from the Earth and Moon are in opposite directions
(resultant is zero where gravitational) fields are equal (in magnitude)
(b) (ii) \(g\infty M/r^{2}\)
5.98 × 1024 / x2 = 7.35 × 1022 / (3.84 × 108 – x)2
leading to x = 3.5 × 108 (m)
(b) (iii) φ (Earth) = (–)6.67 × 10–11 × (5.98 × 1024 / 3.5 × 108)
and
φ (Moon) = (–)6.67 × 10–11 × (7.35 × 1022 / 0.38 × 108)
φ = (–)6.67 × 10–11 × [(5.98 × 1024 / 3.5 × 108) + (7.35 × 1022 / 0.38 × 108)]
= – 1.3 × 106 J kg
