Question
(a) Define gravitational potential. [2]
(b) The Earth E and the Moon M can both be considered as isolated point masses at their centres. The mass of the Earth is 5.98 × 1024 kg and the mass of the Moon is 7.35 × 1022 kg. The Earth and the Moon are separated by a distance of 3.84 × 108m, as shown in Fig. 2.1.
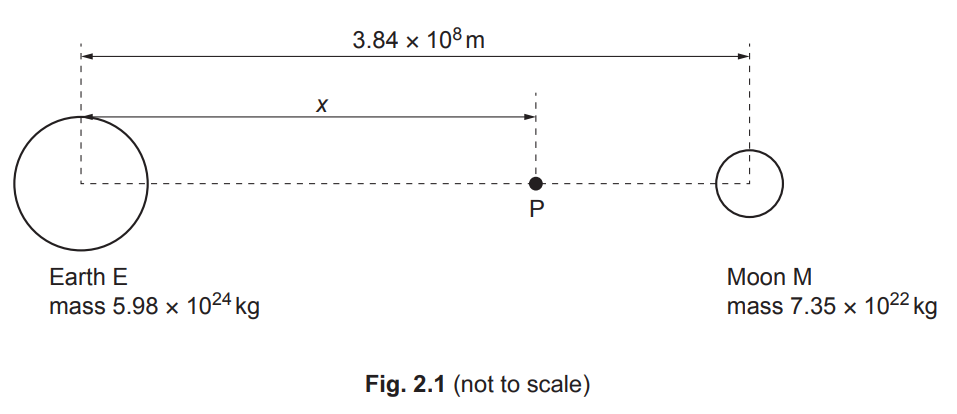
P is a point, on the line joining the centres of E and M, where the resultant gravitational field strength is zero. Point P is at a distance x from the centre of the Earth.
(i) Explain how it is possible for the gravitational field strength to be zero despite the presence of two large masses nearby. [2]
(ii) Show that x is approximately 3.5 × 108m. [2]
(iii) Calculate the gravitational potential φ at point P.
φ = ……………………………………….. J kg–1 [3]
[Total: 9]
Answer/Explanation
Ans
(a) work done per unit mass
(work done in) moving mass from infinity
(b) (i) (gravitational) fields from the Earth and Moon are in opposite directions
(resultant is zero where gravitational) fields are equal (in magnitude)
(b) (ii) \(g\infty M/r^{2}\)
5.98 × 1024 / x2 = 7.35 × 1022 / (3.84 × 108 – x)2
leading to x = 3.5 × 108 (m)
(b) (iii) φ (Earth) = (–)6.67 × 10–11 × (5.98 × 1024 / 3.5 × 108)
and
φ (Moon) = (–)6.67 × 10–11 × (7.35 × 1022 / 0.38 × 108)
φ = (–)6.67 × 10–11 × [(5.98 × 1024 / 3.5 × 108) + (7.35 × 1022 / 0.38 × 108)]
= – 1.3 × 106 J kg
Question
(a) State Newton’s law of gravitation. [2]
(b) Planets have been observed orbiting a star in another solar system. Measurements are made
of the orbital radius r and the time period T of each of these planets.
The variation with R3 of T2 is shown in Fig. 1.1.
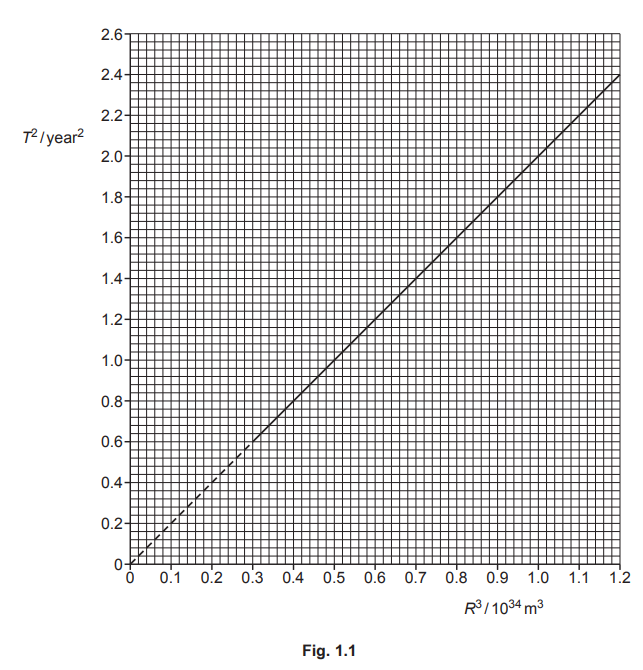
The relationship between T and R is given by
\(T^{2}=\frac{4\pi ^{2}R^{3}}{GM}\)
where G is the gravitational constant and M is the mass of the star.
Determine the mass M.
M = ……………………………………………. kg [3]
(c) A rock of mass m is also in orbit around the star in (b). The radius of the orbit is r.
(i) Explain why the gravitational potential energy of the rock is negative. [3]
(ii) Show that the kinetic energy Ek of the rock is given by
\(E_{k}=\frac{GMm}{2r}\) [2]
(iii) Use the expression in (c)(ii) to derive an expression for the total energy of the rock. [2]
[Total: 12]
Answer/Explanation
Ans
(a) (gravitational) force is (directly) proportional to product of masses
force (between point masses) is inversely proportional to the square of their separation
(b) correct read offs from the graph with correct power of ten for R3
\(M=\frac{4\times \pi ^{2}\times 1.2\times 10^{34}}{6.67\times 10^{-11}\times 2.4\times \left ( 365\times 24\times 3600 \right )^{2}}\)
= × 3.0 1030 kg
(c) (i) potential energy is zero at infinity
(gravitational) forces are attractive
work must be done on the rock to move it to infinity
(c) (ii) \(\frac{GMm}{r^{2}}=\frac{mv^{2}}{r} \\) OR\(\ v^{2}=\frac{GM}{r} \ OR\ v=\sqrt{\frac{GM}{r}}\)
use of \(½ mv^2\) (e.g. multiplication by ½ m) leading to \(\frac{GMm}{r^{2}}\)
(c)(iii) \(E_p=φ m \\) and \(\ φ =\frac{-GM}{r}\) \ or\ \(E_{p}=\frac{-GMm}{r}\)
Total energy = Ek + Ep
