Question
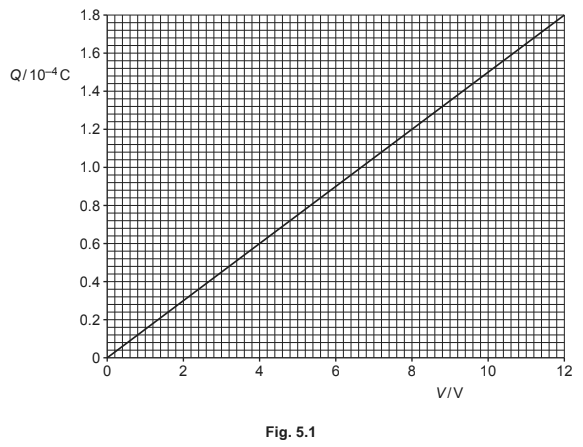
The variation with potential difference V of the charge Q on one of the plates of a capacitor is shown in Fig. 5.1.
The capacitor is connected to an 8.0V power supply and two resistors R and S as shown in Fig. 5.2.
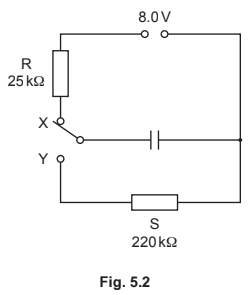
The resistance of R is \(25\) kΩ and the resistance of S is \(220\) kΩ.
The switch can be in either position X or position Y.
(a) The switch is in position X so that the capacitor is fully charged.
Calculate the energy E stored in the capacitor.
(b) The switch is now moved to position Y.
(i) Show that the time constant of the discharge circuit is \(3.3\)s.
(ii) The fully charged capacitor in (a) stores energy E.
Determine the time t taken for the stored energy to decrease from E to E/9
(c) A second identical capacitor is connected in parallel with the first capacitor.
State and explain the change, if any, to the time constant of the discharge circuit.
Answer/Explanation
Ans:
(a) (energy stored =) area under line or \(1/2\) QV
= \(1/2 \times 8.0 \times 1.2 \times 10^{-4}\)
= \(4.8 \times 10^{–4}\) J
(b) (i) (τ=) RC
(τ=) \(220 \times 10^{3} \times (1.2 \times 10^{-4}/8.0)\) = \(3.3\) s
(ii) \(E\) ∝ \(V^{2}\)
(so time to) \(V_{0}/3\)
\(V\) = \(V_{0}e^{-t/RC}\)
\(\frac{V_{0}}{3}\) = \(V_{0}e^{-t/3.3}\)
\(\frac{1}{3}\) = \(e^{-t/3.3}\)
\(t\) = \(3.6\) s
(c) (total) capacitance is doubled
Question
(a) A capacitor consists of two parallel metal plates, separated by air, at a variable distance x apart, as shown in Fig. 6.1. The capacitance C is inversely proportional to x.
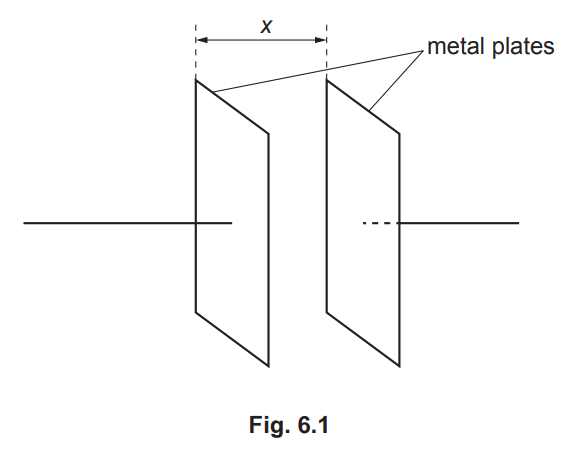
The capacitor is charged by a supply so that there is a potential difference (p.d.) V between the plates. State expressions, in terms of C and V, for the charge Q on one of the plates and for the
energy E stored in the capacitor.
Q = ……………………………………… E = ……………………………………… [1]
(b) The charged capacitor in (a) is now disconnected from the supply. The plates of the capacitor are initially separated by distance L. They are then moved closer together by a distance D, as
shown in Fig. 6.2.
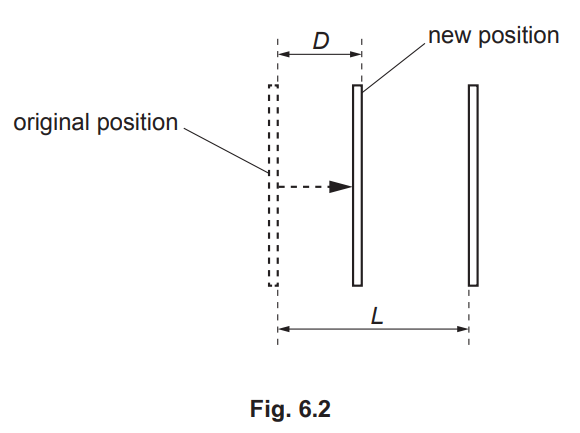
State expressions, in terms of C, V, L and D, for:
(i) the new capacitance CN
CN = ………………………………………………… [1]
(ii) the new charge QN on one of the plates
QN = ………………………………………………… [1]
(iii) the new p.d. VN between the plates.
VN = ………………………………………………… [1]
(c) Explain whether reducing the separation of the plates in (b) results in an increase or decrease in the energy stored in the capacitor. [1] [Total: 5]
Answer/Explanation
Ans
(a) Q = CV and E = ½CV2
(b) (i) CN = CL / (L – D)
(b) (ii) (charge is unchanged by moving the plates so) QN = CV
(b) (iii) VN = QN / CN
= (CV) / [CL / (L – D)]
=V(L – D) / L
