Question
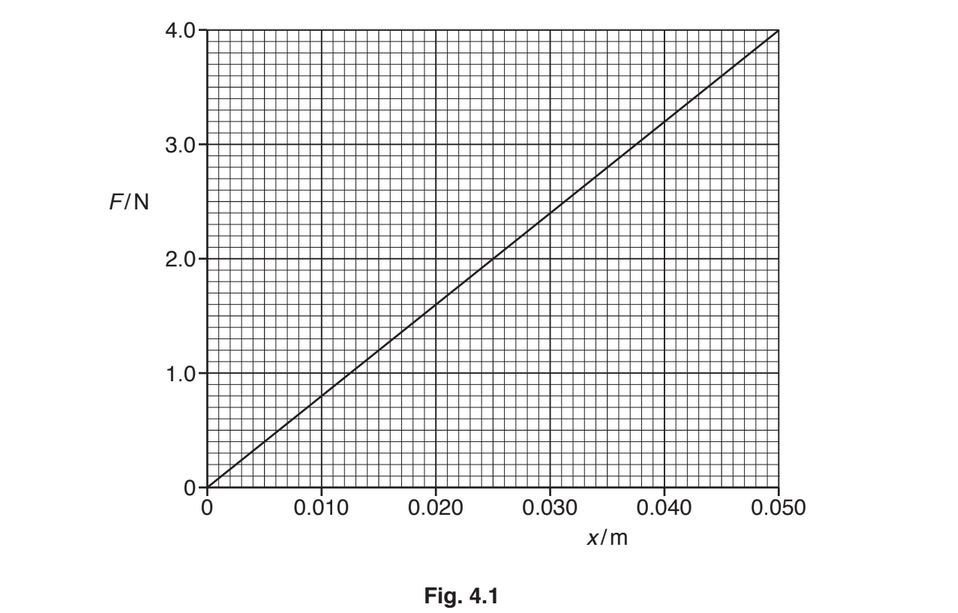
The variation with extension x of the force F applied to a spring is shown in Fig. 4.1.
The spring has an unstretched length of 0.080 m and is suspended vertically from a fixed point, as shown in Fig. 4.2.
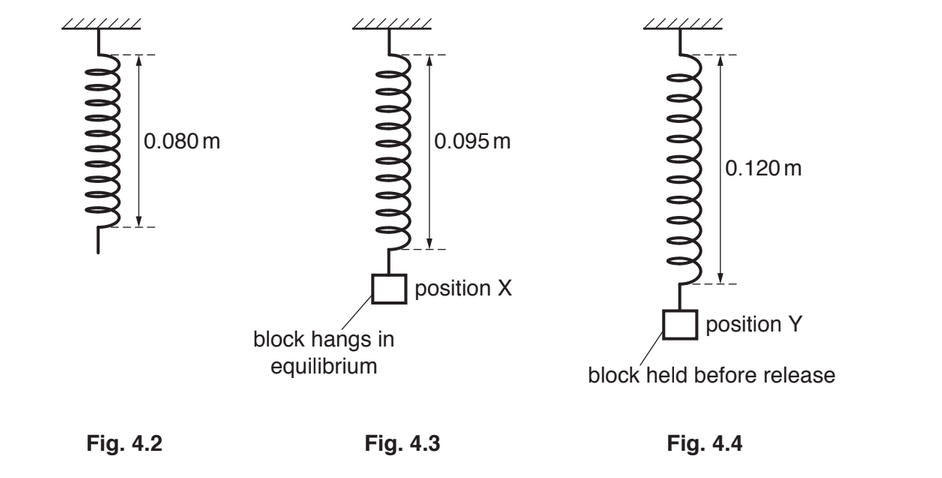
A block is attached to the lower end of the spring. The block hangs in equilibrium at position X when the length of the spring is 0.095m, as shown in Fig. 4.3. The block is then pulled vertically downwards and held at position Y so that the length of the spring is 0.120m, as shown in Fig. 4.4. The block is then released and moves vertically upwards from position Y back towards position X.
(a) Use Fig. 4.1 to determine the spring constant of the spring.
spring constant = ……………………………………….. \(Nm^{–1}\) [2]
(b) Use Fig.4.1 to show that the decrease in elastic potential energy of the spring is 0.055J when the block moves from position Y to position X. [2]
(c) The block has a mass of 0.122kg. Calculate the increase in gravitational potential energy of the block for its movement from position Y to position X.
increase in gravitational potential energy = ……………………………………………… J [2]
(d) Use the decrease in elastic potential energy stated in (b) and your answer in (c) to determine, for the block, as it moves through position X:
(i) its kinetic energy
kinetic energy = ……………………………………………… J [1]
(ii) its speed.
speed = ………………………………………… \(ms^{–1}\) [2] [Total: 9]
Answer/Explanation
Ans:
(a) \(k =F / x\) or k = gradient
e.g. \(k = 4.0 / 0.050\)
\(k = 80N m^{–1}\)

(d)(i) E = 0.055 – 0.030
= 0.025 J
(d)(ii) \(E = 1⁄2mv^2\)
\(v = [(2× 0.025) / 0.122]0.5= 0.64m /s\)
Question
(a) State Hooke’s law. [1]
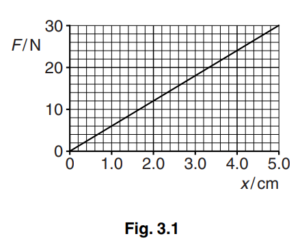
(b) The variation with compression x of the force F acting on a spring is shown in Fig. 3.1.
The spring is fixed to the closed end of a horizontal tube. A block is pushed into the tube so
that the spring is compressed, as shown in Fig. 3.2.
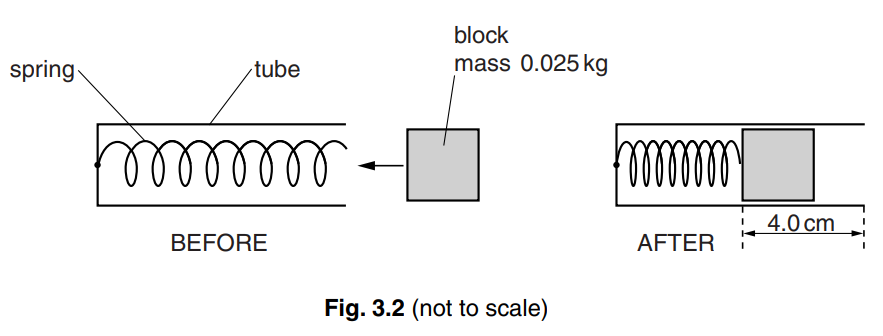
The compression of the spring is 4.0 cm. The mass of the block is 0.025 kg.
(i) Calculate the spring constant of the spring.
spring constant = ………………………………………… N m–1 [2]
(ii) Show that the work done to compress the spring by 4.0 cm is 0.48 J. [2]
(iii) The block is now released and accelerates along the tube as the spring returns to its
original length. The block leaves the end of the tube with a speed of 6.0 m s–1.
1. Calculate the kinetic energy of the block as it leaves the end of the tube.
kinetic energy = ………………………………………………. J [2]
2. Assume that the spring has negligible kinetic energy as the block leaves the tube.
Determine the average resistive force acting against the block as it moves along the
tube.
resistive force = ……………………………………………… N [3]
(iv) Determine the efficiency of the transfer of elastic potential energy from the spring to the
kinetic energy of the block.
efficiency = …………………………………………………. [2]
[Total: 12]
Answer/Explanation
Ans
(a) force/load is proportional to extension/compression (provided proportionality limit
is not exceeded)
(b) (i) k = F/ x or k = gradient
k = 600N m–1
(ii) (W =) ½kx2 or (W =) ½Fx or (W =) area under graph
(W =) 0.5 × 600 × (0.040)2= 0.48 J or (W =) 0.5 × 24 × 0.040 = 0.48
(iii) 1. (EK =) ½mv2
= ½ × 0.025 × 6.02
= 0.45 J
(iii) 2. (work done against resistive force =) 0.48 – 0.45 [= 0.03(0)J] C1
average resistive force = 0.030 / 0.040
= 0.75N
(iv) efficiency = [useful energy out / total energy in] (×100)
= [0.45 / 0.48] (×100)
= 0.94 or 94%
