Question
(a) (i) State the conditions required for the formation of a stationary wave.
……………………………………………………………………………………………. [2]
(ii) State the phase difference between any two vibrating particles in a stationary wave between two adjacent nodes.
phase difference = ………………………………………………..° [1]
(b) A motorcycle is travelling at 13.0 m/s along a straight road. The rider of the motorcycle sees a pedestrian standing in the road directly ahead and operates a horn to emit a warning sound.
The pedestrian hears the warning sound from the horn at a frequency of 543Hz. The speed of the sound in the air is 334 m/s.
(i) Calculate the frequency, to three significant figures, of the sound emitted by the horn.
frequency = ……………………………………………. Hz [2]
(ii) The motorcycle rider passes the stationary pedestrian and then moves directly away from her. As the rider moves away, he operates the horn for a second time. The pedestrian now hears sound that is increasing in frequency.
State the variation, if any, in the speed of the motorcycle when the rider operates the horn for the second time…………………………………… [1]
(c) A beam of vertically polarised monochromatic light is incident normally on a polarising filter, as shown in Fig. 5.1.
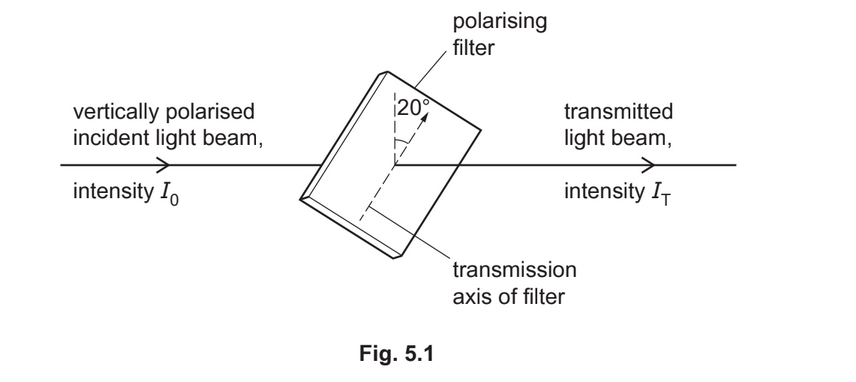
The filter is positioned with its transmission axis at an angle of 20° to the vertical. The incident light has intensity \(I_0\) and the transmitted light has intensity \(I_T\).
(i) By considering the ratio \(\frac{I_T}{I_0}\) calculate the ratio 
Show your working. ratio = ………………………………………………… [3]
(ii) The filter is now rotated, about the direction of the light beam, from its starting position shown in Fig. 5.1. The direction of rotation is such that the angle of the transmission axis to the vertical initially increases.
Calculate the minimum angle through which the filter must be rotated so that the intensity of the transmitted light returns to the value that it had when the filter was at its starting position.
angle = ………………………………………………. ° [1]
Answer/Explanation
Ans:
(a)(i) (two) waves travelling (at same speed) in opposite directions overlap waves (of the same type) have same frequency/wavelength
(a)(ii) phase difference = 0

Question
(a) State the difference between a stationary wave and a progressive wave in terms of
(i) the energy transfer along the wave,
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
(ii) the phase of two adjacent vibrating particles.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
(b) A tube is open at both ends. A loudspeaker, emitting sound of a single frequency, is placed near one end of the tube, as shown in Fig. 3.1.
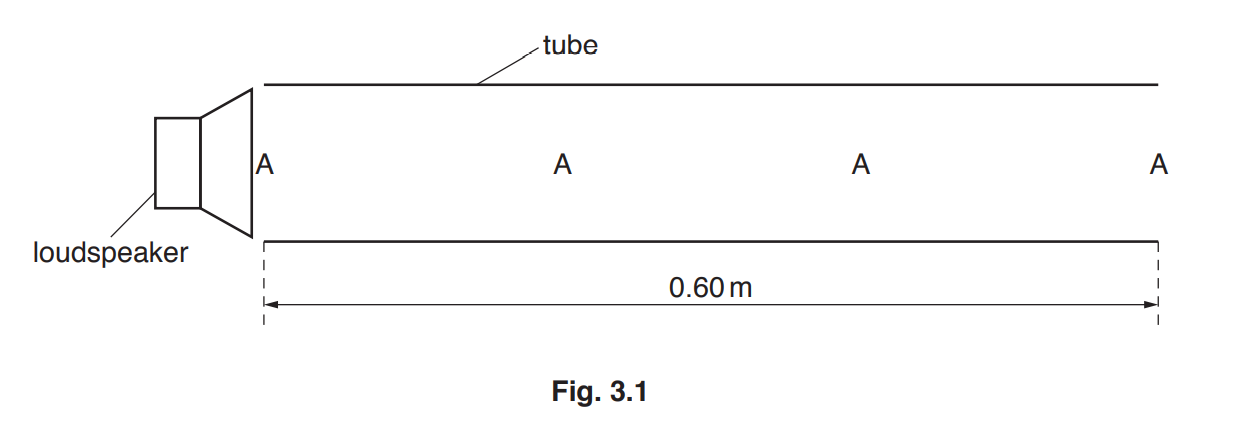
The speed of the sound in the tube is 340m/s. The length of the tube is 0.60m.
A stationary wave is formed with an antinode A at each end of the tube and two antinodes inside the tube.
(i) State what is meant by an antinode of the stationary wave.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
(ii) State the distance between a node and an adjacent antinode.
distance = ……………………………………………… m
(iii) Determine, for the sound in the tube,
1.
the wavelength,
wavelength = ……………………………………………… m
2.
the frequency.
frequency = ……………………………………………. Hz
(iv) Determine the minimum frequency of the sound from the loudspeaker that produces a stationary wave in the tube.
minimum frequency = ……………………………………………. Hz
Answer/Explanation
(a)(i)
in a stationary wave energy is not transferred
or
in a progressive wave energy is transferred
(a)(ii)
in a stationary wave (adjacent) particles are in phase
or
in a progressive wave (adjacent) particles are out of phase/have a phase difference/not in phase
(b)(i)
(position where) maximum amplitude
(b)(ii)
distance = 0.10 m
(b)(iii) 1.
λ = 0.60/1.5
= 0.40m
(b)(iii) 2.
v = fλ
f = 340/0.40
= 850Hz
(b)(iv)
λ = 2 × 0.60 or λ = 3 × 0.40 or f = 850/3
f = 280 (283) Hz
