Types of electric current
- Direct Current (D.C.): Flow of charges in the circuit is in the same direction all the time, from a higher potential to a lower potential (e.g. current from battery).
- Alternating Current: Flow of charges in the circuit reverses direction at regular intervals (e.g. current from household mains).
Electric circuits consist of circuit components (e.g. batteries, resistors, and switches) connected by conductors (e.g. copper cables).
For electric current to flow, the circuit components and conductors must form closed loops. There must also be sources of electrical energy (e.g. batteries) and sinks of electrical energy among the circuit components (e.g. resistors and lamps).
Note : This chapter includes only D.C. In AS syllabus A.C is not included.
Electrical Circuit Symbols
Circuit symbols:Electrical circuits use a lot of components and when circuits are drawn their symbols are used the following are the standered symbols used in circuits:-
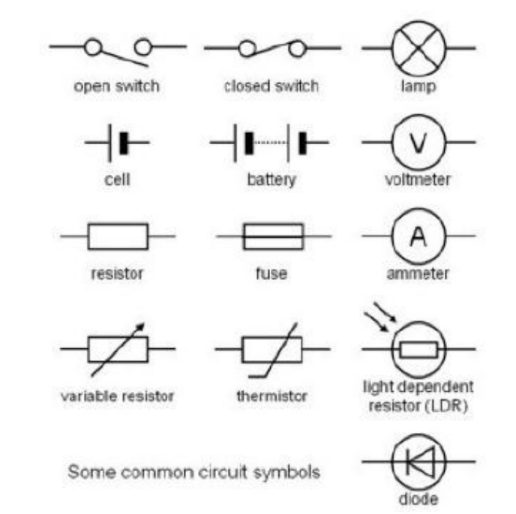
Figure : Symbols of common circuit elements
Draw and interpret circuit diagrams containing sources, switches, resistors, ammeters, voltmeters, and/or any other type of component
Note that, for a certain electric circuit, there are different ways of drawing its circuit diagram.
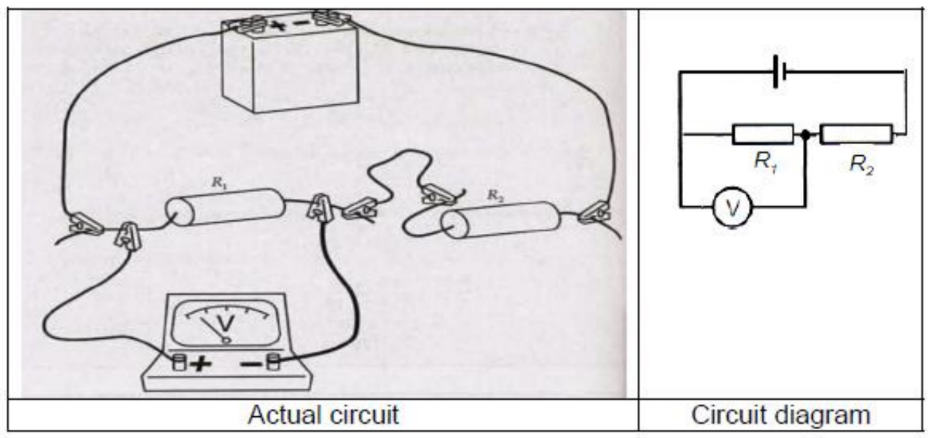
Two other possible circuit diagrams for the above electric circuit are as follows:
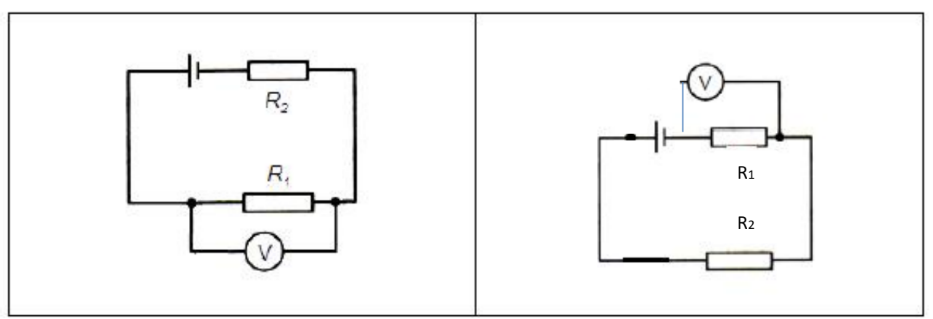
Example 1: Draw the circuit diagram for the electric circuit shown below.
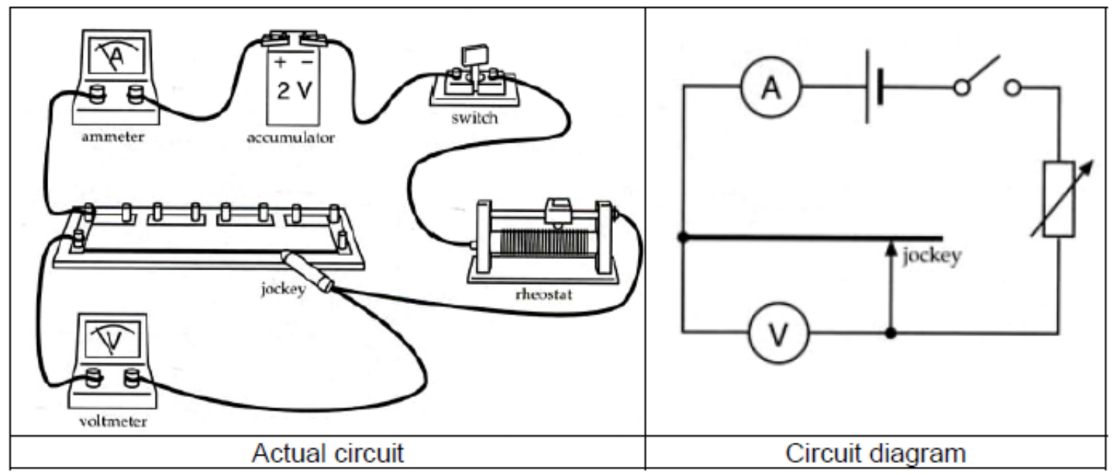
COMBINATION OF RESISTORS- RESISTANCE IN SERIES AND PARALLEL
Resistors connected in Series
RESISTORS CONNECTED IN SERIES:-The figure below shows 3 resistors connected in series to an Ideal battery (no internal resistance) Connection in series means the resistors are wired one after the other and the potential difference $\mathrm{V}$ is applied across the ends of the whole series.
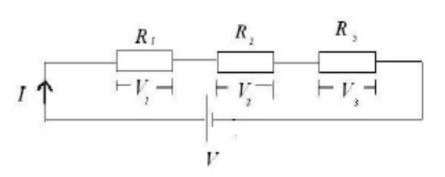
Figure : Resistors in series-Note the current through all the resistors is the same but voltage is not
When a potential difference $\mathrm{V}$ is applied across the series the current through all the resistors is the same, but the potential difference across each resistor is different and the sum of these individual
potential differences is equal to the applied potential difference $\mathrm{V}$
$
\begin{array}{r}
V_1=I R_1 \\
V_2=I R_2 \\
V_3=I R_3 \\
V=V_1+V_2+V_3 \\
V=I R_1+I R_2+I R_3 \\
V=I\left(R_1+R_2+R_3\right) \\
\frac{V}{I}=R_{e q}=R_1+R_2+R_3
\end{array}
$
Hence the equivalent resistance of a series combination is given by
$
R_{e q}=R_1+R_2+R_3
$
In general if there are $\mathrm{n}$ resistors connected in series then
$
R_{e q}=R_1+R_2+R_3 \ldots R_n
$
IN SERIES
- The resistors connected in series can be replaced by an equivalent resistor $R_{e q}$
- $R_{e q}$ has the same current I as the individual resistors
- Two resistors are said to be connected series if current can flow from one resistor to another without branching
RESISTORS CONNECTED IN PARALLEL:-
The figure below shows 3 resistors connected in parallel to an Ideal battery (no internal resistance) Connection in parallel means the resistors are wired directly together on one side and directly together on the other side and connected sides. When resistors are connected in parallel all resistors have the same potential difference $\mathrm{V}$ as $t$ P.D. is same but current is not)
The total current in the circuit is the sum of the individual currents hence
$\begin{array}{r}I=I_1+I_2+I_3 \\ \frac{V}{R_{e q}}=\frac{V}{R_1}+\frac{V}{R_2}+\frac{V}{R_3} \\ \frac{V}{R_{e q}}=V\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)\end{array}$
Canceling V we get
$
\frac{1}{R_{e q}}=\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\right)
$
In general if there are $n$ resistors connected in parallel then:-
$
\frac{1}{R_{e q}}=\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \ldots \frac{1}{R_n}\right)
$
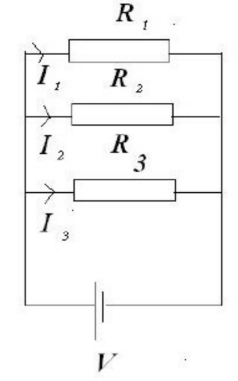
Figure : Resistance in Parellel-Note that the current branches out but voltage is the same for all 3 resistors
IN PARALLEL:-
- The resistors connected in Parallel can be replaced by an equivalent resistor $R_{e q}$
- $R_{\text {eq }}$ has the same current $\mathrm{V}$ as the individual resistors
- For resistors connected Parallel current in each of them is different but the voltage is the same
Solve problems using the formula for the combined resistance of two or more resistors in series.
Example 4
Calculate the effective resistance of a $4 \Omega$ and two $3 \Omega$ resistors connected in series.
Answer/Explanation
Solution:
$
R_{\text {eff }}=4+(2)(3)=10 \Omega
$
Example 5
Calculate the effective resistance of a $2 \Omega$, a $3 \Omega$ and a $4 \Omega$ resistor connected in parallel.
Answer/Explanation
Solution:
$
\begin{aligned}
& \frac{1}{R_{e f f}}=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{6+4+3}{12}=\frac{13}{12} \\
& R_{e f f}=0.903 \Omega \\
&
\end{aligned}
$
Why the current is the same in all series resistances? And why the voltage is the same in all parallel resistors?
(1) In a series circuit of resistors, the same current flows through all the resistors, however potential gets divided according to individual resistance values. Because according to Ohm’s law $V=I R$, and here since $I$ is same, and $V$ is directly proportional to R. Hence the potential will be different across different resistors.
(Note : Theoretically, for resistors that have equal resistance, they have same $V$ ).
(2) In the case of parallel combination of resistors, the same potential will exist across every resistor, but now current gets divided in the inverse ratio of resistance values. $(I=V / R)$ this is also in accordance with Ohm’s law.
Recap……..
Conservation of charge:The net charge of an isolated system remains constant.Charge cannot be created and destroyed, but only in positive-negative pairs.
- It is not possible to destroy or create charge.
- You can cancel out the effect of a charge(or neutralize the charge on the body) on a body by adding an equal and opposite charge to it, but you can’t destroy the charge itself.
The following example makes this clear
If a glass rod is rubbed with a silk cloth, due to friction the glass gets charged positively and the silk negatively. The charging is basically due to the transfer of negative charge(electrons) from the glass to the silk.This experiment suggests that:-
- Charge is transfered but not created or destroyed.
- The total charge on the Glass silk cloth system remains the same i.e zero before rubbing and after rubbing.