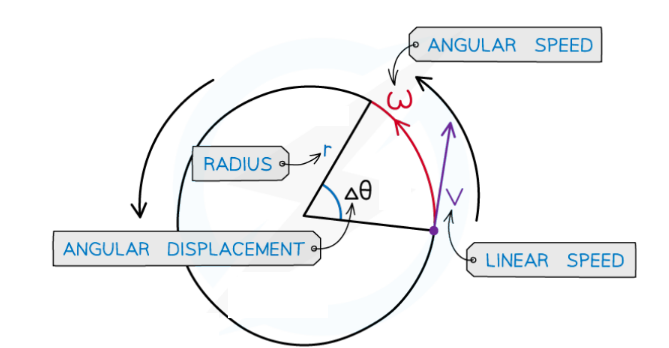
Radians & Angular Displacement
- In circular motion, it is more convenient to measure angular displacement in units of radians rather than units of degrees
- The angular displacement $(\theta)$ of a body in circular motion is defined as:
- The change in angle, in radians, of a body as it rotates around a circle
- The angular displacement is the ratio of:
$
\Delta \theta=\frac{\text { distance travelled around the circle }}{\text { radius of the circle }}
$
- Note: both distances must be measured in the same units e.g. metres
- A radian $(r a d)$ is defined as:
- The angle subtended at the centre of a circle by an arc equal in length to the radius of the circle
- Angular displacement can be calculated using the equation:
$
\Delta \theta=\frac{\Delta s}{r}
$
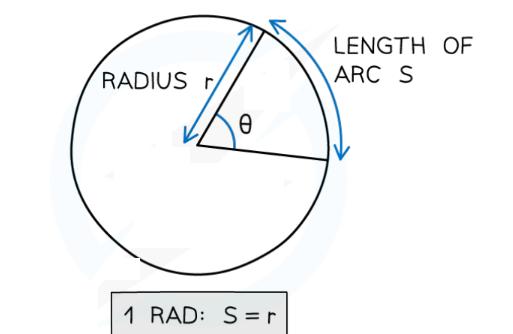
When the angle is equal to one radian, the length of the arc (Δs) is equal to the radius (r) of the circle
Where:
- Δθ = angular displacement, or angle of rotation (radians)
- s = length of the arc, or the distance travelled around the circle (m)
- r = radius of the circle (m)
- Radians are commonly written in terms of $\pi$
- The angle in radians for a complete circle $\left(360^{\circ}\right)$ is equal to:
$
\frac{\text { circumference of circle }}{\text { radius }}=\frac{2 \pi r}{r}=2 \pi
$
- If an angle of $360^{\circ}=2 \pi$ radians, then 1 radian in degrees is equal to:
$
\frac{360}{2 \pi}=\frac{180}{\pi} \simeq 57.30^{\circ}
$
- Use the following equation to convert from degrees to radians:
$
\theta^{\circ} \times\left(\frac{\pi}{180}\right)=\theta \text { rad }
$
Table of common degrees to radians conversions
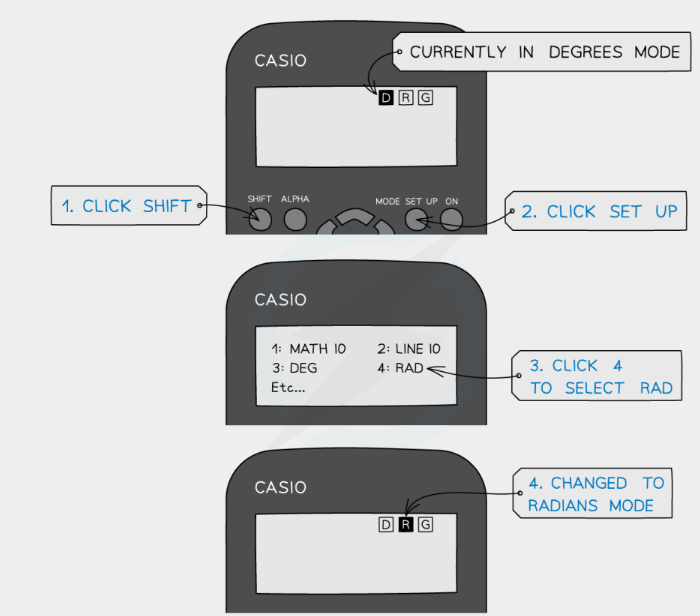
Exam Tip
- You will notice your calculator has a degree (Deg) and radians (Rad) mode
- This is shown by the “D” or ” $R$ ” highlighted at the top of the screen
- Remember to make sure it’s in the right mode when using trigonometric functions (sin, cos, tan) depending on whether the answer is required in degrees or radians
- It is extremely common for students to get the wrong answer (and lose marks) because their calculator is in the wrong mode – make sure this doesn’t happen to you!
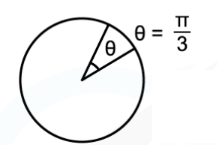
Worked example: Radians conversion
Convert the following angular displacement into degrees
Answer/Explanation
STEP 1 REARRANGE DEGREES TO RADIANS CONVERSION EQUATION
$
\begin{array}{ll}
\text { DEGREES } \rightarrow \text { RADIANS } & \theta^{\circ} \times \frac{\pi}{180}=\theta \text { RAD } \\
\text { RADIANS } \rightarrow \text { DEGREES } & \text { ORAD } \times \frac{180}{\pi}=\theta^{\circ}
\end{array}
$
STEP 2
$
\begin{aligned}
& \text { SUBSTITUTE VALUE } \\
& \qquad \frac{\pi}{3} R A D \times \frac{180}{\pi}=\frac{180^{\circ}}{3}=60^{\circ}
\end{aligned}
$
Angular Speed
- Any object travelling in a uniform circular motion at the same speed travels with a constantly changing velocity
- This is because it is constantly changing direction, and is therefore accelerating
- The angular speed $(\omega)$ of a body in circular motion is defined as:
The rate of change in angular displacement with respect to time
- Angular speed is a scalar quantity, and is measured in rad $\mathrm{s}^{-1}$
When an object is in uniform circular motion, velocity constantly changes direction, but the speed stays the same
Calculating Angular Speed
- Taking the angular displacement of a complete cycle as $2 \pi$, the angular speed $\omega$ can be calculated using the equation:
$
\omega=\frac{\Delta \theta}{\Delta t}=\frac{2 \pi}{T}=2 \pi f
$
- Where:
- $\Delta \theta=$ change in angular displacement (radians)
- $\Delta t=$ time interval (s)
- $T=$ the time period (s)
- $f=$ frequency $(\mathrm{Hz})$
- Angular velocity is the same as angular speed, but it is a vector quantity
- When an object travels at constant linear speed $v$ in a circle of radius $r$, the angular velocity is equal to:
$
\omega=\frac{\Delta \theta}{\Delta t}=\frac{v}{r}
$
- Where:
- $v$ is the linear speed $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- $r$ is the radius of orbit $(\mathrm{m})$
- This equation tells us:
- The greater the rotation angle $\theta$ in a given amount of time, the greater the angular velocity $\omega$
- An object rotating further from the centre of the circle (larger $r$ ) moves with a faster angular velocity (larger $\omega$ )
Worked example: Angular speed
A bird flies in a horizontal circle with an angular speed of 5.25 rads $^{-1}$ of radius $650 \mathrm{~m}$.
Calculate:
a) The linear speed of the bird
b) The frequency of the bird flying in a complete circle
Answer/Explanation
(a)
STEP 1
LINEAR SPEED EQUATION
$
v=r \omega
$
STEP 2
SUBSTITUTE IN VALUES
$
V=650 \times 5.25=3412.5=3410 \mathrm{~ms}^{-1} \quad(3 \text { s.f.) }
$
(b) STEP 1 ANGULAR SPEED WITH FREQUENCY EQUATION
$
\omega=2 \pi f
$
$\begin{aligned} & \text { STEP } 2 \text { REARRANGE FOR FREQUENCY } \\ & f=\frac{\omega}{2 \pi} \\ & \end{aligned}$
STEP 3
SUBSTITUTE IN VALUES
$
f=\frac{5.25}{2 \pi}=0.83556 \ldots=0.836 \mathrm{~Hz}(3 \text { s.f.) }
$
