What Causes Centripetal Acceleration?
- Velocity and acceleration are both vector quantities
- An object in uniform circular motion is continuously changing direction, and therefore is constantly changing velocity
- The object must therefore be accelerating
- This is called the centripetal acceleration and is perpendicular to the direction of the linear speed
- Centripetal means it acts towards the centre of the circular path
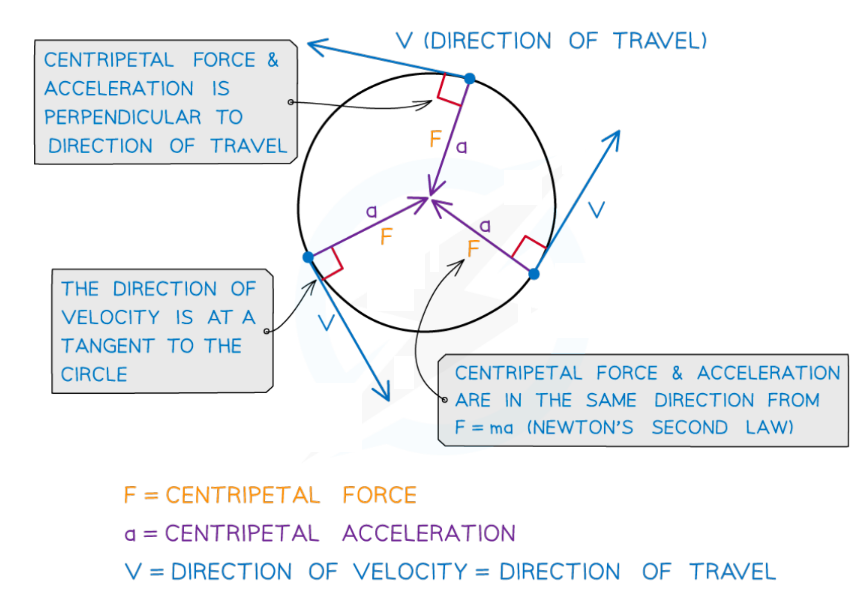
Centripetal force and acceleration are always directed towards the centre of the circle
- The centripetal acceleration is caused by a centripetal force of constant magnitude that also acts perpendicular to the direction of motion (towards the centre)
- Therefore, the centripetal acceleration and force act in the same direction
Exam Tip
- The linear speed is sometimes referred to as the ‘tangential’ speed
- A tangent is a straight line which touches a circle or curve at exactly one point
- The key feature of a tangent of a circle is that it always acts perpendicular to its radius
- You can find out more in the A Level Maths revision notes on Tangents
Relating Centripetal Acceleration & Angular Speed
- An object travelling in uniform circular motion has centripetal acceleration, yet its angular speed $(\omega)$ is constant
- This is because speed is a scalar quantity, whilst velocity is a vector quantity
- Therefore, angular speed is the magnitude (size) component of angular velocity
Key ideas to remember:
- Angular speed (magnitude) stays constant, angular velocity (direction) is constantly changing
- Angular speed does not change with radius, but linear speed does
- The object’s centripetal acceleration is always directed toward the centre of the circle, and is perpendicular to the object’s velocity at any one time
- Velocity and acceleration are both defined by a change in direction, not just a change in the magnitude
Exam Tip
We are used to the idea of acceleration meaning something is speeding up. So, it might sound counterintuitive to say an object travelling in a circle is accelerating, yet it also has constant speed. This is where the idea of scalars and vectors would be useful to revisit if you are not confident with this concept.
12.2.2 CALCULATING CENTRIPETAL ACCELERATION
Calculating Centripetal Acceleration
- Centripetal acceleration can be defined using the radius $r$ and linear speed $v$ :
$
a=\frac{v^2}{r}
$
- Using the equation relating angular speed $\omega$ and linear speed $v$ :
$
\mathbf{v}=\mathbf{r} \boldsymbol{\omega}
$
- These equations can be combined to give us another form of the centripetal acceleration equation:
$
\begin{gathered}
a=\frac{(r \omega)^2}{r} \\
a=r \omega^2
\end{gathered}
$
- This equation tells us centripetal acceleration is equal to the radius times the square of the angular speed
- Alternatively, rearrange for $r$ :
$
r=\frac{v}{\omega}
$
- This equation can be combined with the first one to give us another form of the centripetal acceleration equation:
$
\begin{aligned}
& a=\frac{v^2}{\left(\frac{v}{\omega}\right)} \\
& \mathbf{a}=\mathbf{v} \omega
\end{aligned}
$
- This equation tells us centripetal acceleration is equal to the linear speed times the angular speed
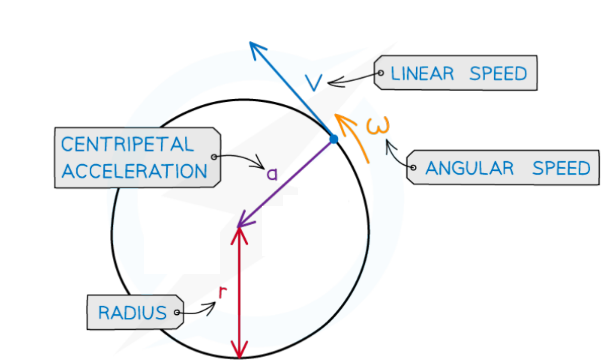
Centripetal acceleration is always directed toward the centre of the circle, and is perpendicular to the object’s velocity
- Where:
- $\mathrm{a}=$ centripetal acceleration $\left(\mathrm{m} \mathrm{s}^{-2}\right)$
- $\mathrm{v}=$ linear speed $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- $\omega=$ angular speed $\left(\mathrm{rad} \mathrm{s}^{-1}\right)$
- $r=$ radius of the orbit $(\mathrm{m})$
Worked example: Centripetal acceleration
A ball tied to a string is rotating in a horizontal circle with radius $1.5 \mathrm{~m}$ and angular speed 3.5 rads $^{-1}$.
Calculate it’s centripetal acceleration with a radius twice as large and angular speed twice as fast.
STEP 1 ANGULAR ACCELERATION EQUATION WITH ANGULAR SPEED
$
a=r \omega^2
$
STEP 2 CHANGE IN ANGULAR ACCELERATION WITH TWICE THE RADIUS AND ANGULAR SPEED
$
a=(2 r) \times(2 \omega)^2=2 r \times 4 \omega^2=8 r \omega^2
$
THE CENTRIPETAL ACCELERATION WILL BE $8 \times$ BIGGER
STEP 3 SUBSTITUTE IN VALUES OF RADIUS AND ANGULAR SPEED
$
a=8 r \omega^2=8 \times 1.5 \times 3.5^2=147 \mathrm{~ms}^{-2}
$
12.2.3 CALCULATING CENTRIPETAL FORCE
Calculating Centripetal Force
- An object moving in a circle is not in equilibrium, it has a resultant force acting upon it
- This is known as the centripetal force and is what keeps the object moving in a circle
- The centripetal force $(F)$ is defined as:
- The resultant perpendicular force towards the centre of the the circle needed to keep a body in uniform circular motion
- Centripetal force can be calculated using:
$
\mathrm{F}=\frac{m v^2}{r}=m r \omega^2=\mathrm{mv} \omega
$
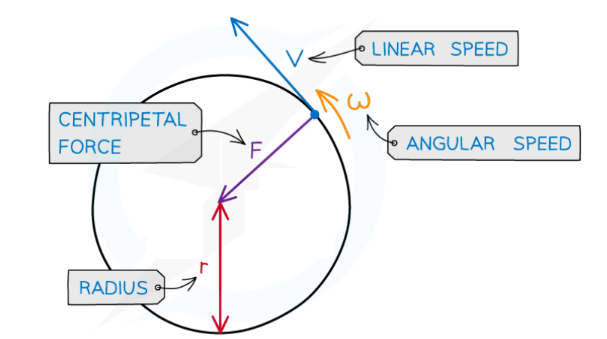
Centripetal force is always perpendicular to the direction of travel
- Where:
- $\mathrm{F}=$ centripetal force $(N)$
- $\mathrm{v}=$ linear velocity $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- $\omega=$ angular speed $\left(\mathrm{rad} \mathrm{s}^{-1}\right)$
- $r=$ radius of the orbit $(\mathrm{m})$
- Note: centripetal force and centripetal acceleration act in the same direction
- This is due to Newton’s Second Law
- The centripetal force is not a separate force of its own
- It can be any type of force, depending on the situation, which keeps an object moving in a circular path
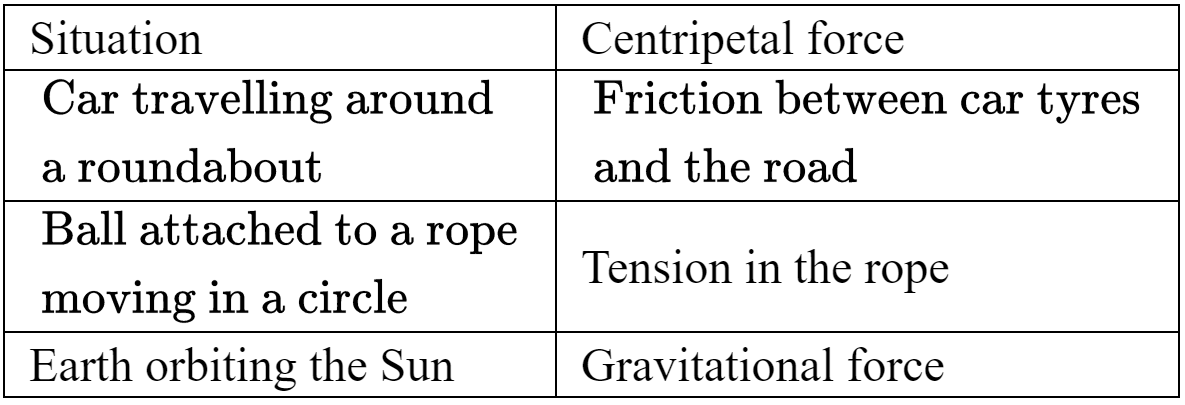
Examples of centripetal force
Worked example: Centripetal force
A bucket of mass $8.0 \mathrm{~kg}$ is filled with water is attached to a string of length $0.5 \mathrm{~m}$ and tension $7.0 \mathrm{~N}$ at the top of the circle.
What is the minimum speed the bucket must have at the top of the circle so no water spills out?
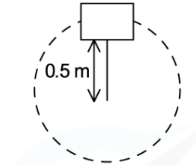
STEP 1 DRAW THE FORCES ON THE BUCKET AT THE TOP
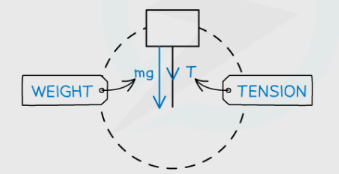
STEP 2 CALCULATE THE CENTRIPETAL FORCE
$
m g+T=\frac{m v^2}{r} \Leftarrow \text { CENTRIPETAL FORCE EQUATION }
$
$\begin{aligned} & \begin{array}{l|l}\text { STEP } 3 & \text { REARRANGE FOR VELOCITY } \vee\end{array} \\ & v=\sqrt{\frac{r(m g+T)}{m}} \\ & \end{aligned}$
STEP 4 SUBSTITUTE IN VALUES
$
\sqrt{\frac{0.5(8.0 \times 9.81+7.0)}{8.0}}=2.31 \mathrm{~ms}^{-1}
$
