Circular Orbits in Gravitational Fields
- Since most planets and satellites have a near circular orbit, the gravitational force $F_G$ between the sun or another planet provides the centripetal force needed to stay in an orbit
- Both the gravitational force and centripetal force are perpendicular to the direction of travel of the planet
- Consider a satellite with mass $m$ orbiting Earth with mass $M$ at a distance $r$ from the centre travelling with linear speed $v$
$
\mathrm{F}_{\mathrm{G}}=\mathrm{F}_{\mathrm{circ}}
$
- Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:
$
\frac{G M m}{r^2}=\frac{m v^2}{r}
$
- The mass of the satellite $m$ will cancel out on both sides to give:
$
\mathrm{v}^2=\frac{G M}{r}
$
- This means that all satellites, whatever their mass, will travel at the same speed $v$ in a particular orbit radius $r$
- Recall that since the direction of a planet orbiting in circular motion is constantly changing, it has centripetal acceleration
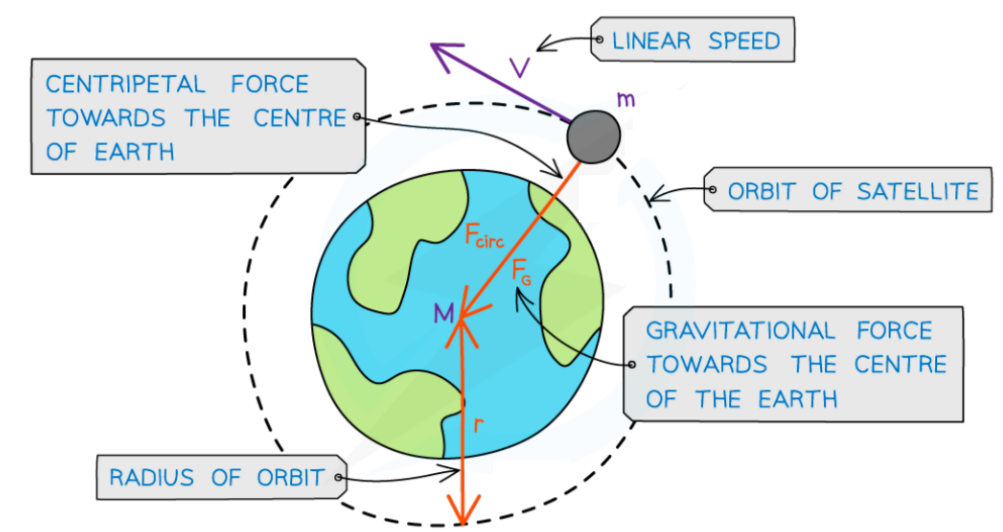
A satellite in orbit around the Earth travels in circular motion
Kepler’s Third Law of Planetary Motion
- For the orbital time period $T$ to travel the circumference of the orbit $2 \pi r$, the linear speed $v$ can be written as
$
v=\frac{2 \pi r}{T}
$
- This is a result of the well-known equation, speed = distance / time
- Substituting the value of the linear speed $v$ into the above equation:
$
v^2=\left(\frac{2 \pi r}{T}\right)^2=\frac{G M}{r}
$
- Rearranging leads to Kepler’s third law equation:
$
\mathrm{T}^2=\frac{4 \pi^2 r^3}{G M}
$
- The equation shows that the orbital period $T$ is related to the radius $r$ of the orbit. This is known as Kepler’s third law:
For planets or satellites in a circular orbit about the same central body, the square of the time period is proportional to the cube of the radius of the orbit - Kepler’s third law can be summarised as:
$
\mathrm{T}^2 \propto \mathrm{r}^3
$
Maths Tip
- The $\propto$ symbol means ‘proportional to’
- Find out more about proportional relationships between two variables in the “proportional relationships ” section of the $A$ Level Maths revision notes
Worked example: Circular orbits in gravitational fields
A binary star system constant of two stars orbiting about a fixed point B.
The star of mass $M_1$ has a circular orbit of radius $R_1$ and mass $M_2$ has a radius of $R_2$. Both have linear speed $v$ and an angular speed $\omega$ about B.
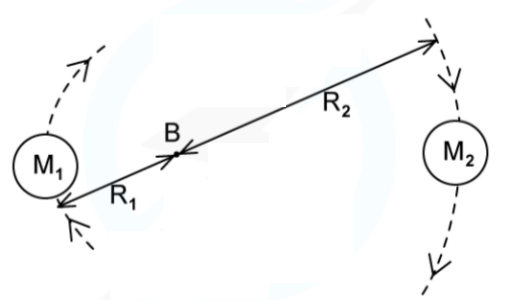
State the following formula, in terms of $G, M_2, R_1$ and $R_2$.
1. The angular speed $\omega$ of $M_1$
2. The time period $\mathbf{T}$ for each star in terms of angular speed $\boldsymbol{\omega}$
(1) The angular speed of $\omega$ of $M_1$
Answer/Explanation
Step 1: Equating the centripetal force of mass $M_1$ to the gravitational force between $M_1$ and $M_2$
$
\mathrm{M}_1 \mathrm{R}_1 \omega^2=\frac{G M_1 M_2}{\left(R_1+R_2\right)^2}
$
Step 2: $\quad M_1$ cancels on both sides
$
\mathrm{R}_1 \omega^2=\frac{G M_2}{\left(R_1+R_2\right)^2}
$
Step 3:
Rearrange for angular velocity $\omega$
$
\omega^2=\frac{G M_2}{R_1\left(R_1+R_2\right)^2}
$
Step 4:
Square root both sides
$
\omega=\sqrt{\frac{G M_2}{R_1\left(R_1+R_2\right)^2}}
$
(2) The time period $\mathrm{T}$ for each star in terms of angular speed $\omega$
Step 1:
Angular speed equation with time period $\mathrm{T}$
$
\omega=\frac{2 \pi}{T}
$
Step 2:
Rearrange for $T$
$
T=\frac{2 \pi}{\omega}
$
Step 3:
Substitute in $\omega$
$
\mathrm{T}=2 \pi \div \sqrt{\frac{G M_2}{R_1\left(R_1+R_2\right)^2}}=2 \pi \sqrt{\frac{R_1\left(R_1+R_2\right)^2}{G M_2}}
$
Exam Tip
Many of the calculations in the Gravitation questions depend on the equations for circular motion. Be sure to revisit these and understand how to use them!
Geostationary Orbits
- Many communication satellites around Earth follow a geostationary orbit
- This is a specific type of orbit in which the satellite:
- Remains directly above the equator, therefore, it always orbits at the same point above the Earth’s surface
- Moves from west to east (same direction as the Earth spins)
- Has an orbital time period equal to Earth’s rotational period of 24 hours
- Geostationary satellites are used for telecommunication transmissions (e.g. radio) and television broadcast
- A base station on Earth sends the TV signal up to the satellite where it is amplified and broadcast back to the ground to the desired locations
- The satellite receiver dishes on the surface must point towards the same point in the sky
- Since the geostationary orbits of the satellites are fixed, the receiver dishes can be fixed too
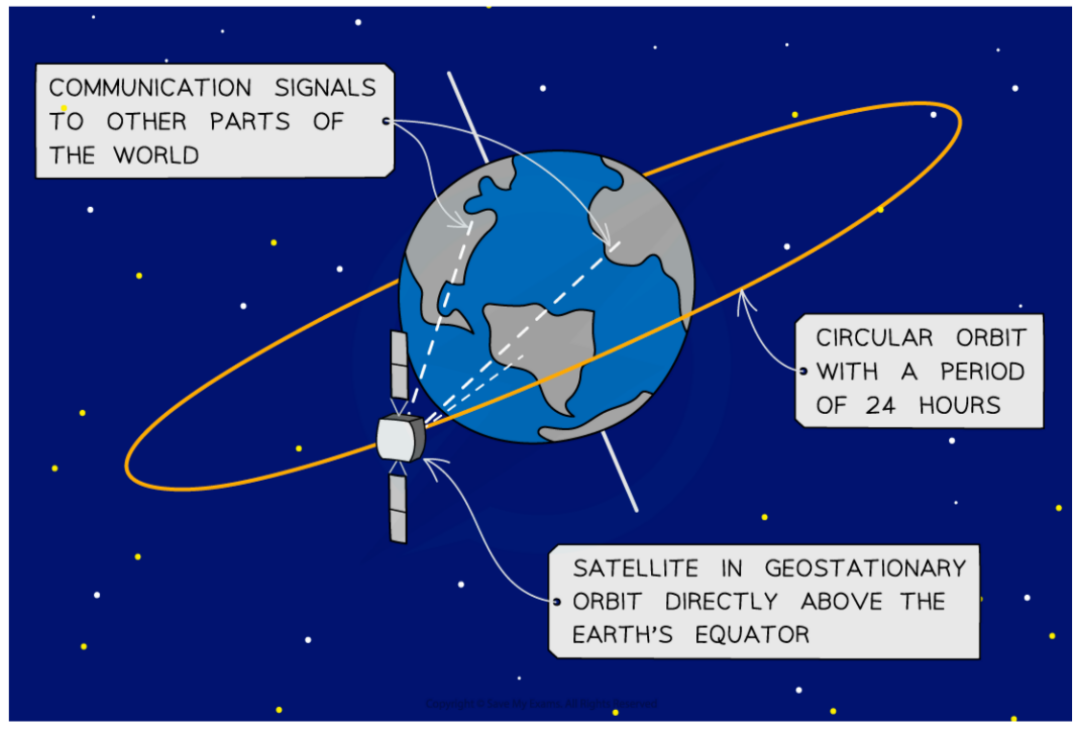
Geostationary satellite in orbit
Worked example: Radius of geostationary orbit
Calculate the distance above the Earth’s surface that a geostationary satellite will orbit Mass of the Earth $=6.0 \times 10^{24} \mathrm{~kg}$. Radius of the Earth $=6400 \mathrm{~km}$.
Answer/Explanation
STEP 1 KEPLER’S THIRD LAW EQUATION
$
T^2=\frac{4 \pi^2 r^3}{G M}
$
STEP 2 REARRANGE FOR $r$, THE RADIUS OF THE ORBIT
$
r=\sqrt[3]{\frac{G M T^2}{4 \pi^2}}
$
STEP 3 SUBSTITUTE IN VALUES
THE TIME PERIOD $T$ FOR A GEOSTATIONARY ORBIT IS 24 HOURS $=86400$ s
$
\begin{aligned}
& r=\sqrt[3]{\frac{6.67 \times 10^{-11} \times 6.0 \times 10^{24} \times(86400)^2}{4 \pi^2}} \\
& r=42297523.87 \mathrm{~m}=4.2 \times 10^7 \mathrm{~m} \text { (2 s.f.) }
\end{aligned}
$
STEP 4 CALCULATE DISTANCE ABOVE THE EARTH’S SURFACE
$r$ IS THE DISTANCE FROM THE CENTRE OF THE EARTH TO THE SATELLITE DISTANCE ABOVE SURFACE $=$ RADIUS OF ORBIT – RADIUS OF EARTH
$=4.2 \times 10^7-6400 \times 10^3$
$=3.6 \times 10^7 \mathrm{~m} \quad$ (2 s.f. $)$
Deriving Gravitational Field Strength $(\mathrm{g})$
- The gravitational field strength at a point describes how strong or weak a gravitational field is at that point
- The gravitational field strength due to a point mass can be derived from combining the equations for Newton’s law of gravitation and gravitational field strength
- For calculations involving gravitational forces, a spherical mass can be treated as a point mass at the centre of the sphere
- Newton’s law of gravitation states that the attractive force $F$ between two masses $M$ and $m$ with separation $r$ is equal to:
$
\mathrm{F}_{\mathrm{G}}=\frac{G M m}{r^2}
$
- The gravitational field strength at a point is defined as the force $F$ per unit mass $m$
$
\mathrm{g}=\frac{F}{m}
$
- Substituting the force $F$ with the gravitational force $F_6$ leads to:
$
g=\frac{F}{m}=\frac{\frac{G M m}{r^2}}{m}
$
- Cancelling mass $m$, the equation becomes:
$
\mathrm{g}=\frac{G M}{r^2}
$
- Where:
- $\mathrm{g}=$ gravitational field strength $\left(\mathrm{N} \mathrm{kg}^{-1}\right)$
- $\mathrm{G}=$ Newton’s Gravitational Constant
- $M=$ mass of the body producing the gravitational field $(\mathrm{kg})$
- $r=$ distance from the mass where you are calculating the field strength (m)
Calculating $g$
- Gravitational field strength, $g$, is a vector quantity
- The direction of $g$ is always towards the centre of the body creating the gravitational field
- This is the same direction as the gravitational field lines
- On the Earth’s surface, $g$ has a constant value of $9.81 \mathrm{~N} \mathrm{~kg}^{-1}$
- However outside the Earth’s surface, $g$ is not constant
- $g$ decreases as $r$ increases by a factor of $1 / r^2$
- This is an inverse square law relationship with distance
- When $g$ is plotted against the distance from the centre of a planet, $r$ has two parts:
- When $r<R$, the radius of the planet, $g$ is directly proportional to $r$
- When $r>R, g$ is inversely proportional to $r^2$ (this is an ‘L’ shaped curve and shows that $g$ decreases rapidly with increasing distance $r$ )
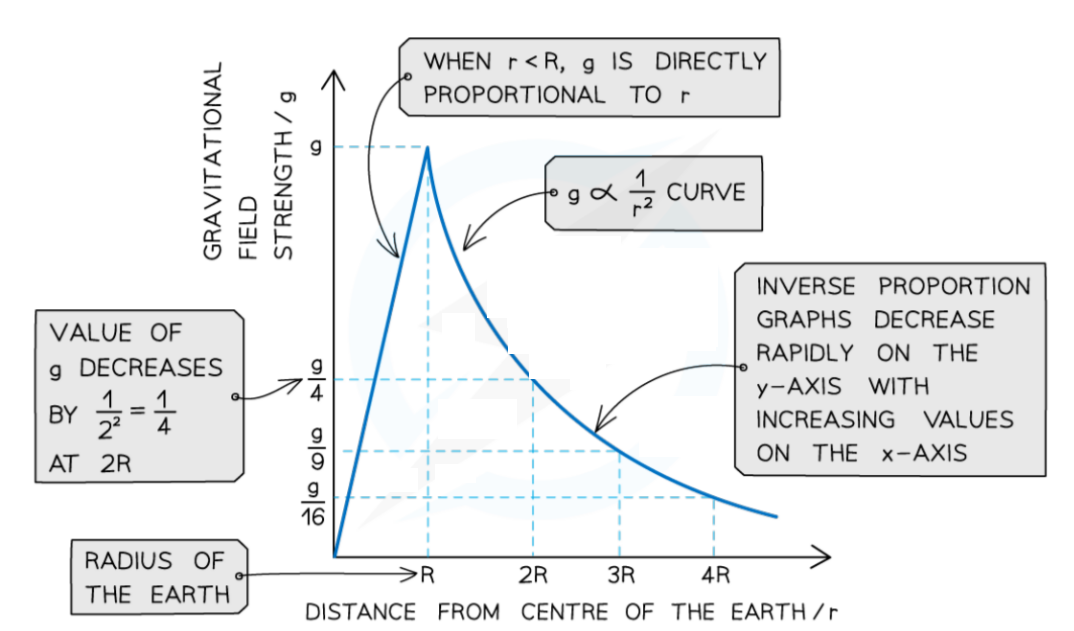
Graph showing how gravitational field strength varies at greater distance from the Earth’s surface
- Sometimes, $g$ is referred to as the ‘acceleration due to gravity’ with units of $\mathrm{m} \mathrm{s}^{-2}$
- Any object that falls freely in a uniform gravitational field on Earth has an acceleration of 9.81 $\mathrm{m} \mathrm{s}^{-2}$
Worked example: Gravitational field strength
The mean density of the Moon is $3 / 5$ times the mean density of the Earth. O The gravitational field strength on the Moon is $1 / 6$ of the value on Earth. Determine the ratio of the Moon’s radius $r_M$ and the Earth’s radius $r_E$.
Answer/Explanation
Step 1: $\quad$ Write down the known quantities
$
\begin{aligned}
& \rho_M=\frac{3}{5} \rho_E \\
& g_M=\frac{1}{6} g_E
\end{aligned}
$
$g_M=$ gravitational field strength on the Moon, $\rho_M=$ mean density of the Moon
$g_{\mathrm{E}}=$ gravitational field strength on the Earth, $\rho_{\mathrm{E}}=$ mean density of the Earth
Step 2:
The volumes of the Earth and Moon are equal to the volume of a sphere
$
V=\frac{4}{3} \pi r^3
$
Step 3:
Write the density equation and rearrange for mass $\mathrm{M}$
$
\begin{aligned}
& \rho=\frac{M}{V} \\
& \mathbf{M}=\rho \mathbf{V}
\end{aligned}
$
Step 4:
Write the gravitational field strength equation
$
g=\frac{G M}{r^2}
$
Step 5: Substitute M in terms of ρ and V
$
g=\frac{G \varrho V}{r^2}
$
Step 6: Substitute the volume of a sphere equation for $V$, and simplify
$
\mathrm{g}=\frac{G 04 \pi r^3}{3 r^2}=\frac{G 04 \pi r}{3}
$
Step 7: Find the ratio of the gravitational field strengths
$
\frac{g_M}{g_E}=\frac{G \varrho_M 4 \pi r_M}{3} \div \frac{G \varrho_E 4 \pi r_E}{3}=\frac{\varrho_M r_M}{\varrho_E r_E}
$
Step 8: Rearrange and calculate the ratio of the Moon’s radius $r_M$ and the Earth’s radius $r_E$
$
\frac{r_M}{r_E}=\frac{\varrho_E g_M}{\varrho_M g_E}=\frac{\varrho_E\left(\frac{1}{6} g_E\right)}{\left(\frac{3}{5} \varrho_E\right) g_E}
$
$
\frac{r_M}{r_E}=\frac{5}{3} \times \frac{1}{6}=\frac{5}{18}=0.28(2 \text { s.f. })
$
- The Value of $g$ on Earth
- Gravitational field strength $g$ is approximately constant for small changes in height near the Earth’s surface $\left(9.81 \mathrm{~m} \mathrm{~s}^{-2}\right)$
- This is because from the inverse square law relationship:
$
g \propto \frac{1}{r^2}
$
- The value of $g$ depends on the distance from the centre of Earth $r$
- On the Earth’s surface, $r$ is equal to the radius of the Earth $=6400 \mathrm{~km}$
- Since this is much larger than the distance between the surface of the earth and centre of mass of an object on it, the small changes in height near the Earth’s surface make very little difference to the value of $g$
- If we take a position $h$ above the Earth’s surface, where it is reasonable to assume $h$ is much smaller than the radius of the Earth $(\mathrm{h}<<\mathrm{R})$ :
$
\mathrm{g}=\frac{G M}{(R+h)^2} \simeq \frac{G M}{(R)^2}
$
- This means $g$ remains approximately constant until a significant distance away from the Earth’s surface
Worked example: g on Mount Everest
- The following worked example proves that g decreases by very little even on the highest point on Earth
The highest point above the Earth’s surface is at the peak of Mount Everest. Given that this is $8800 \mathrm{~m}$ above the Earth’s surface, show that $g$ decreases by $0.6 \%$.
Mass of the Earth $=6.0 \times 10^{24} \mathrm{~kg}$. Radius of the Earth $=6400 \mathrm{~km}$.
Answer/Explanation
STEP 1 GRAVITATIONAL FIELD STRENGTH EQUATION
$
g=\frac{G M}{r^2}
$
STEP 2 DETERMINE THE VALUE OF $r$
$r=$ RADIUS OF THE EARTH + HEIGHT OF MOUNT EVEREST $=6400 \mathrm{~km}+8.800 \mathrm{~km}=6408.8 \mathrm{~km}$
STEP 3 SUBSTITUTE VALUES IN g EQUATION
$
g=\frac{6.67 \times 10^{-11} \times 6.0 \times 10^{24}}{\left(6408.8 \times 10^3\right)^2}=9.746127 \ldots=9.75 \mathrm{~ms}^{-2}(3 \text { s.f. })
$
STEP 4 CALCULATE PERCENTAGE DECREASE
$
\begin{aligned}
& \text { g ON EARTH’S SURFACE }=9.81 \mathrm{~ms}^{-2} \\
& \% \text { DECREASE }=\frac{\text { DECREASE }}{\text { ORIGINAL }} \times 100 \\
& \frac{9.81-9.75}{9.75} \times 100=0.6 \%
\end{aligned}
$
