17.1.1 DESCRIBING OSCILLATIONS
Describing Oscillations
- An oscillation is defined as:
Repeated back and forth movements on either side of any equilibrium position - When the object stops oscillating, it returns to its equilibrium position
- An oscillation is a more specific term for a vibration
- An oscillator is a device that works on the principles of oscillations
- Oscillating systems can be represented by displacement-time graphs similar to transverse waves
- The shape of the graph is a sine curve
- The motion is described as sinusoidal
Properties of Oscillations
- Displacement $(\boldsymbol{x})$ of an oscillating system is defined as:
The distance of an oscillator from its equilibrium position - Amplitude $\left(x_0\right)$ is defined as:
The maximum displacement of an oscillator from its equilibrium position - Angular frequency $(\omega)$ is defined as:
The rate of change of angular displacement with respect to time - This is a scalar quantity measured in $\mathbf{r a d} \mathbf{s}^{-1}$ and is defined by the equation:
$
\omega=\frac{2 \pi}{T}=2 \pi f
$
- Frequency (f) is defined as:
The number of complete oscillations per unit time - It is measured in Hertz $(\mathrm{Hz})$ and is defined by the equation:
$
f=\frac{1}{T}
$
- Time period $(T)$ is defined as:
The time taken for one complete oscillation, in seconds - One complete oscillation is defined as:
The time taken for the oscillator to pass the equilibrium from one side and back again fully from the other side - The time period is defined by the equation:
$
\mathrm{T}=\frac{1}{f}=\frac{2 \pi}{\omega}
$
- Phase difference is how much one oscillator is in front or behind another
- When the relative position of two oscillators are equal, they are in phase
- When one oscillator is exactly half a cycle behind another, they are said to be in antiphase
- Phase difference is normally measured in radians or fractions of a cycle
- When two oscillators are in antiphase they have a phase difference of $\boldsymbol{\pi}$ radians
Worked example: Calculating angular frequency
A student sets out to investigate the oscillation of a mass suspended from the free end of a spring. The mass is pulled downwards and then released. The variation with time $t$ of the displacement $y$ of the mass is shown in the figure below.
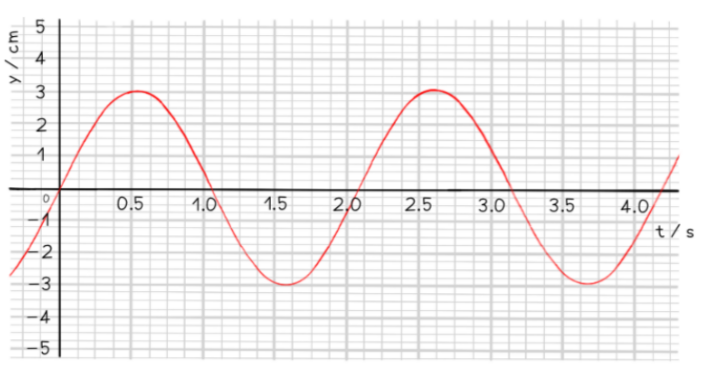
Use the information from the figure to calculate the angular frequency of the oscillations.
▶️Answer/Explanation
Step 1:
Write down the equation for angular frequency
$
\omega=\frac{2 \pi}{T}
$
Step 2:
Calculate the time period $T$ from the graph The time period is defined as the time taken for one complete oscillation This can be read from the graph:
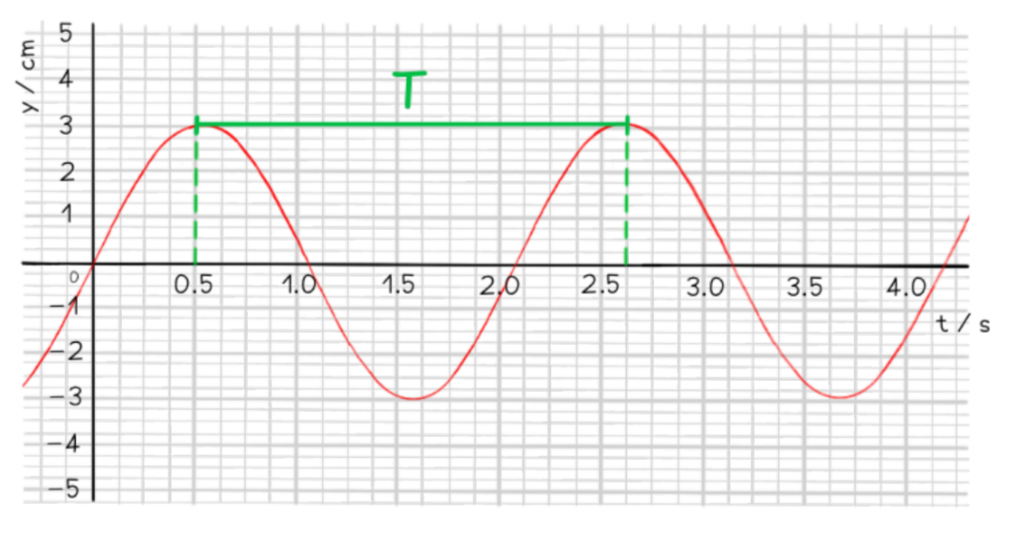
$
T=2.6-0.5=2.1 \mathrm{~s}
$
Step 3:
Substitute into angular frequency equation
$
\omega=\frac{2 \pi}{2.1}=2.9919 \ldots=3.0 \mathrm{rad} \mathrm{s}^{-1}
$
Exam Tip
The properties used to describe oscillations are very similar to transverse waves. The key difference is that oscillators do not have a ‘wavelength’ and their direction of travel is only kept within the oscillations themselves rather than travelling a distance in space.
Conditions for Simple Harmonic Motion
- Simple harmonic motion (SHM) is a specific type of oscillation
- SHM is defined as:
A type of oscillation in which the acceleration of a body is proportional to its displacement, but acts in the opposite direction - Examples of oscillators that undergo SHM are:
- The pendulum of a clock
- A mass on a spring
- Guitar strings
- The electrons in alternating current flowing through a wire
- This means for an object to oscillate specifically in SHM, it must satisfy the following conditions:
- Periodic oscillations
- Acceleration proportional to its displacement
- Acceleration in the opposite direction to its displacement
- Acceleration $a$ and displacement $x$ can be represented by the defining equation of SHM:
$
a \propto-x
$
- An object in SHM will also have a restoring force to return it to its equilibrium position
- This restoring force will be directly proportional, but in the opposite direction, to the displacement of the object from the equilibrium position
- Note: the restoring force and acceleration act in the same direction
- This is why a person jumping on a trampoline is not an example of simple harmonic motion:
- The restoring force on the person is not proportional to their distance from the equilibrium position
- When the person is not in contact with the trampoline, the restoring force is equal to their weight, which is constant
- This does not change, even if they jump higher
Calculating Acceleration & Displacement of an Oscillator
- The acceleration of an object oscillating in simple harmonic motion is:
$
\mathbf{a}=-\omega^2 \mathbf{x}
$
- Where:
$
\begin{aligned}
& \circ \mathrm{a}=\text { acceleration }\left(\mathrm{m} \mathrm{s}^{-2}\right) \\
& \circ \omega=\text { angular frequency }\left(\mathrm{rad} \mathrm{s}^{-1}\right) \\
& \circ \mathrm{x}=\text { displacement }(\mathrm{m})
\end{aligned}
$
- This is used to find the acceleration of an object in SHM with a particular angular frequency $\omega$ at a specific displacement $x$
- The equation demonstrates:
- The acceleration reaches its maximum value when the displacement is at a maximum ie. $x=x_0$ (amplitude)
- The minus sign shows that when the object is displacement to the right, the direction of the acceleration is to the left
- The graph of acceleration against displacement is a straight line through the origin sloping downwards (similar to $y=-x$ )
- Key features of the graph:
- The gradient is equal to $-\omega^2$
- The maximum and minimum displacement $x$ values are the amplitudes $-x_0$ and $+x_0$
- A solution to the SHM acceleration equation is the displacement equation:
$
x=x_0 \sin (\omega t)
$
- Where:
$
\begin{aligned}
& \circ \mathrm{x}=\text { displacement }(\mathrm{m}) \\
& \circ \mathrm{x}_0=\text { amplitude }(\mathrm{m}) \\
& \circ \mathrm{t}=\text { time (s) }
\end{aligned}
$
- This equation can be used to find the position of an object in SHM with a particular angular frequency and amplitude at a moment in time
- Note: This version of the equation is only relevant when an object begins oscillating from the equilibrium position $(x=0$ at $t=0)$
- The displacement will be at its maximum when $\sin (\omega t)$ equals 1 or -1 , when $\mathrm{x}=\mathrm{x}_0$
- If an object is oscillating from its amplitude position $\left(x=x_0\right.$ or $x=-x_0$ at $t=0$ ) then the displacement equation will be:
$
x=x_0 \cos (\omega t)
$
- This is because the cosine graph starts at a maximum, whilst the sine graph starts at 0
Worked example: Calculating SHM displacement
A mass of $55 \mathrm{~g}$ is suspended from a fixed point by means of a spring. The stationary mass is pulled vertically downwards through a distance of $4.3 \mathrm{~cm}$ and then released at $t=0$. The mass is observed to perform simple harmonic motion with a period of $0.8 \mathrm{~s}$. Calculate the displacement $x$, in $\mathrm{cm}$, of the mass at time $t=0.3 \mathrm{~s}$.
▶️Answer/Explanation
Step 1:
Write down the SHM displacement equation
Since the mass is released at $\mathrm{t}=0$ at its maximum displacement, the displacement equation will be with the cosine function:
$
x=x_0 \cos (\omega t)
$
Step 2:
Calculate angular frequency
$
\omega=\frac{2 \pi}{T}=\frac{2 \pi}{0.8}=7.85 \mathrm{rads}^{-1}
$
Remember to use the value of the time period given, not the time where you are calculating the displacement from
Step 3:
Substitute values into the displacement equation
$
x=4.3 \cos (7.85 \times 0.3)=-3.0369 \ldots=-3.0 \mathrm{~cm}(2 \mathrm{s.f})
$
Make sure the calculator is in radians mode The negative value means the mass is $3.0 \mathrm{~cm}$ on the opposite side of the equilibrium position to where it started $(3.0 \mathrm{~cm}$ above it)
Exam Tip
Since displacement is a vector quantity, remember to keep the minus sign in your solutions if they are negative, you could lose a mark if not! Also remember that your calculator must be in radians mode when using the $\cos$ and sine functions. This is because the angular frequency $\omega$ is calculated in rad $\mathrm{s}^{-1}$, not degrees.
Calculating Speed of an Oscillator
- The speed of an object in simple harmonic motion varies as it oscillates back and forth – Its speed is the magnitude of its velocity
- The greatest speed of an oscillator is at the equilibrium position ie. when its displacement is $0(x=0)$
- The speed of an oscillator in SHM is defined by:
$
v=v_0 \cos (\omega t)
$
- Where:
$
\begin{aligned}
& \circ \mathrm{v}=\text { speed }\left(\mathrm{m} \mathrm{s}^{-1}\right) \\
& \circ \mathrm{v}_0=\text { maximum speed }\left(\mathrm{m} \mathrm{s}^{-1}\right) \\
& \circ \mathrm{\omega}=\text { angular frequency }\left(\mathrm{rad} \mathrm{s}^{-1}\right) \\
& \circ \mathrm{t}=\text { time }(\mathrm{s})
\end{aligned}
$
- This is a cosine function if the object starts oscillating from the equilibrium position $(x=0$ when $t=0$ )
- Although the symbol $v$ is commonly used to represent velocity, not speed, exam questions focus more on the magnitude of the velocity than its direction in SHM
- How the speed $v$ changes with the oscillator’s displacement $x$ is defined by:
$
\mathrm{v}= \pm \omega \sqrt{\left(x_0^2-x^2\right)}
$
- Where:
- $x=$ displacement $(\mathrm{m})$
- $x_0=$ amplitude $(\mathrm{m})$
- $\circ \pm=$ ‘plus or minus’. The value can be negative or positive
- This equation show that when an oscillator has a greater amplitude $x_0$, it has to travel a greater distance in the same time and hence has greater speed $v$
- Both equations for speed will be given on your formulae sheet in the exam
- When the speed is at its maximums (at $x=0$ ), the equation becomes:
$
\mathbf{v}_0=\boldsymbol{\omega} \mathrm{x}_0
$
Worked example: Calculating the speed of a pendulum
A simple pendulum oscillates with simple harmonic motion with an amplitude of $15 \mathrm{~cm}$. The frequency of the oscillations is $6.7 \mathrm{~Hz}$. Calculate the speed of the pendulum at a position of $12 \mathrm{~cm}$ from the equilibrium position.
▶️Answer/Explanation
Step 1:
Write out the known quantities
Amplitude of oscillations, $x_0=15 \mathrm{~cm}=0.15 \mathrm{~m}$
Displacement at which the speed is to be found, $\mathbf{x}=12 \mathbf{c m}=\mathbf{0 . 1 2} \mathbf{m}$
Frequency, $\mathbf{f}=\mathbf{6 . 7} \mathrm{Hz}$
Step 2:
Oscillator speed with displacement equation
$
v= \pm \omega \sqrt{\left(x_0^2-x^2\right)}
$
Since the speed is being calculated, the \pm sign can be removed as direction does not matter in this case
Step 3:
Write an expression for the angular frequency
Equation relating angular frequency and normal frequency:
$
\omega=2 \pi f=2 \pi \times 6.7=42.097 \ldots
$
Step 4:
Substitute in values and calculate
$
v=(2 \pi \times 6.7) \times \sqrt{(0.15)^2-(0.12)^2}
$
$
v=3.789=3.8 \mathrm{~m} \mathrm{~s}^{-1}(2 \mathrm{s.f})
$
Exam Tip
You often have to convert between time period $T$, frequency $f$ and angular frequency $\omega$ for many exam questions – so make sure you revise the equations relating to these.
SHM Graphs
- The displacement, velocity and acceleration of an object in simple harmonic motion can be represented by graphs against time
- All undamped SHM graphs are represented by periodic functions
- This means they can all be described by sine and cosine curves
Key features of the displacement-time graph:
- The amplitude of oscillations $x_0$ can be found from the maximum value of $x$
- The time period of oscillations $T$ can be found from reading the time taken for one full cycle
- The graph might not always start at 0
- If the oscillations starts at the positive or negative amplitude, the displacement will be at its maximum
Key features of the velocity-time graph:
- It is $90^{\circ}$ out of phase with the displacement-time graph
- Velocity is equal to the rate of change of displacement
- So, the velocity of an oscillator at any time can be determined from the gradient of the displacement-time graph:
$
\mathrm{v}=\frac{\Delta x}{\Delta t}
$
- An oscillator moves the fastest at its equilibrium position
- Therefore, the velocity is at its maximum when the displacement is zero
- Key features of the acceleration-time graph:
- The acceleration graph is a reflection of the displacement graph on the $x$ axis
- This means when a mass has positive displacement (to the right) the acceleration is in the opposite direction (to the left) and vice versa
- It is $90^{\circ}$ out of phase with the velocity-time graph
- Acceleration is equal to the rate of change of velocity
- So, the acceleration of an oscillator at any time can be determined from the gradient of the velocity-time graph:
$
\mathrm{a}=\frac{\Delta v}{\Delta t}
$
- The maximum value of the acceleration is when the oscillator is at its maximum displacement
Worked example: Using SHM graph data
A swing is pulled $5 \mathrm{~cm}$ and then released. The variation of the horizontal displacement $x$ of the swing with time $t$ is shown on the graph below.
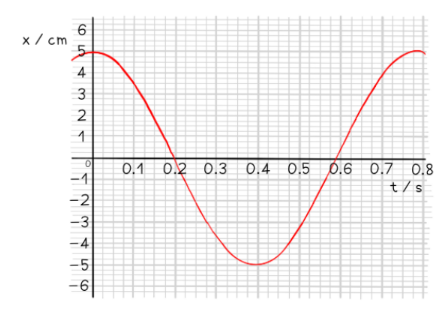
The swing exhibits simple harmonic motion. Use data from the graph to determine at what time the velocity of the swing is first at its maximum.
▶️Answer/Explanation
Step 1: The velocity is at its maximum when the displacement $x=0$
Step 2: $\quad$ Reading value of time when $x=0$
From the graph this is equal to $0.2 \mathrm{~s}$
Exam Tip
These graphs might not look identical to what is in your textbook, depending on where the object starts oscillating from at $t=0$ (on either side of the equilibrium, or at the equilibrium). However, if there is no damping, they will all always be a general sine or cosine curves.
