Kinetic & Potential Energies
- During simple harmonic motion, energy is constantly exchanged between two forms: kinetic and potential
- The potential energy could be in the form of:
- Gravitational potential energy (for a pendulum)
- Elastic potential energy (for a horizontal mass on a spring)
- Or both (for a vertical mass on a spring)
- Speed $v$ is at a maximum when displacement $\mathrm{x}=0$, so:
The kinetic energy is at a maximum when the displacement $x=0$ (equilibrium position) - Therefore, the kinetic energy is 0 at maximum displacement $x=x_0$, so:
The potential energy is at a maximum when the displacement (both positive and negative) is at a maximum $x=x_0$ (amplitude) - A simple harmonic system is therefore constantly converting between kinetic and potential energy
- When one increases, the other decreases and vice versa, therefore:
The total energy of a simple harmonic system always remains constant and is equal to the sum of the kinetic and potential energies
- The key features of the energy-time graph:
- Both the kinetic and potential energies are represented by periodic functions (sine or cosine) which are varying in opposite directions to one another
- When the potential energy is 0 , the kinetic energy is at its maximum point and vice versa
- The total energy is represented by a horizontal straight line directly above the curves at the maximum value of both the kinetic or potential energy
- Energy is always positive so there are no negative values on the $y$ axis
- Note: kinetic and potential energy go through two complete cycles during one period of oscillation
- This is because one complete oscillation reaches the maximum displacement twice (positive and negative)
The key features of the energy-displacement graph:
- Displacement is a vector, so, the graph has both positive and negative $x$ values
- The potential energy is always at a maximum at the amplitude positions $x_0$ and 0 at the equilibrium position $(x=0)$
- This is represented by a ‘ $U$ ‘ shaped curve
- The kinetic energy is the opposite: it is 0 at the amplitude positions $x_0$ and maximum at the equilibrium position $x=0$
- This is represented by a ‘ $n$ ‘ shaped curve
- The total energy is represented by a horizontal straight line above the curves
Exam Tip
You may be expected to draw as well as interpret energy graphs against time or displacement in exam questions. Make sure the sketches of the curves are as even as possible and use a ruler to draw straight lines, for example, to represent the total energy.
Calculating Total Energy of a Simple Harmonic System
- The total energy of system undergoing simple harmonic motion is defined by:
$
E=\frac{1}{2} m \omega^2 x_0^2
$
- Where:
- $\circ \mathrm{E}=$ total energy of a simple harmonic system $(\mathrm{J})$
- $\circ \mathrm{m}=$ mass of the oscillator $(\mathrm{kg})$
- $\circ \mathrm{\omega}=$ angular frequency $\left(\mathrm{rad} \mathrm{s}^{-1}\right)$
- $\circ \mathrm{x}_0=$ amplitude $(\mathrm{m})$
Worked example: Calculating the total energy of oscillations
A ball of mass $23 \mathrm{~g}$ is held between two fixed points $\mathrm{A}$ and $B$ by two stretch helical springs, as shown in the diagram below.
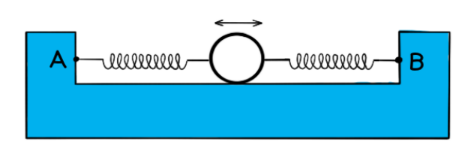
The ball oscillates with simple harmonic motion along the line $A B$ with frequency $4.8 \mathrm{~Hz}$ and amplitude $1.5 \mathrm{~cm}$.
Calculate the total energy of the oscillations.
▶️Answer/Explanation
Step 1:
Write down all known quantities
$
\text { Mass, } \mathrm{m}=23 \mathrm{~g}=23 \times 10^{-3} \mathrm{~kg}
$
Amplitude, $\mathrm{x}_0=1.5 \mathrm{~cm}=\mathbf{0 . 0 1 5} \mathbf{~ m}$
Frequency, $f=4.8 \mathrm{~Hz}$
Step 2:
Write down the equation for the total energy of SHM oscillations:
$
E=\frac{1}{2} m \omega^2 x_0^2
$
Step 3:
Write an expression for the angular frequency
$
\omega=2 \pi f=2 \pi \times(4.8)
$
Step 4:
Substitute values into energy equation
$
E=\frac{1}{2} \times\left(23 \times 10^{-3}\right) \times(2 \pi \times 4.8)^2 \times(0.015)^2
$
$
E=2.354 \times 10^{-3}=2.4 \mathrm{~mJ}(2 \mathrm{s.f})
$
