RECTIFICATION
Rectification Graphs
– Rectification is defined as:
The process of converting alternating current and voltage into direct current and voltage
– Rectification is used in electronic equipment which requires a direct current
– For example, mains voltage must be rectified from the alternating voltage produced at power stations
– There are two types of rectification:
– Half-wave rectification
– Full-wave rectification
– For half-wave rectification:
– The graph of the output voltage $V_{\text {out }}$ against time is a sine curve with the positive cycles and a flat line $\left(V_{\text {out }}=0\right)$ on the negative cycle
– This is because the diode only conducts in the positive direction
– For full-wave rectification:
– The graph of the output voltage $V_{\text {out }}$ against time is a sine curve where the positive cycles and the negative cycles are both curved ‘bumps’
Half-Wave Rectification
– Half-wave rectification consists of a single diode
– An alternating input voltage is connected to a circuit with a load resistor and diode in series
– The diode will only conduct during the positive cycles of the input alternating voltage, – Hence there is only current in the load resistor during these positive cycles
– The output voltage $V_{\text {out }}$ across the resistor will fluctuate against against time in the same way as the input alternating voltage except there are no negative cycles
– This type of rectification means half of the time the voltage is zero
– So, the power available from a half-wave rectified supply is reduced
Full-Wave Rectification
- Full-wave rectification requires a bridge rectifier circuit
- This consists of four diodes connected across an input alternating voltage supply
- The output voltage $V_{\text {out }}$ is taken across a load resistor
- During the positive cycles of the input voltage, one terminal if the voltage supply is positive and the other negative
- Two diodes opposite each other that are in forward bias will conduct
- The other two in reverse bias will not conduct
- A current will flow in the load resistor with the positive terminal at the top of the resistor
- During the negative cycles of the input voltage, the positive and negative terminals of the input alternating voltage supply will swap
- The two diodes that were forward bias will now be in reverse bias and not conduct
- The other two in reverse bias will now be in forward bias and will conduct
- The current in the load resistor will still flow in the same direction as before
- In both the positive and negative cycles, the current in the load resistor is the same
- Each diode pair is the same as in half-wave rectification
- Since there are two pairs, this equates to full-wave rectification overall
- The main advantage of full-wave rectification compared to half-wave rectification is that there is more power available
- Therefore, a greater power is supplied on every half cycle
Worked example
(2) A bridge rectifier consists of four ideal diodes A, B, C and D, as connected in the figure shown below.
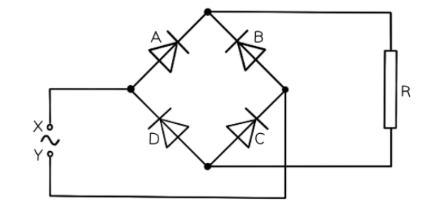
An alternating supply is applied between the terminal $\mathrm{X}$ and $\mathrm{Y}$.
State which diodes are conducting when terminal $X$ of the supply is positive.
Answer/Explanation
- Draw path of the current direction with diodes in forward bias
- Remember that conventional current flow is from positive to negative and only travels through the paths with diodes in forward bias
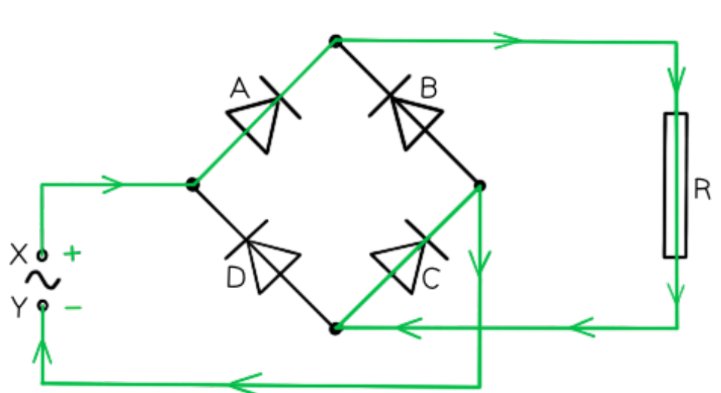
Therefore, the answer is: diodes A and C
Smoothing
- In rectification, to produce a steady direct current or voltage from an alternating current or voltage, a smoothing capacitor is necessary
- Smoothing is defined as:
The reduction in the variation of the output voltage or current - This works in the following ways:
- A single capacitor with capacitance $\mathrm{C}$ is connected in parallel with a load resistor of resistance $R$
- The capacitor charges up from the input voltage and maintains the voltage at a high level
- As it discharges gradually through the resistor when the rectified voltage drops but the voltage then rises again and the capacitor charges up again
- The resulting graph of a smoothed output voltage $V_{\text {out }}$ and output current against time is a ‘ripple’ shape
- The amount of smoothing is controlled by the capacitance $C$ of the capacitor and the resistance $R$ of the load resistor
- The less the rippling effect, the smoother the rectified current and voltage output
- The slower the capacitor discharges, the more the smoothing that occurs ie. smaller ripples
- This can be achieved by using:
- A capacitor with greater capacitance $C$
- A resistance with larger resistor $R$
- Recall that the product $\mathrm{RC}$ is the time constant $\tau$ of a resistor
- This means that the time constant of the capacitor must be greater than the time interval between the adjacent peaks of the output signal
Worked example
The graph below shows the output voltage from a half-wave rectifier. The load resistor has a resistance of $2.6 \mathrm{k} \Omega$. A student wishes to smooth the output voltage by placing a capacitor in parallel across the load resistor.
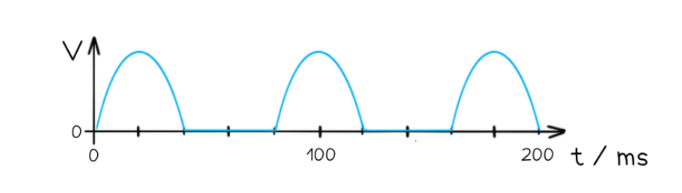
Using an appropriate calculation, suggest if a capacitor of $60 \mathrm{pF}$ or $800 \mu \mathrm{F}$ would be suitable for this task.
Answer/Explanation
Step 1:
Calculate the time constant with the $60 \mathrm{pF}$ capacitor
$
\tau=R C=\left(2.6 \times 10^3\right) \times\left(60 \times 10^{-12}\right)=1.56 \times 10^{-7} \mathrm{~s}=156 \mathrm{~ns}
$
Step 2:
- Compare time constant of $60 \mathrm{pF}$ capacitor with interval between adjacent peaks of the output signal
- The time interval between adjacent peaks is $80 \mathrm{~ms}$
- The time constant of $156 \mathrm{~ns}$ is too small and the $60 \mathrm{pF}$ capacitor will discharge far too quickly
- There would be no smoothing of the output voltages
- Therefore, the $60 \mathrm{pF}$ capacitor is not suitable
Step 3:
- Calculate the time constant with the $800 \mu \mathrm{F}$ capacitor
$
\tau=R C=\left(2.6 \times 10^3\right) \times\left(800 \times 10^{-6}\right)=2.08 \mathrm{~s}
$
Step 4:
Compare time constant of $60 \mathrm{pF}$ capacitor with interval between adjacent peaks of the output signal
- The time constant of $2.08 \mathrm{~s}$ is much larger than $80 \mathrm{~ms}$
- The capacitor will not discharge completely between the positive cycles of the halfwave rectified signal
- Therefore, the $\mathbf{8 0 0} \boldsymbol{\mu} \mathrm{F}$ capacitor would be suitable for the smoothing task
