The Photoelectric Effect: Basics
- The photoelectric effect is the phenomena in which electrons are emitted from the surface of a metal upon the absorption of electromagnetic radiation
- Electrons removed from a metal in this manner are known as photoelectrons
- The photoelectric effect provides important evidence that light is quantised, or carried in discrete packets
- This is shown by the fact each electron can absorb only a single photon
- This means only the frequencies of light above a threshold frequency will emit a photoelectron
- Observing the Photoelectric Effect
- The photoelectric effect can be observed on a gold leaf electroscope
- A plate of metal, usually zinc, is attached to a gold leaf, which initially has a negative charge, causing it to be repelled by a central negatively charged rod
- This causes negative charge, or electrons, to build up on the zinc plate
- UV light is shone onto the metal plate, leading to the emission of photoelectrons
- This causes the extra electrons on the central rod and gold leaf to be removed, so, the gold leaf begins to fall back towards the central rod
- This is because they become less negatively charged, and hence repel less
- Some notable observations:
- Placing the UV light source closer to the metal plate causes the gold leaf to fall more quickly
- Using a higher frequency light source does not change the how quickly the gold leaf falls
- Using a filament light source causes no change in the gold leaf’s position
- Using a positively charged plate also causes no change in the gold leaf’s positionLorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
THRESHOLD FREQUENCY
Threshold Frequency & Wavelength
- The concept of a threshold frequency is required in order to explain why a low frequency source, such as a filament lamp, was unable to liberate any electrons in the gold leaf experiment
- The threshold frequency is defined as:
The minimum frequency of incident electromagnetic radiation required to remove a photoelectron from the surface of a metal - The threshold wavelength, related to threshold frequency by the wave equation, is defined as:
The longest wavelength of incident electromagnetic radiation that would remove a photoelectron from the surface of a metal
- Threshold frequency and wavelength are properties of a material, and vary from metal to metal
Exam Tip
A useful analogy for threshold frequency is a fairground coconut shy:
- One person is throwing table tennis balls at the coconuts, and another person has a pistol
- No matter how many of the table tennis balls are thrown at the coconut it will still stay firmly in place – this represents the low frequency quanta
- However, a single shot from the pistol will knock off the coconut immediately – this represents the high frequency quanta
The Photoelectric Equation
- Since energy is always conserved, the energy of an incident photon is equal to:
The threshold energy + the kinetic energy of the photoelectron - The energy within a photon is equal to $\boldsymbol{h f}$
- This energy is transferred to the electron to release it from a material (the work function) and gives the emitted photoelectron the remaining amount as kinetic energy
- This equation is known as the photoelectric equation:
$
\boldsymbol{E}=\boldsymbol{h f}=\boldsymbol{\phi}+1 / 2 m v_{\text {max }}^2
$
- Symbols:
- $\mathrm{h}=$ Planck’s constant $(\mathrm{J}$ s)
- $f=$ the frequency of the incident radiation $(\mathrm{Hz})$
- $\Phi=$ the work function of the material (J)
- $1 / 2 m v_{\max }^2=$ the maximum kinetic energy of the photoelectrons (J)
- This equation demonstrates:
- If the incident photons do not have a high enough frequency (f) and energy to overcome the work function $(\Phi)$, then no electrons will be emitted
- When $\mathrm{hf}_0=\Phi$, where $\mathrm{f}_0=$ threshold frequency, photoelectric emission only just occurs
- $E_{\text {kmax }}$ depends only on the frequency of the incident photon, and not the intensity of the radiation
- The majority of photoelectrons will have kinetic energies less than $\mathrm{E}_{\mathrm{kmax}}$
Graphical Representation of Work Function
- The photoelectric equation can be rearranged into the straight line equation:
- $
y=m x+c
$ - Comparing this to the photoelectric equation:
$
E_{k \max }=h f-\Phi
$
- A graph of maximum kinetic energy $E_{\text {kmax }}$ against frequency $f$ can be obtained
- The key elements of the graph:
- The work function $\Phi$ is the $y$-intercept
- The threshold frequency $f_0$ is the $x$-intercept
- The gradient is equal to Planck’s constant $h$
- There are no electrons emitted below the threshold frequency $f_0$
Worked example: Calculating work function
The graph below shows how the maximum kinetic energy $E_k$ of electrons emitted from the surface of sodium metal varies with the frequency $f$ of the incident radiation.
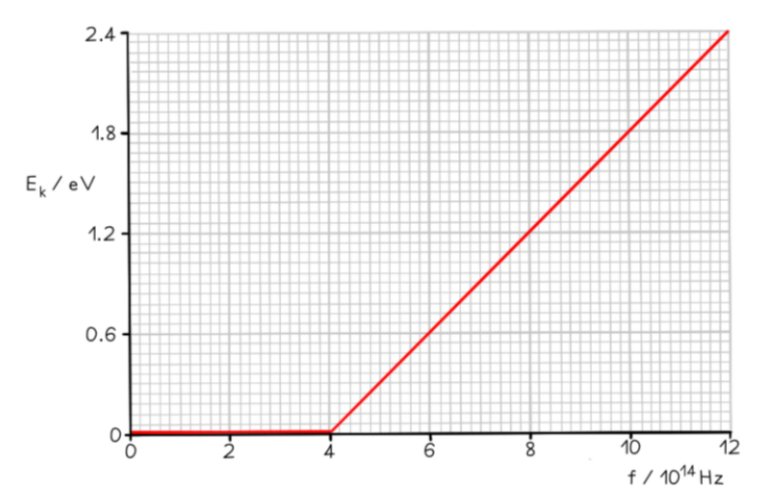
Calculate the work function of sodium in $\mathrm{eV}$.
Step 1: Write out the photoelectric equation and rearrange to fit the equation of a straight line
$
\begin{gathered}
E=h f=\Phi+1 / 2 m v_{\text {max }}^2 \rightarrow E_{\text {kmax }}=\boldsymbol{h f}-\boldsymbol{\Phi} \\
y=\boldsymbol{m x}+\boldsymbol{c}
\end{gathered}
$
Step 2: Identify the threshold frequency from the $x$-axis of the graph
$
\text { When } E_k=0, f=f_0
$
Therefore, the threshold frequency is $f_0=4 \times 10^{14} \mathrm{~Hz}$
Step 3:
Calculate the work function
From the graph at $f_0, 1 / 2 \mathrm{mv}_{\max }{ }^2=0$
$
\Phi=h f_0=\left(6.63 \times 10^{-34}\right) \times\left(4 \times 10^{14}\right)=2.652 \times 10^{-19} \mathrm{~J}
$
Step 4: Convert the work function into $\mathrm{eV}$
$
1 \mathrm{eV}=1.6 \times 10^{-19} \mathrm{~J} \quad \mathrm{~J} \rightarrow \mathrm{eV}: \text { divide by } 1.6 \times 10^{-19}
$
$
E=\frac{2.652 \times 10^{-19}}{1.6 \times 10^{-19}}=1.66 \mathrm{eV}
$
Photoelectric Emission
- The work function $\Phi$, or threshold energy, of a material is defined as:
The minimum energy required to release a photo electron from the surface of a material - Consider the electrons in a metal as trapped inside an ‘energy well’ where the energy between the surface and the top of the well is equal to the work function $\Phi$
- A single electron absorbs one photon
- Therefore, an electron can only escape the surface of the metal if it absorbs a photon which has an energy equal to $\Phi$ or higher
- Different metals have different threshold frequencies, and hence different work functions
- Using the well analogy:
- A more tightly bound electron requires more energy to reach the top of the well
- A less tightly bound electron requires less energy to reach the top of the well
- Alkali metals, such as sodium and potassium, have threshold frequencies in the visible light region
- This is because the attractive forces between the surface electrons and positive metal ions are relatively weak
- Transition metals, such as zinc and iron, have threshold frequencies in the ultraviolet region
- This is because the attractive forces between the surface electrons and positive metal ions are much stronger
Laws of Photoelectric Emission
- Observation:
- Placing the UV light source closer to the metal plate causes the gold leaf to fall more quickly
- Explanation:
- Placing the UV source closer to the plate increases the intensity incident on the surface of the metal
- Increasing the intensity, or brightness, of the incident radiation increases the number of photoelectrons emitted per second
- Therefore, the gold leaf loses negative charge more rapidly
- Observation:
- Using a higher frequency light source does not change the how quickly the gold leaf falls
- Explanation:
- The maximum kinetic energy of the emitted electrons increases with the frequency of the incident radiation
- In the case of the photoelectric effect, energy and frequency are independent of the intensity of the radiation
- So, the intensity of the incident radiation affects how quickly the gold leaf falls, not the frequency
- – Observation:
– Using a filament light source causes no change in the gold leaf’s position
– Explanation:
– If the incident frequency is below a certain threshold frequency, no electrons are emitted, no matter the intensity of the radiation
– A filament light source has a frequency below the threshold frequency of the metal, so, no photoelectrons are released
– Observation:
– Using a positively charged plate causes no change in the gold leaf’s position
– Explanation:
– If the plate is positively charged, that means there is an excess of positive charge on the surface of the metal plate
– Electrons are negatively charged, so they will not be emitted unless they are on the surface of the metal
– Any electrons emitted will be attracted back by positive charges on the surface of the metal - – Observation:
– Emission of photoelectrons happens as soon as the radiation is incident on the surface of the metal
– Explanation:
– A single photon interacts with a single electron
– If the energy of the photon is equal to the work function of the metal, photoelectrons will be released instantaneously
Intensity \& Photoelectric Current
– The maximum kinetic energy of the photoelectrons is independent of the intensity of the incident radiation
– This is because each electron can only absorb one photon
– Kinetic energy is only dependent on the frequency of the incident radiation
– Intensity is a measure of the number of photons incident on the surface of the metal
– So, increasing the number of electrons striking the metal will not increase the kinetic energy of the electrons, it will increase the number of photoelectrons emitted
Photoelectric Current
- The photoelectric current is the number of photoelectrons emitted per second
- Photoelectric current is proportional to the intensity of the radiation incident on the surface of the metal
- This is because intensity is proportional to the number of photons striking the metal per second
- Since each photoelectron absorbs a single photon, the photoelectric current must be proportional to the intensity of the incident radiation
