ENERGY & MASS EQUIVALENCE
- Einstein showed in his theory of relativity that matter can be considered a form of energy and hence, he proposed:
- Mass can be converted into energy
- Energy can be converted into mass
- This is known as mass-energy equivalence, and can be summarised by the equation:
$
\mathbf{E}=\mathbf{m c}^2
$
- Where:
- $E=$ energy $(\mathrm{J})$
- $\mathrm{m}=$ mass $(\mathrm{kg})$
- $c=$ the speed of light $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- Some examples of mass-energy equivalence are:
- The fusion of hydrogen into helium in the centre of the sun
- The fission of uranium in nuclear power plants
- Nuclear weapons
- High-energy particle collisions in particle accelerators
NUCLEAR EQUATIONS
Representing Simple Nuclear Reactions
- Nuclear reactions can be represented by balanced equations of nuclei in the AZX form
- The top number A represents the nucleon number or the mass number
- Nucleon number $(A)=$ total number of protons and neutrons in the nucleus
- The lower number $Z$ represents the proton or atomic number
- Proton number $(\mathbf{Z})=$ total number of protons in the nucleus
Worked example: Simple nuclear reactions
When a neutron is captured by a uranium-235 nucleus, the outcome may be represented by the nuclear equation:
$
{ }_{92}^{235} \mathrm{U}+{ }_0^1 \mathrm{n} \longrightarrow{ }_{42}^{95} \mathrm{Mo}+{ }_{57}^{139} \mathrm{La}+\mathrm{x}_0^1 \mathrm{n}+{ }_{-1}^0 \mathrm{e}
$
What is the value of $x$ ?Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Step 1:
Balance the nucleon numbers (the top number)
$
235+1=95+139+x(1)+7(0)
$
Step 2:
Rearrange to find the value of $x$
$
x=235+1-95-139=2
$
MASS DEFECT & BINDING ENERGY
- Experiments into nuclear structure have found that the total mass of a nucleus is less than the sum of the masses of its constituent nucleons
- This difference in mass is known as the mass defect
- Mass defect is defined as:
The difference between an atom’s mass and the sum of the masses of its protons and neutrons
- The mass defect $\Delta \mathrm{m}$ of a nucleus can be calculated using:
$
\Delta m=Z m_p+(A-Z) m_n-m_{\text {total }}
$
- Where:
- $\mathrm{Z}=$ proton number
- $\mathrm{A}=$ nucleon number
- $\mathrm{m}_{\mathrm{p}}=$ mass of a proton $(\mathrm{kg})$
- $\mathrm{m}_{\mathrm{n}}=$ mass of a neutron $(\mathrm{kg})$
- $\mathrm{m}_{\text {total }}=$ measured mass of the nucleus $(\mathrm{kg})$
- Due to the equivalence of mass and energy, this decrease in mass implies that energy is released in the process
- Since nuclei are made up of neutrons and protons, there are forces of repulsion between the positive protons
- Therefore, it takes energy, ie. the binding energy, to hold nucleons together as a nucleus
- Binding energy is defined as:
The energy required to break a nucleus into its constituent protons and neutrons - Energy and mass are proportional, so, the total energy of a nucleus is less than the sum of the energies of its constituent nucleons
- The formation of a nucleus from a system of isolated protons and neutrons is therefore an exothermic reaction – meaning that it releases energy
- This can be calculated using the equation:
$
E=\Delta \mathrm{mc}^2
$
Binding Energy per Nucleon
- In order to compare nuclear stability, it is more useful to look at the binding energy per nucleon
- The binding energy per nucleon is defined as:
The binding energy of a nucleus divided by the number of nucleons in the nucleus - A higher binding energy per nucleon indicates a higher stability
- In other words, it requires more energy to pull the nucleus apart
- Iron $(A=56$ ) has the highest binding energy per nucleon, which makes it the most stable of all the elements
Key Features of the Graph
- At low values of $A$ :
- Nuclei tend to have a lower binding energy per nucleon, hence, they are generally less stable
- This means the lightest elements have weaker electrostatic forces and are the most likely to undergo fusion
- Helium $\left({ }^4 \mathrm{He}\right)$, carbon $\left({ }^{12} \mathrm{C}\right)$ and oxygen $\left({ }^{16} \mathrm{O}\right)$ do not fit the trend
- Helium-4 is a particularly stable nucleus hence it has a high binding energy per nucleon
- Carbon-12 and oxygen-16 can be considered to be three and four helium nuclei, respectively, bound together
- At high values of $A$ :
- The general binding energy per nucleon is high and gradually decreases with A
- This means the heaviest elements are the most unstable and likely to undergo fission
Worked example: Binding energy of iron
What is the binding energy per nucleon of iron-56 $\left.{ }_{26}^{56} \mathrm{Fe}\right)$ in $\mathrm{MeV}$ ?
Mass of a neutron $=1.675 \times 10^{-27} \mathrm{~kg}$
Mass of a proton $=1.673 \times 10^{-27} \mathrm{~kg}$
Mass of ${ }_{26}^{56} \mathrm{Fe}$ nucleus $=9.288 \times 10^{-26} \mathrm{~kg}$
Answer/Explanation
Step 1:
Calculate the mass defect
Number of protons, $Z=26$
Number of neutrons, $A-Z=56-26=30$
Mass defect, $\Delta m=Z m_p+(A-Z) m_n-m_{\text {total }}$
$
\begin{gathered}
\Delta \mathrm{m}=\left(26 \times 1.673 \times 10^{-27}\right)+\left(30 \times 1.675 \times 10^{-27}\right)-\left(9.288 \times 10^{-26}\right) \\
\Delta \mathrm{m}=8.680 \times 10^{-28} \mathrm{~kg}
\end{gathered}
$
Step 2:
Calculate the binding energy of the nucleus
Binding energy, $E=\Delta \mathrm{mc}^2$
$
E=\left(8.680 \times 10^{-28}\right) \times\left(3.00 \times 10^8\right)^2=7.812 \times 10^{-11} \mathrm{~J}
$
Step 3:
Calculate the binding energy per nucleon
$
\begin{aligned}
& \text { Binding energy per nucleon }=\frac{E}{A} \\
& \frac{E}{A}=\frac{7.812 \times 10^{-11}}{56}=1.395 \times 10^{-12} \mathrm{~J}
\end{aligned}
$
Step 4:
Convert to $\mathrm{MeV}$
$
\begin{gathered}
\mathrm{J} \rightarrow \mathrm{eV} \text { : divide by } 1.6 \times 10^{-19} \\
\mathrm{eV} \rightarrow \mathrm{MeV}: \text { divide by } 10^6
\end{gathered}
$
Binding energy per nucleon $=\frac{1.395 \times 10^{-12}}{1.6 \times 10^{-19}}=8718750 \mathrm{eV}=8.7 \mathrm{MeV}$ (2 s.f.)
Exam Tip
Checklist on what to include (and what not to include) in an exam question asking you to draw a graph of binding energy per nucleon against nucleon number:
- You will be expected to draw the best fit curve AND a cross to show the anomaly that is helium
- Do not begin your curve at $\mathrm{A}=0$, this is not a nucleus!
- Make sure to correctly label both axes AND units for binding energy per nucleon
- You will be expected to include numbers on the axes, mainly at the peak to show the position of iron $\left({ }^{56} \mathrm{Fe}\right)$
NUCLEAR FUSION & FISSION
- Nuclear Fusion
- Fusion is defined as:
The fusing together of two small nuclei to produce a larger nucleus - Low mass nuclei (such as hydrogen and helium) can undergo fusion and release energy
- For two nuclei to fuse, both nuclei must have high kinetic energy
- This is because the protons inside the nuclei are positively charged, which means that they repel one another
- It takes a great deal of energy to overcome the electrostatic force, so this is why it is can only be achieved in an extremely high-energy environment, such as star’s core
- When two protons fuse, the element deuterium is produced
- In the centre of stars, the deuterium combines with a tritium nucleus to form a helium nucleus, plus the release of energy, which provides fuel for the star to continue burning
Nuclear Fission
- Fission is defined as:
The splitting of a large atomic nucleus into smaller nuclei - High mass nuclei (such as uranium) can undergo fission and release energy
- Fission must first be induced by firing neutrons at a nucleus
- When the nucleus is struck by a neutron, it splits into two, or more, daughter nuclei
- During fission, neutrons are ejected from the nucleus, which in turn, can collide with other nuclei which triggers a cascade effect
- This leads to a chain reaction which lasts until all of the material has undergone fission, or the reaction is halted by a moderator
- Nuclear fission is the process which produces energy in nuclear power stations, where it is well controlled
- When nuclear fission is not controlled, the chain reaction can cascade to produce the effects of a nuclear bomb
Exam Tip
When an atom undergoes nuclear fission, take note that extra neutrons are ejected by the nucleus and not from the fission products
Significance of Binding Energy per Nucleon
- At low values of $A$ :
- Attractive nuclear forces between nucleons dominate over repulsive electrostatic forces between protons
- In the right conditions, nuclei undergo fusion
- In fusion, the mass of the nucleus that is created is slightly less than the total mass of the original nuclei
- The mass defect is equal to the binding energy that is released, since the nucleus that is formed is more stable
- At high values of $A$ :
- Repulsive electrostatic forces between forces begin to dominate, and these forces tend to break apart the nucleus rather than hold it together
- In the right conditions, nuclei undergo fission
- In fission, an unstable nucleus is converted into more stable nuclei with a smaller total mass
- This difference in mass, the mass defect, is equal to the binding energy that is released
CALCULATING ENERGY RELEASED IN NUCLEAR REACTIONS
- The binding energy is equal to the amount of energy released in forming the nucleus, and can be calculated using:
$
E=(\Delta m) c^2
$
- Where:
- $E=$ Binding energy released (J)
- $\Delta \mathrm{m}=$ mass defect $(\mathrm{kg})$
- $c=$ speed of light $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
- The daughter nuclei produced as a result of both fission and fusion have a higher binding energy per nucleon than the parent nuclei
- Therefore, energy is released as a result of the mass difference between the parent nuclei and the daughter nuclei
Worked example: Calculating energy released
When Uranium-235 nuclei are fissioned by slow-moving neutrons, two possible reactions are:
Reaction 1: ${ }_{92}^{235} \mathrm{U}+{ }_0^1 \mathrm{n} \rightarrow{ }_{54}^{139} \mathrm{Xe}+{ }_{38}^{95} \mathrm{Sr}+2{ }_0^1 \mathrm{n}+$ energy
Reaction 2: ${ }_{92}^{235} U+{ }_0^1 n \rightarrow 2{ }_{46}^{116} P d+x c+$ energy
a) For reaction 2, identify the particle $c$ and state the number $\mathrm{x}$ of such particles generated in the reaction.
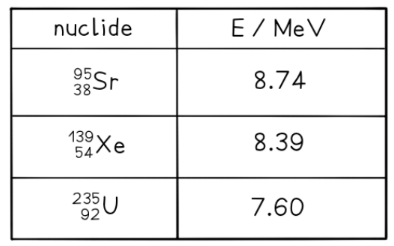
b) The binding energy per nucleon $E$ for a number of nuclides is given by the table below. Use the table to show that the energy produced in reaction 1 is about $210 \mathrm{MeV}$.
c) The energy produced in reaction 2 is $163 \mathrm{MeV}$. Suggest, with supporting reason, which one of the two reactions is more likely to happen.
Answer/Explanation
Part (a)
Step 1:
Balance the number of protons on each side (bottom number)
$92=(2 \times 46)+x n_p$ (where $n_p$ is the number of protons in $\left.c\right)$
$
\mathrm{xn}_{\mathrm{p}}=92-92=0
$
Therefore, $c$ must be a neutron
Step 2:
Balance the number of nucleons on each side
$
\begin{aligned}
& 235+1=(2 \times 116)+x \\
& x=235+1-232=4
\end{aligned}
$
Therefore, 4 neutrons are generated in the reaction
Part (b)
Step 1: $\quad$ Find the binding energy of each nucleus
Total binding energy of each nucleus $=$ Binding energy per nucleon $\times$ Mass number
Binding energy of ${ }^{95} \mathrm{Sr}=8.74 \times 95=830.3 \mathrm{MeV}$
Binding energy of ${ }^{139} \mathrm{Xe}=8.39 \times 139=1166.21 \mathrm{MeV}$
Binding energy of ${ }^{235} \mathrm{U}=7.60 \times 235=1786 \mathrm{MeV}$
Step 2: $\quad$ Calculate the difference in energy between the products and reactants
Energy released in reaction $1=\mathrm{E}_{\mathrm{sr}}+\mathrm{E}_{\mathrm{xe}}-\mathrm{E}_{\mathrm{u}}$
Energy released in reaction $1=830.3+1166.21-1786$
Energy released in reaction $1=210.5 \mathrm{MeV}$
Part (c)
- Since reaction 1 releases more energy than reaction 2, its end products will have a higher binding energy per nucleon
- Hence they will be more stable
- This is because the more energy is released, the further it moves up the graph of binding energy per nucleon against nucleon number (A)
- Since at high values of $A$, binding energy per nucleon gradually decreases with $A$
- Nuclear reactions will tend to favour the more stable route, therefore, reaction 1 is more likely to happen
