Momentum as the product of mass and velocity
Momentum or Linear momentum or translational momentum is the product of the mass and velocity of an object.
Momentum $=$ mass $\mathrm{x}$ velocity
For example, a heavy truck moving fast has a large momentum-it takes a large and prolonged force to get the truck up to this speed, and it takes a large and prolonged force to bring it to a stop afterwards. If the truck were lighter, or moving slower, then it would have less momentum.
- Like velocity, linear momentum is a vector quantity, possessing a direction as well as a magnitude:
- Units: $\mathrm{kgms}^{-1}$ or Ns
Force as a rate of change of Momentum
• Consider a body of mass m, initially moving with a velocity of magnitude u. A force F acts on the body and causes it to accelerate to a final velocity of magnitude v.
• We can write Newton’s second law in the form
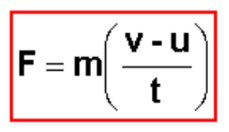
• and a simple rearrangement shows the relation between force and momentum
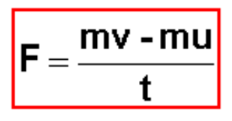
Remember, momentum = mass x velocity.
• Now, mv is the final momentum of the body and mu is the initial momentum of the body. Therefore, we have
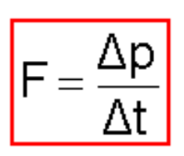
Force = rate of change of momentum
Momentum as the product of mass and velocity
Momentum or Linear momentum or translational momentum is the product of the mass and velocity of an object.
Momentum $=$ mass $x$ velocity
For example, a heavy truck moving fast has a large momentum – it takes a large and prolonged force to get the truck up to this speed, and it takes a large and prolonged force to bring it to a stop afterwards. If the truck were lighter, or moving slower, then it would have less momentum.
- Like velocity, linear momentum is a vector quantity, possessing a direction as well as a magnitude:
- Units: kgms $^{-1}$ or Ns
Principle of Conservation of Momentum
- The Principle of the Conservation of Momentum states that: if objects collide, the total momentum before the collision is the same as the total momentum after the collision (provided that no external forces – for example, friction – act on the system).
- Of course, energy is also conserved in any collision, but it isn’t always conserved in the form of kinetic energy.
Case 1
• To do any calculations for momentum, there are some simple rules to follow to make it easy:
• Always decide which direction is positive and which is negative, then stick to it.
• Always remember that the total momentum before the collision will be the same as the total momentum after the collision.
• So,
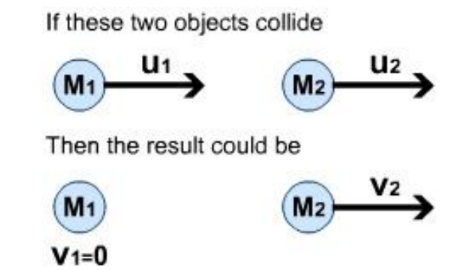
- The conservation of momentum states:
- Momentum $_{\text {before }}=$ Momentum $\mathrm{after}$
- So, $\left(P_1+P_2\right)$ before $=\left(P_1+P_2\right)$ after
- Or, $m_1 u_1+m_2 u_2=m_1 v_1+m_2 v_2$
- But notice that in this example, $\mathbf{v}_{\mathbf{1}}=\mathbf{0}$. So that term cancels and makes finding an answer much easier.
Case 2
• If the objects change direction in the collision or are going in different directions before the collision, make sure that you have got the signs for the velocities and therefore the momentums correct.
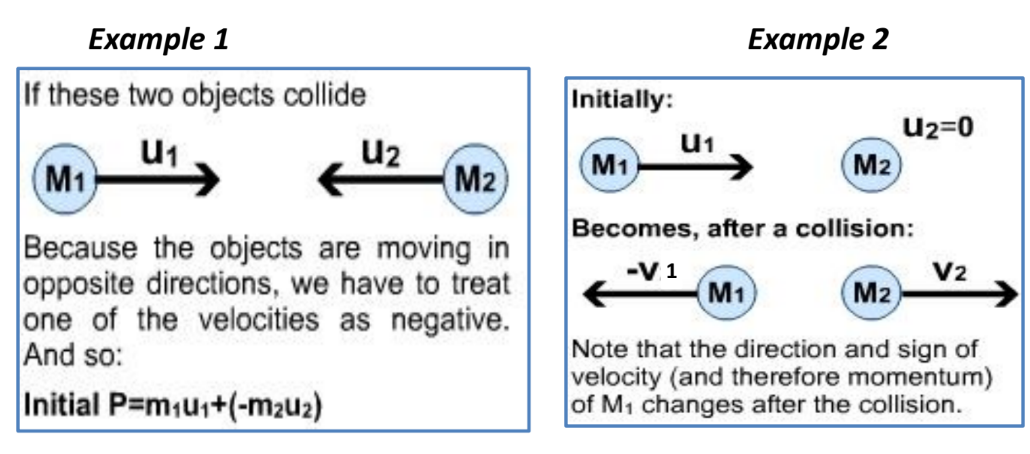
Case 3
• When objects bounce back after a collision, be careful about the change in momentum.
Example
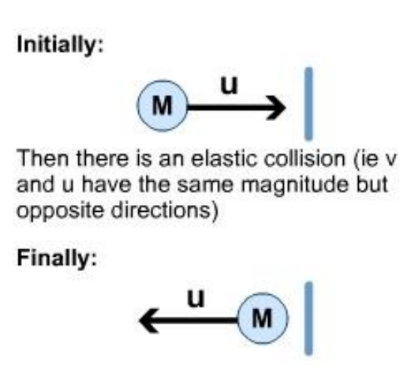
So change in momentum = final $P$ – initial $P$
$
\begin{aligned}
& =-m u-(+m u) \\
& =-2 m u
\end{aligned}
$
Explosions
- Explosions are a special type of collision. Momentum is conserved in an explosion. This is made easier by the fact that usually, the momentum before an explosion is zero. The Principle of the Conservation of Momentum states that the momentum after the explosion must therefore be zero as well.
What is the momentum of the Universe?
• If the universe began with a Big Bang (for instance – an explosion), the momentum of the universe before the explosion was zero.
So what is its momentum ?
Force can be defined as the rate of change of momentum as:
$
F=m a
$
But, $a=\frac{v-u}{t}$
$
\text { So, } F=m\left(\frac{v-u}{t}\right)=\frac{m v-m u}{t}=\frac{\text { change in momentum }}{\text { time }}
$
Principle of Conservation of Momentum Elastic and Inelastic collisions
- Perfectly Elastic collisions
- All momentum is conserved
- Kinetic energy is conserved as well.
- Relative speed of approach = relative speed of separation.
- (So if one is catching the other at $10 \mathrm{~m} / \mathrm{s}$ before the collision, it will be moving apart from it at $10 \mathrm{~m} / \mathrm{s}$ after the collision)
- Perfectly Elastic collisions are surprisingly common. All collisions between atoms are Perfectly Elastic according to the Kinetic Theory of Gases.Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
- Perfectly Inelastic collisions
- All momentum is conserved (as always).
- Kinetic energy is not conserved.
- The relative speed of separation is zero.
- IIn other words, that means the objects stick together after the collision, they will move together, so just consider them as one object whose mass is the same as that of the two original masses combined).
Why is kinetic energy not conserved while momentum is conserved in a perfectly inelastic collision?
- It goes into heat, sound, work done to deform the colliding bodies etc. Other forms of energy, in other words.
- Momentum is not a type of energy. Momentum and energy are totally different physical quantities with different physical dimensions. (Energy is the capacity to do work)
Conservation of momentum in a system occurs provided that there are no external forces acting on a system. This is a consequence of Newton’s 2nd law and Newton’s 3rd law. Newton’s 2 nd law says that the net force acting on a body is equal to the rate of change of its momentum.
This is the full, general statement of the 2 nd law. $F=\Delta p / \Delta t$. If the mass of the body is constant, this reduces to $\mathrm{F}=$ $\mathrm{m}(\Delta \mathrm{v} / \Delta \mathrm{t})=\mathrm{ma}$. Therefore, if a net force acts on an object, its momentum will change with time. If there is no net force,then its momentum will not change.
How and when momentum is conserved ?
- Now, consider a system of interacting particles. The particles are moving around randomly. Every once in a while, two particles (1 and 2) may collide. While this is happening, particle 1 exerts a force on particle 2. However, Newton’s 3rd law says that particle 2 must therefore, at the same time, exert a force on particle 1 of equal strength and opposite direction. These forces are also exerted over the same time interval (while the particles are in contact). Therefore, the change in momentum of particle 1 will be equal in magnitude and opposite in direction to the change in momentum of particle 2.
- These two momentum changes therefore cancel each other out. Each particle may individually change its momentum, but there will be no change to the total momentum of the system. In other words, since Newton’s 3rd says that these internal forces always occur in matched “action-reaction” pairs, they cannot ever cause a change to the overall momentum of the system. Only an external force (a force from something that is not part of the system of particles) can cause a change in the total momentum of the system. In the absence of a net external force, $F_{\text {tot }}=0$ and hence $\Delta p_{\text {tot }}=0$. In the absence of external forces, momentum is conserved.
