Newtonian Mechanics
- Energy possessed by a body is the capacity of the body to do work.
- State the principle of conservation of energy. Energy can neither be created nor destroyed, but can be converted from one form to another (or others).
- The total amount of energy in any closed system is constant.
- Energy and work are both scalar quantities, and have the unit Joule.
Work in terms of the product of a force and displacement in the direction of the force
In physics, work is done when a force moves its point of application so that some resolved part of the displacement lies along the direction of the force.
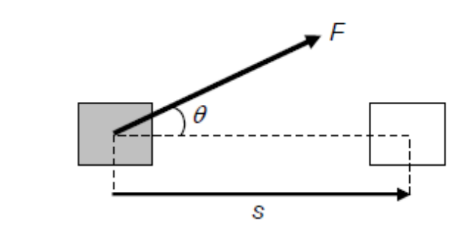
1. Define work.
The work $W$ done on an object by an agent exerting a constant force $F$ on the object is defined as the product of the force and the displacement in the direction of the force.
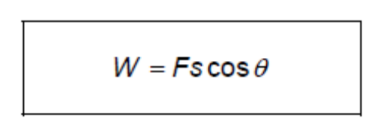
where
$W$ is the work done on the object by the constant force $F$ (joule, J)
$F$ is the constant force acting on the object (Newton, N)
$s$ is the displacement of the object (metre, $\mathrm{m}$ )
$\theta$ is the angle between $F$ and $s$ (degree, ${ }^{\circ}$ )
In cases, where no angle is given, you may use the equation W = Fs
Unit of Work
The S.I. unit for work is the joule
One joule $(1 \mathrm{~J})$ is defined as the work done by a constant force of one newton $(1 \mathrm{~N})$ on an object when the object moves one metre $(1 \mathrm{~m})$ in the direction of the force.
$
1 \mathrm{~J} \equiv(1 \mathrm{~N})(1 \mathrm{~m})=1 \mathrm{~N} \mathrm{~m}
$
The unit Newton metre $(\mathrm{N} \mathrm{m})$ is usually used for moment, while Joule $(\mathrm{J})$ is usually used for work.
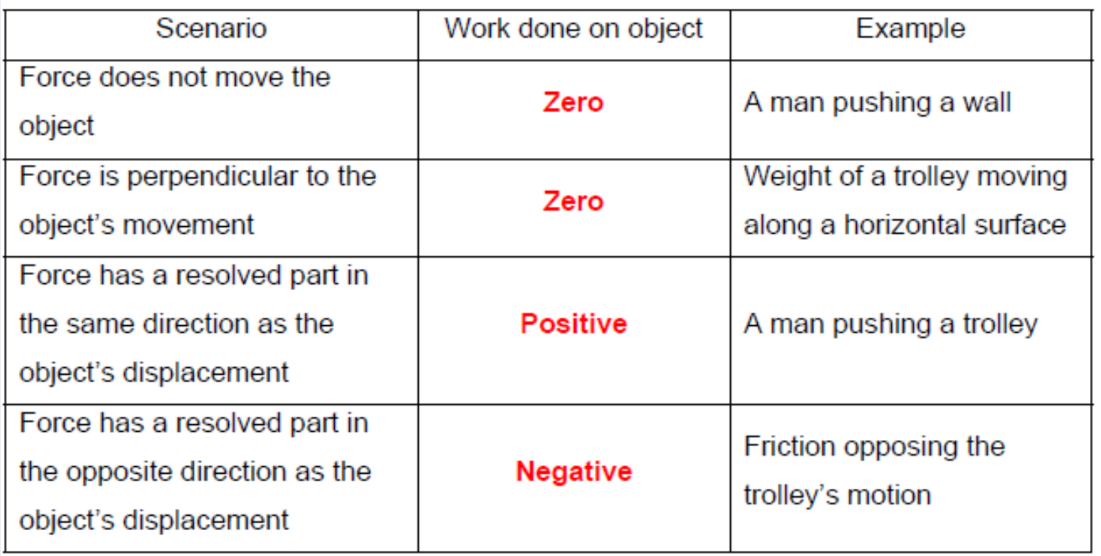
Even though work is a scalar, it can be positive or negative.
In the above examples, positive work done on an object increases the kinetic energy of the trolley, while negative work done ___decreases __ its kinetic energy. Zero work done means the kinetic energy remains constant
Work done by a constant force
Sample problem – 1.
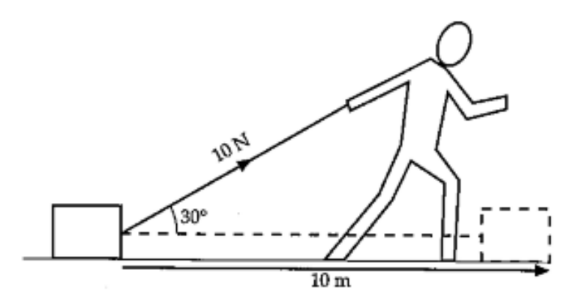
- The following are examples of work done by a constant force.
(a) Work done by the man on a box (Fig 6.3).
$
\begin{aligned}
W & =F s \cos \theta \\
& =(10)(10) \cos 30^{\circ} \\
& =86.6 \mathrm{~J} \\
& =87 \mathrm{~J}
\end{aligned}
$
Sample problem 2 – Solve it!
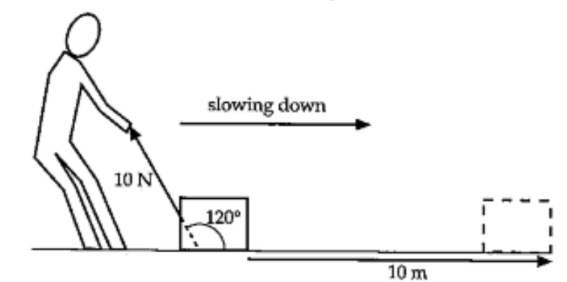
(b) Work done by the man in opposing the sliding box (Fig 6.4)
$
\begin{aligned}
W & =F s \cos \theta \\
& =(10)(10) \cos 120^{\circ} \\
& =-50 \mathrm{~J}
\end{aligned}
$
Sample problem 3 – Solve it!
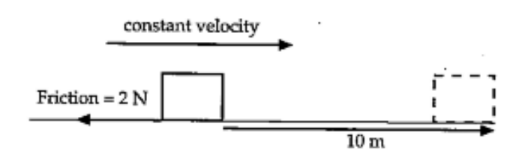
(c) Work done by the frictional force in opposing the sliding box (Fig 6.5).
$
\begin{aligned}
W & =F s \cos \theta \\
& =(2)(10) \cos 180^{\circ} \\
& =-20 \mathrm{~J}
\end{aligned}
$
Sample problem 4 – Solve it !
A man pushes a box of mass $5 \mathrm{~kg}$ with a force of $2 \mathrm{~N}$ along a horizontal frictionless surface. The box is moved through a distance $3 \mathrm{~m}$.
Calculate the work done on the box by
(a) the pushing force;
(b) the normal contact force;
(c) the weight of the box.
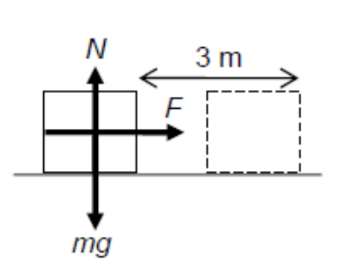
(a) $W=F s \cos \theta=2 \times 3=6 \mathrm{~J}$
(b) $W=0 \mathrm{~J}$ (force perpendicular to displacement)
(c) $W=0 \mathrm{~J}$
Example 5 – Solve it !
A block is pulled along a rough horizontal surface by a rope pointing at $60^{\circ}$ above the horizontal. The tension in the rope is $10 \mathrm{~N}$ and the frictional force is $5 \mathrm{~N}$. The block moves a distance of $2 \mathrm{~m}$ along the surface.
Calculate the work done on the box by
(a) the tension in the rope;
(b) the frictional force.
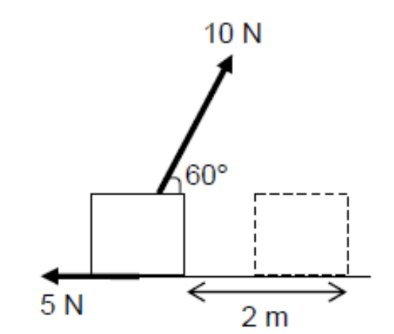
(a) $W=F s \cos \theta=\left(10 \cos 60^{\circ}\right) 2$
$
=10 \mathrm{~J}
$
(b) $W=(-5) 2=-10 \mathrm{~J}$
Example 6 – Solve it !
• How much work is done by a person who uses a force of 27.5N to move a trolley 12.3m?
$\begin{aligned} W & =F \times d=(27.5 \mathrm{~N})(12.3 \mathrm{~m}) \\ & =338.25 \mathrm{~J}\end{aligned}$$\begin{aligned} W & =F \times d=(27.5 \mathrm{~N})(12.3 \mathrm{~m}) \\ & =338.25 \mathrm{~J}\end{aligned}$
Special case
Suppose a force $F$ is acting on an object along the $x$-direction and the object moves a distance $\left(x_2-x_1\right)$ along the same direction.
If $F$ is constant,
work done is given by $W=F\left(x_2-x_1\right)$
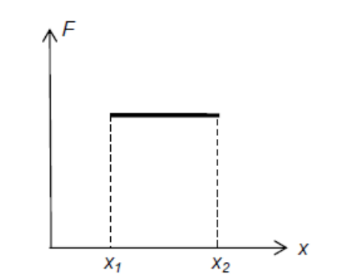
Work done $=$ area under force-displacement __ graph
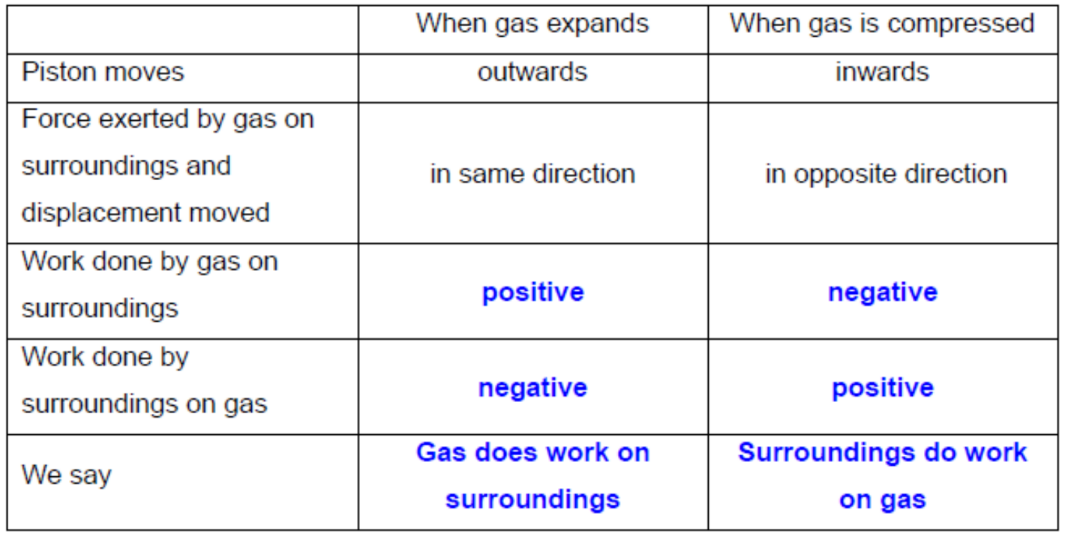
For work done by a gas which is expanding against a constant external pressure

Symbols
$F$ is the force exerted by external pressure on piston
$p$ is the constant external pressure
$\Delta x$ is the distance moved by piston
$A$ is the cross-sectional area of piston
For a piston with a cross-sectional area $A$, the force $F$ acting normal to it is given by $F=p A$.
For a gas with pressure = external pressure $\mathrm{p}$, if the piston is allowed to move outwards slowly by a displacement $\Delta x$, the gas will expand against the constant external pressure $p$, and $\mathrm{F}_{\text {gas }}=\mathrm{F}$.
For a gas with pressure $=$ external pressure $\mathrm{p}$, if the piston is allowed to move outwards slowly by a displacement $\Delta x$, the gas will expand against the constant external pressure $p$, and $\mathrm{F}_{\text {gas }}=\mathrm{F}$.
The work done $W$ by the gas against this constant pressure $p$ is given by $W=F \Delta x$ $=(p A) \Delta x=p(A \Delta x)=p \Delta V$ where $\Delta V$ is the change in volume.
Hence, when a gas expands with a change in volume $\Delta V$ against constant pressure $p$, work done by gas is given by:
(1) 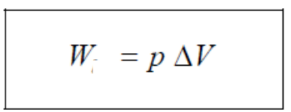
where $\quad W \cdots$ is the work done by gas $(\mathrm{J})$
$p$ is the external pressure $(\mathrm{Pa})$
$\Delta V$ is the change in volume of the gas $\left(\mathrm{m}^3\right)$ Note: $\Delta V=V_{\text {final }}-V_{\text {intital }}$
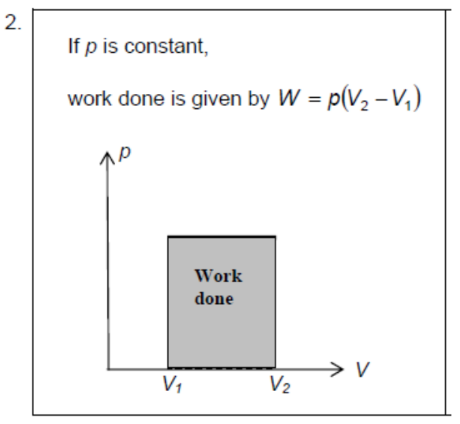
Work done $=$ area under pressure-volume graph
3.
Try to solve it !
A gas in a cylinder is kept at a constant pressure of $1.1 \times 10^5 \mathrm{~Pa}$. The gas is heated and expands by $25 \mathrm{~cm}^3$.
Calculate the work done by the gas.
$
\begin{aligned}
& 1 \mathrm{~cm}=10^{-2} \mathrm{~m} \\
& 1 \mathrm{~cm}^3=10^{-6} \mathrm{~m}^3 \\
& W=p \Delta V=1.1 \times 10^5 \times 25 \times 10^{-6}=2.75 \mathrm{~J}
\end{aligned}
$
Derive from Equations of motion (KE)
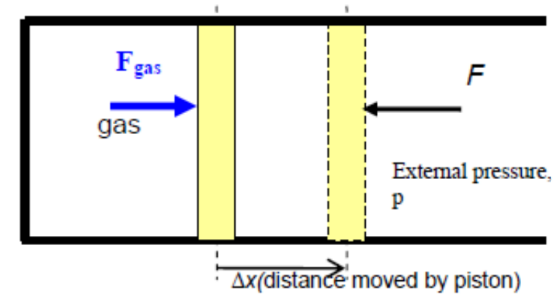
1. The kinetic energy (K.E.) is a positive scalar quantity that represents the energy associated with the body due to its motion.
It is equal to the work done by the resultant force in accelerating the body from rest to an instantaneous speed $v$.
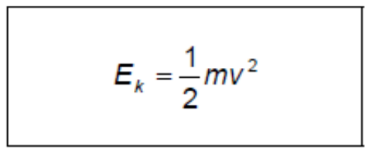
where
$E_k$ is the kinetic energy of the body moving at speed $v(\mathrm{~J})$
$m$ is the mass of the body $(\mathrm{kg})$
$v$ is the speed of the body $\left(\mathrm{m} \mathrm{s}^{-1}\right)$
Derive, from the equations of motion, the formula $E_k=1 / 2 m v^2$.
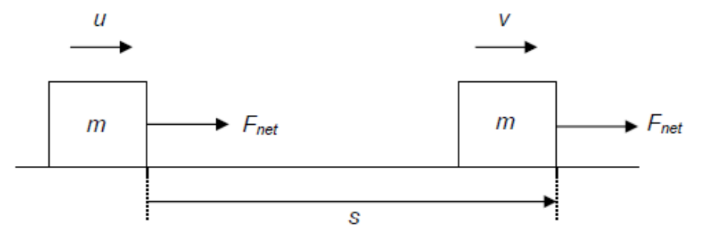
Body initially at rest, $u=0$ :
work done by net force = change in K.E. of body
$
\begin{gathered}
\left(F_{n e t}\right) s=E_k \\
\text { mas }=E_k
\end{gathered}
$
Using $v^2=u^2+2$ as: $\quad 1 / 2 m v^2-1 / 2 m(0)^2=E_k$
$
\therefore \quad E_k=\frac{1}{2} m v^2
$
Note:
1. $E_k$ is a scalar quantity and has the same units as work i.e. joules, J.
2. Work done by net force $=$ change in K.E. of body $\left(W=1 / 2 m v^2-1 / 2 m u^2\right)$
Sample problem 1 – Solve it !
A car of mass $800 \mathrm{~kg}$ and moving at $30 \mathrm{~m} \mathrm{~s}^{-1}$ along a horizontal road is brought to rest by a constant retarding force of $5000 \mathrm{~N}$.
Calculate the distance travelled by the car in coming to rest.
Using work done = change in K.E.:
$
\begin{aligned}
& W=\frac{1}{2} m v^2-\frac{1}{2} m u^2 \\
& (-5000) s=0-\frac{1}{2}(800)(30)^2 \\
& s=72 m
\end{aligned}
$
Using kinematics equation:
$
\begin{aligned}
& v^2=u^2+2 a s \\
& 0=30^2+2\left(\frac{-5000}{800}\right) s \\
& s=72 \mathrm{~m}
\end{aligned}
$
Energy in different forms, its conversion and conservation, and apply the principle of energy conservation to simple examples
Types of energy and their sources:

Renewable and Non-renewable energy
Renewable sources of energy are those that can be replaced or replenished each day by the Earth’s natural processes. Eg. wind power, geothermal, solar energy, tidal energy.
Non-renewable sources of energy are those that are finite or exhaustible because it takes several million years to replace them eg. fossil fuels like coal, oil and natural gas, energy sources that are tapped from minerals eg. nuclear energy from the fission of Uranium nuclei.
