Gravitational potential energy, Electric potential energy and Elastic potential energy
1. Potential energy (P.E.) is the energy possessed by a system by virtue of the relative positions of its component parts.
2. Gravitational potential energy (G.P.E.) is associated with the interaction between bodies due to their masses.
3. Electric potential energy is associated with the interaction between bodies due to their electric charges
4. Elastic potential energy is possessed by an object due to its state of deformation
Give EXAMPLES of energy in different forms and its conversion
More Examples of Energy conversion
Example diver jumping off a diving board
- The diver uses his gravitational potential energy to do work in bending the diving board.
- The work done is stored as elastic potential energy, which is then converted into kinetic energy of the diver as he is pushed upwards and off the diving board.
- At the same time, some of the elastic potential energy is lost as heat and sound due to dissipative forces in the diving board.
Example burning of fossil fuel
- When fuels such as oil, coal and wood are burnt, the chemical energy stored in these materials is converted into thermal energy (heat) and light energy.
Example hammering a nail into a wooden block
- A person uses the chemical energy in his muscles to work against the gravitational pull in order to lift the hammer.
- The work done is converted into the gravitational potential energy of the hammer in its raised position.
- As the hammer falls, its gravitational potential energy is converted into kinetic energy.
- When the hammer hits the nail, its kinetic energy is used to do work in driving the nail into the wooden block, producing sound energy in the air and thermal energy in the block, nail and hammer.
Example: falling plasticine
- During impact, all kinetic energy is converted into thermal and sound energies as the plasticine is permanently deformed.
Example bouncing ball
- As the ball falls, its gravitational potential energy is converted into its kinetic energy.
- When the ball hits the ground, the ball is deformed during the collision. Its kinetic energy is converted into elastic potential energy. Some kinetic energy may be lost as thermal energy or sound energy.
- The elastic potential energy is converted back into kinetic energy as the ball regains its original shape.
- The kinetic energy is converted into gravitational potential energy as the ball bounces upwards, until it reaches its highest position.
- During the flight, presence of air resistance will cause kinetic energy to be dissipated as thermal energy, thus reducing the total energy in the ball and its subsequent height after each bounce.
Internal Energy
- Matter consists of atoms and molecules and these are made up of particles having kinetic energy and Potential energy.
- We can define the Internal energy of a system as the sum of the kinetic energy of all its constituent particles plus the sum of all the potential energy of interaction among these particles in the system.
Note: The internal energy does not include potential energy arising out of interaction between the system and it surroundings.
The implications of energy losses in practical devices and use the concept of efficiency to solve problems
1. For practical devices to work, energy input is needed. Most modern practical devices run on electrical energy (e.g. television, computer) or chemical energy (e.g. vehicle).
When a practical device works, it converts the energy input into both useful energy output and wasted energy output.
2. Efficiency of a practical device is a measure of how much useful work that device produces from a given amount of energy input.
Its value does depend on what energy output we consider as useful.
Efficiency is dimensionless and can be expressed as a ratio or percentage.

3. We can never make a practical device with $100 \%$ efficiency because:
(a) we have limited_control over physical processes (e.g. a filament bulb must heat up before it produces light, but the heat produced becomes wasted energy);
4. Sample Problem
A car has a mass of $800 \mathrm{~kg}$ and the efficiency of its engine is rated at $18 \%$. Determine the amount of fuel used to accelerate the car from rest to $60 \mathrm{~km} \mathrm{~h}^{-1}$, given that the energy supplied by 1 litre of fuel is $1.3 \times 10^8 \mathrm{~J}$.
Answer/Explanation
Note: In this case, the useful energy output is defined to be the change in kinetic energy of the car as it accelerates from rest to $60 \mathrm{kmh}^{-1}$.
Useful energy output = K.E. of car $=\frac{1}{2}(800)\left(\frac{60000}{60 \times 60}\right)^2=111111 \mathrm{~J}$
$
\begin{aligned}
\eta=\frac{\text { useful energy output }}{\text { energy input }} \times 100 \% & \Rightarrow 18 \%=\frac{111111}{\text { energy input }} \times 100 \% \\
& \Rightarrow \text { energy input }=617284 \mathrm{~J}
\end{aligned}
$
Amount of fuel $=\frac{617284}{1.3 \times 10^8}=0.0047$ litres
Derive, from the defining equation W = Fs, the formula Ep = mgh for the potential energy changes near the Earth’s surface
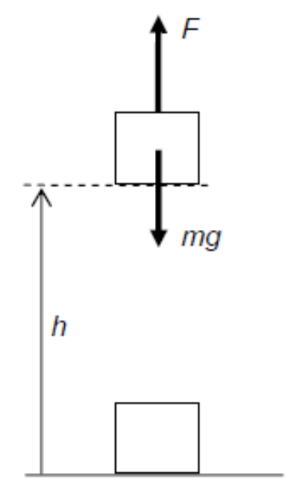
Suppose we want to lift an object of mass $m$ to a height $h$ above the ground, so that its velocity remains_constant
To do so, we must apply a force $F$ that is equal but opposite _ to the weight $m g$ of the object, where $g$ is the acceleration of free fall.
The work done $W$ by force $F$ on the object is:
$
W=F h=(m g) h
$
Since the object’s velocity is constant, its kinetic energy is also constant. Hence, by conservation of energy, the work done $W$ on the object must be equal to the gain in G.P.E. of the object.

Sample problem
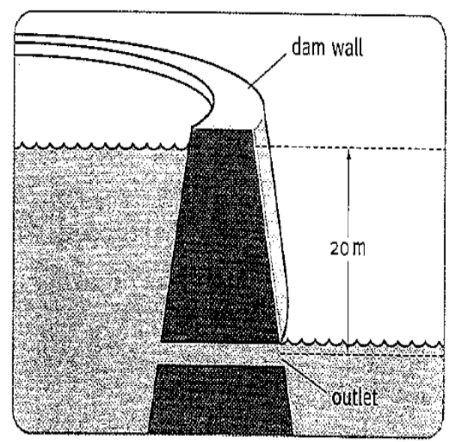
• Figure shows a dam with storage of water. The outlet of the dam is 20 m below the surface of the water in the reservoir. Water leaving the dam is moving at 16m/s. Calculate the % of G.P.E that is lost when converted into K.E.
Answer/Explanation
Solution
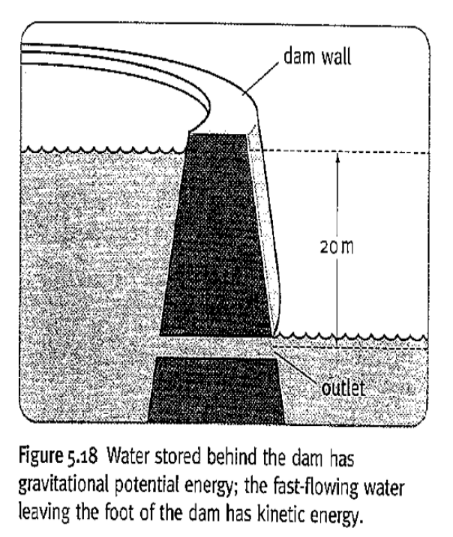
itep 1 We will picture $1 \mathrm{~kg}$ of water, starting at he surface of the lake (where it has g.p.e., but to k.e.) and flowing downwards and out at the jot (where it has k.e., but less g.p.e.). Then:
change in g.p.e. of water between surface and outflow $=m g h=1 \times 9.81 \times 20=196 \mathrm{~J}$
Step 2 Calculate the k.e. of $1 \mathrm{~kg}$ of water as it leaves the dam:
$
\begin{aligned}
\text { k.e. of water leaving dam } & =\frac{1}{2} m v^2 \\
& =\frac{1}{2} \times 1 \times(16)^2 \\
& =128 \mathrm{~J}
\end{aligned}
$
Step 3 For each kilogram of water flowing out of the dam, the loss of energy is:
$
\begin{aligned}
& \text { loss }=196-128=68 \mathrm{~J} \\
& \text { percentage loss }=\frac{68}{196} \times 100 \% \approx 35 \%
\end{aligned}
$
Define power as work done per unit time and derive power as the product of force and velocity.
Define power.
Power is defined as:
(i) the work done per unit time, or
(ii) the rate of work done, or
(iii) the rate of energy conversion.

where $\quad P$ is the power (watt, W)
$W$ is the work done (joule, $\mathrm{J}$ )
$E$ is the energy converted (joule, J) $t$ is the time taken (second, s)
The S.I. unit for power is the __ watt
One watt is defined as the power when one joule of work is done, or one joule of energy is converted, per second.
$
1 \mathrm{~W}=(1 \mathrm{~J}) /(1 \mathrm{~s})
$
3. Derive power as the product of force and velocity.
Suppose a constant force $F$ displaces an object, moving at a constant velocity $v$, by a distance $s$ over a time interval $t$, and that $F, v$ and $s$ all point along the same line.
$
P=\frac{W}{t}=\frac{F S}{t}=F\left(\frac{S}{t}\right)=F V
$
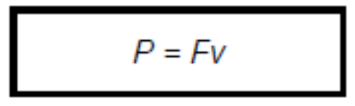
4. If force $F$ and/or velocity $v$ is/are not constant, then
(i) the average power $\langle P\rangle$ is given by $\langle P\rangle=\frac{\text { total work done }}{\text { total time taken }}$
(ii) the instantaneous power is given by $P=F V$ where $F$ and $v$ take the values at the instant considered
Sample problem 1
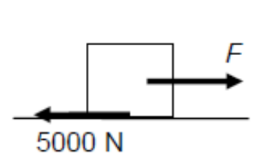
A car moves along a horizontal road at a constant velocity of $15 \mathrm{~m} \mathrm{~s}^{-1}$. If the total resistive force experienced by the car is $5000 \mathrm{~N}$, calculate the power output of the car’s engine.
Answer/Explanation
At constant velocity, $F_{\text {net }}=0$
$
\begin{aligned}
\therefore & \mathrm{F}=5000 \mathrm{~N} \\
P & =F V \\
& =(5000)(15) \\
& =75000 \mathrm{~W}
\end{aligned}
$
Sample problem 2 – Solve it!
A trolley of mass $7 \mathrm{~kg}$ is initially rest at $t=0 \mathrm{~s}$.
A cyborg pushes this trolley with a constant force of $95 \mathrm{~N}$ along a horizontal floor. The frictional force acting on the trolley is $11 \mathrm{~N}$.
Calculate
(i) the acceleration of the trolley;
(ii) the speed of the trolley at $t=4 \mathrm{~s}$;
(iii) the kinetic energy of the trolley at $t=4 \mathrm{~s}$;
(iv) the distance travelled during the first $4 \mathrm{~s}$;
(v) the instantaneous power supplied to the trolley by the cyborg at $t=4 \mathrm{~s}$;
(vi) the average power supplied to the trolley by the cyborg during the first $4 \mathrm{~s}$;
(vii) the average power dissipated by friction during the first $4 \mathrm{~s}$;
(viii) the net average power gained by the trolley during the first $4 \mathrm{~s}$, and hence, the total energy gained by the trolley during the first $4 \mathrm{~s}$.
Answer/Explanation
solution
(i) $F_{\text {net }}=m a \Rightarrow 95-11=7 a \Rightarrow a=12 \mathrm{~m} \mathrm{~s}^{-2}$
(ii) $v=u+a t=0+12(4)=48 \mathrm{~m} \mathrm{~s}^{-1}$
(iii) $E_k=1 / 2 m v^2=1 / 2(7)(48)^2=8064 \mathrm{~J}$
(iv) $s=u t+1 / 2 a t^2=0+1 / 2(12)(4)^2=96 \mathrm{~m}$
(v) $P=F v=(95)(48)=4560 \mathrm{~W}$
(vi) $\left\langle P_{\text {supplied }}\right\rangle=1 / 2(4560)=2280 \mathrm{~W}$
(vii) $\left\langle P_{\text {dissipated }}\right\rangle=\frac{W_{\text {friction }}}{\Delta t}=\frac{F_r s}{\Delta t}=\frac{(11)(96)}{4}=264 \mathrm{~W}$
(viii) $\left\langle P_{\text {net }}\right\rangle=2280-264=2016 \mathrm{~W}$
Check: $\left\langle P_{n e t}\right\rangle \Delta t=(2016)(4)=8064 \mathrm{~J}=$ K.E. gain by trolley
Relationship between force and potential energy in a uniform field
In a uniform field, a body experiences the same force $F$ at all points.
If this force $F$ moves the body along a distance $\Delta x$ in its direction, then the work done $W$ by this force $F$ is $W=F \Delta x$.
However, by conservation of energy, this work must be compensated by a decrease in potential energy, $-\Delta U$.
$
\begin{gathered}
W=F \Delta x=-\Delta U \\
F=-\frac{\Delta U}{\Delta x}
\end{gathered}
$
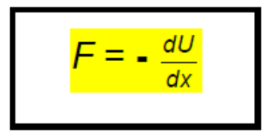
where:
- $F$ is the force acting on the point mass/charge placed at that particular point in the force field. (units: N)
- $\frac{d U}{d x}$ is the change in the potential energy of a point mass/charge with a variation of the distance from the source of the force field (units: $\mathrm{J} \mathrm{m}^{-1}$ )
Sample problem – Solve it!
A mass experiences a gravitational force of $24 \mathrm{~N}$ in a uniform gravitational field. Calculate the change in its potential energy if it moves a distance of $5.0 \mathrm{~m}$
(a) along the same direction as the gravitational force;
(b) along the opposite direction as the gravitational force;
(c) in a direction perpendicular to the gravitational force.
For each case, indicate whether the change is an increase or decrease.
Answer/Explanation
(a)
$
\begin{aligned}
\Delta U=-F \Delta x & =-24 \times 5.0 \\
& =-120 \mathrm{~J} \quad(\text { decrease) }
\end{aligned}
$
(b)
$
\begin{aligned}
\Delta U=-F \Delta x & =-24 \times(-5.0) \\
& =+120 \mathrm{~J} \quad \text { (increase) }
\end{aligned}
$
(c) $\Delta U=-F \Delta x=-24 \times 0$
$=0 \mathrm{~J} \quad$ (no change)
