Deformation of Solids
Definitions:
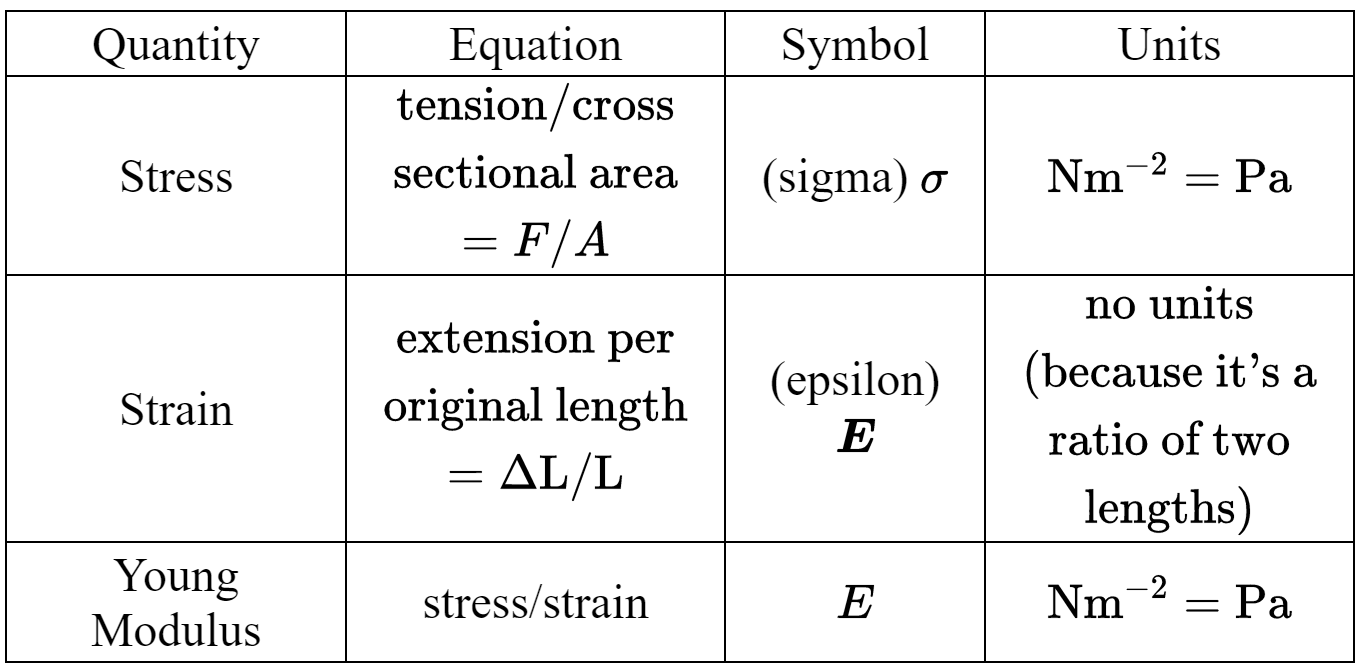
- Stress: is a measure of the force required to cause a particular deformation.
- Strain: is a measure of the degree of deformation.
- Elastic Modulus: the ratio of stress to strain Elastic Modulus $=\frac{\text { stress }}{\text { strain }}$
The elastic modulus determines the amount of force required per unit deformation. A material with large elastic modulus is difficult to deform, while one with small elastic modulus is easier to deform.
Deformation of Solids : Changes in Length
Changes in Length
To stretch or compress something you must exert a force on it at either end.
Tensile Stress is the force per unit crosssectional area exerted on the ends.
(Note the surface whose area we wish to measure is perpendicular to the force.)
Changes in Length (continued)
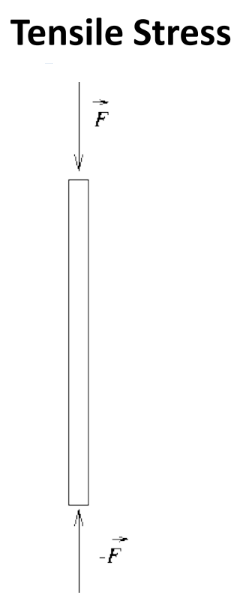
$\quad$ Tensile Strain is the fractional change in original length.
- Young’s Modulus $(Y)$ is the ratio of tensile stress to tensile strain:
- $
\mathrm{Y}=\frac{\text { tensilestress }}{\text { tensilestrain }}=\frac{F / A}{\Delta L / L_O}=\frac{F L_O}{A \Delta L}
$
where $F$ is the applied force, $L_0$ is the original length of the object, $A$ is the cross-sectional area of the object, and $\Delta L$ is the change in the length of the object. Notice that $Y$ has S.I. units of $\mathrm{N} / \mathrm{m}^2$.
Hooke’s Law
- Hooke’s Law states that, for relatively small deformations of an object, thedisplacement of the deformation is directly proportional to the deforming force or load.
- Forces can cause objects to deform.
- The way in which an object deforms depends on its dimensions, the material it is made of, the size of the force and direction of the force.
If you measure how a spring stretches (extends its length) as you apply increasing force and plot extension (e) against force (F);
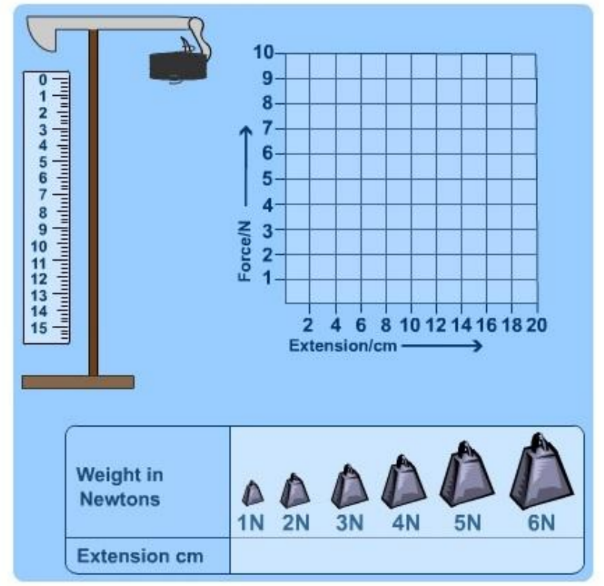
the graph will be a straight line.
Note: Because the force acting on the spring (or any object), causes stretching; it is sometimes called tension or tensile force.
This shows that Force is proportional to extension. This is Hooke’s law. It can be written as:
$
F=k e
$
Where:
$F=$ tension acting on the spring.
$e$ is extension $=\left(\mathrm{H}_0\right)$; $\mid$ is the stretched length and $\mathrm{b}_{\mathrm{b}}$ is original length, and.
$\boldsymbol{k}$ is the gradient of the graph above. It is known as the spring constant.
The above equation can be rearranged as
$
k=\frac{F}{e}
$
Spring constant $=$ Applied force/extension
The spring constant $k$ is measured in $\mathrm{Nm}^{-1}$ because it is the force per unit extension.
The value of $k$ does not change unless you change the shape of the spring or the material that the spring is made of.
A stiffer spring has a greater value for the spring constant
In fact, a vast majority of materials obey Hooke’s law for at least a part of the range of their deformation behaviour. (e.g. glass rods, metal wires).
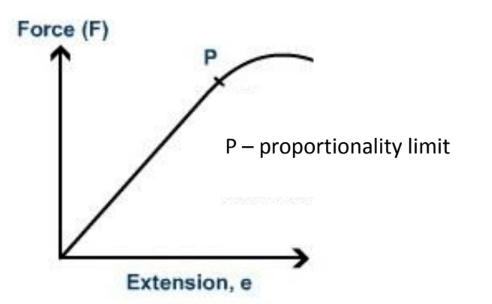
In the diagram above, if you extend the spring beyond point $P$, and then unload it completely; it won’t return to its original shape. It has been permanently deformed. We call this point the elastic limit – the limit of elastic behaviour.
If a material returns to its original size and shape when you remove the forces stretching or deforming it (reversible deformation), we say that the material is demonstrating elastic behaviour.
If deformation remains (irreversible deformation) after the forces are removed then it is a sign of plastic behaviour.
Calculating stress
- Stress
- Stress is a measure of how strong a material is. This is defined as how much force the material can stand without undergoing some sort of physical change.
- Hence, the formula for calculating stress is the same as the formula for calculating pressure: $\sigma=\frac{F}{A}$
- where $\sigma$ is stress (in Newtons per square metre but usually Pascals, commonly abbreviated Pa).
Stress causes strain.
- Applying force on an object causes it to stretch. Strain is a measure of how much an object is being stretched. Strain is the ratio of extension to the original length.
- The formula for strain is: $\epsilon=\frac{\Delta l}{l_0}=\frac{l-l_0}{l_0}=\frac{l}{l_0}-1$
- Where $l_0$ is the original length of some bar being stretched, and $I$ is its length after it has been stretched. $\Delta I$ is the extension of the bar, the difference between these two lengths.
Calculating Young’s Modulus
- Young’s Modulus is a measure of the stiffness of a material. It is defined as the ratio of stress to strain. It states how much a material will stretch (i.e., how much strain it will undergo) as a result of a given amount of stress.
- The formula for calculating it is: $E=\frac{\sigma}{\epsilon}$
- Strain is unit less so Young’s Modulus has the same units as stress, i.e. $\mathrm{N} / \mathrm{m}^2$ or $\mathrm{Pa}$.
Tensile strength \& Yield strength
Tensile Strength
Tensile strength which is also known as Ultimate tensile strength or ultimate strength is the maximum stress that a material can withstand while being stretched or pulled before failing or breaking. Tensile strength is the opposite of compressive strength and the values can be quite different.
Yield Stress or Yield strength or Yield point
The yield stress is the level of stress at which a material will deform permanently. This is also known as Yield strength or Yield point. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed.
It can be experimentally determined from the slope of a stressstrain curve created during tensile tests conducted on a sample of the material.
- The value of the Young’s Modulus is quoted for various materials but the value is only approximate.
- This is because Young’s Modulus can vary considerably depending on the exact composition of the material.
- For example, the value for most metals can vary by $5 \%$ or more, depending on the precise composition of the alloy and any heat treatment applied during manufacture.
- If a big force only produces a small extension then the material is ‘stiff’ and $E$ is a big value. If a force produces a big extension then the material is not very stiff – it is easier to stretch and the value of $\mathrm{E}$ will be smaller.
An experiment to measure the Young’s Modulus
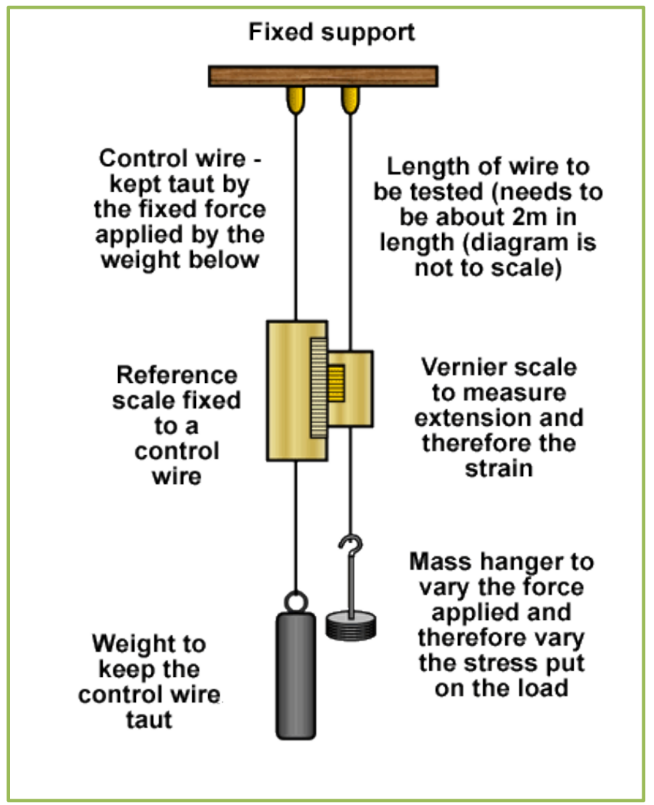
An experiment to measure the Young’s Modulus (continued)
- To minimize errors the control wire is the same length, diameter and material as the test wire. This means that errors due to expansion (from the surroundings) during the experiment are avoided as the test wire and control wire would both expand by the same amount and the scale would adjust position and eliminate the error.
- The wire must have no kinks in it otherwise there will be big extensions due to the wire straightening out rather than just stretching.
- Care must be taken that the limit of proportionality is not exceeded. This can be checked by removing the load after each addition of the weight. If the limit has not been exceeded the wire should return to the length it was before the weight was added.
- The wire is as long as possible (usually about $2 \mathrm{~m}$ long) and it is as thin as possible so that as big an extension as possible can be recorded. (A typical extension for a $5 \mathrm{~N}$ loading will be $1 \mathrm{~mm}$ ).
An experiment to measure the Young’s Modulus (continued)
• The test wire is loaded with the weight hanger so that it is taut before readings are taken.
• The vernier scale is read and the result recorded as addition of 0N.
• Weights – usually starting at 0N and increasing in 5N increments to 100N – are then added and a reading of the vernier scale is taken at each addition.
• The experiment should be repeated twice and any anomalous results repeated and checked.
• A graph of load against extension is plotted. It should be a straight line through the origin (provided measurements are accurate).
• The gradient of that graph will be F/e. Using that value we can find the value of Young’s Modulus for the wire.
$\begin{aligned} E & =\frac{\text { stress }}{\text { strain }} \\ & =\frac{\frac{\mathrm{A}}{\mathrm{A}}}{\frac{\mathrm{e}}{\ell}}=\frac{\mathrm{F} \ell}{\mathrm{Ae}} \\ & =\ell / \mathrm{A} \times \text { Gradient }\end{aligned}$
