Question
A series of experiments were carried out at different temperatures and the rate of reaction, in mol \(dm^{-3} s^{-1}\), was determined for each. The rate constant for the reaction of propanone \((CH_3COCH_3)\) with iodine (I2) was calculated and the processed data is represented in the following graph.
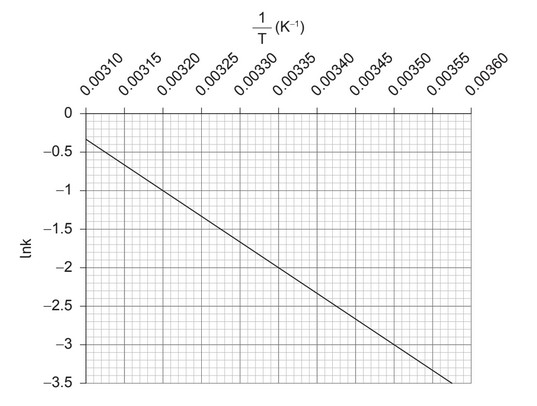
Determine the activation energy for this reaction, stating the units. Use sections 1 and 2 of the data booklet.
Answer/Explanation
Answer:

«two construction lines shown on the graph, and slope calculated:
«(–1.0 – (–3.0))/(0.0032 – 0.0035) =» –6700
«gradient x R = -\(E_a\)»
«6700 x 8.31J \(K^{-1}\) \(mol^{-1}\) /1000=» 56
OR
«6700 x 8.31J \(K^{-1} mol^{-1}\) =» 56000
kJ «\(mol^{-1}\)»
OR
J «\(mol^{-1}\)»
Question
Two chemistry students wished to determine the enthalpy of hydration of anhydrous magnesium sulfate. They measured the initial and the highest temperature reached when anhydrous magnesium sulfate, \({\text{MgS}}{{\text{O}}_{\text{4}}}{\text{(s)}}\), was dissolved in water. They presented their results in the table below.

The students repeated the experiment using 6.16 g of solid hydrated magnesium sulfate, \({\text{MgS}}{{\text{O}}_{\text{4}}} \bullet {\text{7}}{{\text{H}}_{\text{2}}}{\text{O(s)}}\), and \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of water. They found the enthalpy change, \(\Delta {H_2}\) , to be \( + {\text{18 kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\).
The enthalpy of hydration of solid anhydrous magnesium sulfate is difficult to determine experimentally, but can be determined using the diagram below.

(i) Calculate the amount, in mol, of anhydrous magnesium sulfate.
(ii) Calculate the enthalpy change, \(\Delta {H_1}\), for anhydrous magnesium sulfate dissolving in water, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\). State your answer to the correct number of significant figures.[2]
(i) Determine the enthalpy change, \(\Delta H\), in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), for the hydration of solid anhydrous magnesium sulfate, \({\text{MgS}}{{\text{O}}_{\text{4}}}\).
(ii) The literature value for the enthalpy of hydration of anhydrous magnesium sulfate is \( – 103{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\). Calculate the percentage difference between the literature value and the value determined from experimental results, giving your answer to one decimal place. (If you did not obtain an answer for the experimental value in (b)(i) then use the value of \( – 100{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\), but this is not the correct value.)[2]
Another group of students experimentally determined an enthalpy of hydration of \( – 95{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}\). Outline two reasons which may explain the variation between the experimental and literature values.[2]
Magnesium sulfate is one of the products formed when acid rain reacts with dolomitic limestone. This limestone is a mixture of magnesium carbonate and calcium carbonate.
(i) State the equation for the reaction of sulfuric acid with magnesium carbonate.
(ii) Deduce the Lewis (electron dot) structure of the carbonate ion, giving the shape and the oxygen-carbon-oxygen bond angle.
Lewis (electron dot) structure:
Shape:
Bond angle:
(iii) There are three possible Lewis structures that can be drawn for the carbonate ion, which lead to a resonance structure. Explain, with reference to the electrons, why all carbon-oxygen bonds have the same length.
(iv) Deduce the hybridization of the carbon atom in the carbonate ion.[6]
Answer/Explanation
Markscheme
(i) \(n{\text{(MgS}}{{\text{O}}_4}{\text{)}} = \left( {\frac{{3.01}}{{120.37}} = } \right)0.0250{\text{ (mol)}}\);
(ii) energy released \( = 50.0 \times 4.18 \times 9.7 \times 2027{\text{ (J)}}/2.027{\text{ (kJ)}}\);
\(\Delta {H_1} = – 81{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Award [2] for correct answer.
Award [2] if 53.01 is used giving an answer of –86 (kJ mol–1).
Award [1 max] for +81/81/+86/86 (kJ mol−1).
Award [1 max] for –81000/–86000 if units are stated as J mol−1.
Allow answers to 3 significant figures.
(i) \(\Delta H{\text{ (}} = \Delta {H_1} – \Delta {H_2}{\text{)}} = – 99{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ – 1}}{\text{)}}\);
Award [1] if –86 is used giving an answer of –104 (kJ mol–1).
(ii) \(\frac{{(103 – 99)}}{{103}} \times 100 = 3.9\% \);
Accept answer of 2.9% if –100 used but only if a value for (b)(i) is not present.
Award [1] if –104 is used giving an answer of 1.0% .
Accept correct answers which are not to 1 decimal place.
\({\text{MgS}}{{\text{O}}_{\text{4}}}\) not completely anhydrous / OWTTE;
\({\text{MgS}}{{\text{O}}_{\text{4}}}\) is impure;
heat loss to the atmosphere/surroundings;
specific heat capacity of solution is taken as that of pure water;
experiment was done once only so it is not scientific;
density of solution is taken to be \({\text{1 g}}\,{\text{c}}{{\text{m}}^{ – 3}}\);
mass of \({\text{7}}{{\text{H}}_2}{\text{O}}\) ignored in calculation;
uncertainty of thermometer is high so temperature change is unreliable;
literature values determined under standard conditions, but this experiment is not;
all solid not dissolved;
(i) \({{\text{H}}_2}{\text{S}}{{\text{O}}_4}{\text{(aq)}} + {\text{MgC}}{{\text{O}}_3}{\text{(s)}} \to {\text{MgS}}{{\text{O}}_4}{\text{(aq)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}} + {{\text{H}}_2}{\text{O(l)}}\);
Ignore state symbols.
Do not accept H2CO3.
(ii)  ;
;
Accept crosses, lines or dots as electron pairs.
Accept any correct resonance structure.
Award [0] if structure is drawn without brackets and charge.
Award [0] if lone pairs not shown on O atoms.
shape: trigonal/triangular planar;
bond angle: 120° ;
Accept answers trigonal/triangular planar and 120° if M1 incorrect, but no other answers should be given credit.
(iii) (pi/\(\pi \)) electrons are delocalized/spread over more than two nuclei / charge spread (equally) over all three oxygens;
(iv) \({\text{s}}{{\text{p}}^{\text{2}}}\);
Examiners report
The use of 3.01 for the mass in the expression in \(Q = mc\Delta T\) was common, candidates were able to score in the subsequent parts and many did so, although there was often a confusion between the value Q and the required answer for \(\Delta H\). In part c) most candidates understood the error due to heat loss, but few scored the second mark, usually quoting an answer involving an error generally that was far too vague. The inability to construct a balanced equation was disappointing, many lost credit for giving \({{\text{H}}_{\text{2}}}{\text{C}}{{\text{O}}_{\text{3}}}\) as a product. The score for the structure of the carbonate ion was often lost due to the failure to show that a charge is present on the ion, however, the shape and bond angle were known well, as was delocalisation and hybridisation.