Question
Reverse Polish notation (RPN) is a method used to represent mathematical expressions so they can be evaluated without the need for parentheses.
An expression written in this form is known as postfix notation, whereas an expression written the traditional way is known as infix notation.
For example:
Infix notation: $(8-5) * 7$
Postfix notation: $85-7$ *
Both the infix and postfix expressions have the same result: 21
RPN expressions are evaluated from left to right as follows:
- Each character is checked,
- if it is a digit, it is pushed onto a stack.
- if it is a mathematical operator, the last two digits are popped from the stack and evaluated as though the current operator was between them. The result of this operation is then pushed back onto the stack.
- The process is repeated until all the characters in the RPN expression have been used.
- The value left in the stack is the result of the expression.
A collection named RPN already stores an expression formatted in Reverse Polish notation.
The algorithm reads the values from the collection and, using a stack data structure, evaluates it.
RPN.resetNext()
loop while RPN.hasNext()
VALUE = RPN.getNext()
loop while not (VALUE = “+” or VALUE = “-” or VALUE = “*” or VALUE = “/”)
stack.push(VALUE)
VALUE = RPN.getNext()
end loop
OPERAND2 = stack.pop()
OPERAND1 = stack.pop()
if VALUE = “+” then
NEW_VAL = OPERAND1 + OPERAND2
stack.push(NEW_VAL)
end if
if VALUE = “-” then
NEW_VAL = OPERAND1 – OPERAND2
stack.push(NEW_VAL)
end if
if VALUE = “*” then
NEW_VAL = OPERAND1 * OPERAND2
stack.push(NEW_VAL)
end if
if VALUE = “/” then
NEW_VAL = OPERAND1 / OPERAND2
stack.push(NEW_VAL)
end if
end loop
RESULT = stack.pop()
output “The result is: “, RESULT
An alternative data structure in which the expression used in part (a) may be stored is a binary tree. If the tree is traversed using postorder tree traversal, the output is formatted in RPN.
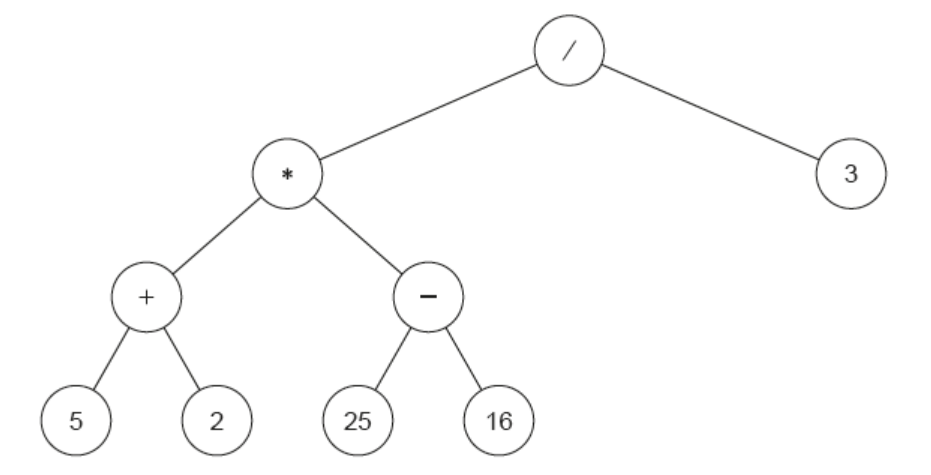
a. Copy and complete the trace table for the algorithm using the RPN collection data:
$
52+2516-* 3 /
$

▶️Answer/Explanation
Ans:
a. )
Award [1] for correct values in VALUE column;
Award [1] for correct values of OPERAND2, OPERAND1 and NEW_VAL when VALUE is ‘+’;
Award [1] for correct values of OPERAND2, OPERAND1 and NEW_VAL when VALUE is ‘-‘;
Award [1] for correct values of OPERAND2, OPERAND1 and NEW_VAL when VALUE is ‘*‘;
Award [1] for correct values of OPERAND2, OPERAND1 and NEW_VAL when VALUE is ‘ $/$ ‘;
Award [1] correct output: ‘The result is: 21’;
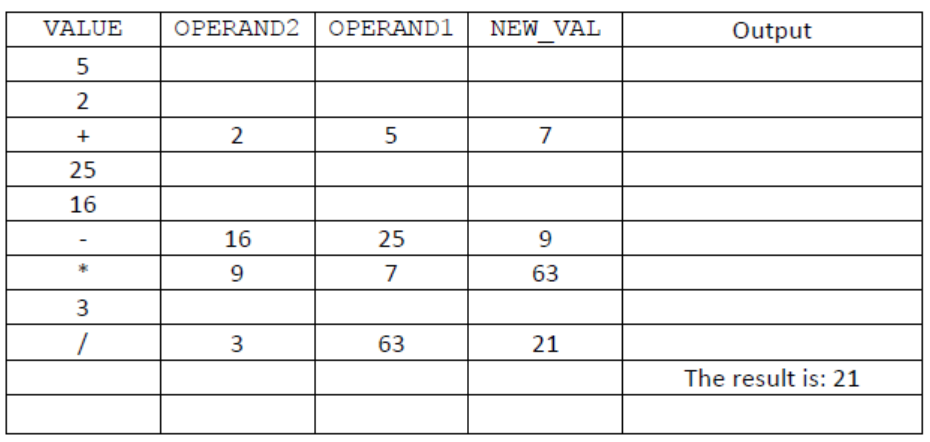
Note: The trace table may be differently presented.
Note: Allow Follow Through.
b. )
A stack is a last in first out (LIFO) / first in last out (FILO) data structure;
… which means data is popped off the stack in the reverse order to which it was pushed;
In the expression, it is important to evaluate some of the values in a certain order(to obtain the correct result);
For example, 25 – 16 would give the wrong value if it was evaluated as $16-25$;
Pushing items onto a stack and then popping them off reverses the order;
To evaluate e.g. “10 2 ” we must treat it as “do the operation on the operands 10 and 2″/ i.e. we have to access the operator before we can apply it to the operands;
A stack achieves the reversing of the order of the operators and their operands as a group (but it also reverses the operands which must be fixed);
c. )
Start from the root node;
If the root is null, return immediately;
Traverse left subtree;
Traverse right subtree;
Visit root;
start from the root node (for example traverse (root)) ;
terminate traversal (and backtrack) when/if root equals null;
(before visiting the root node) traverse (and visit/process/output) each node in the left subtree (i.e., traverse(root.left));
(before visiting the root node) traverse (and visit/process/output) each node in the right subtree (i.e., traverse(root.right));
visit/output/process root (for example, output(root));
d.)
Award [1] if the answer contains no more than one error.
$
(5+2) *(25-16) / 3
$
Note to examiners: Ignore the brackets – these represent the completely correct mathematical expression, but they are not read from the tree. Some candidates might include them because they realise that they may be needed so the expression works correctly.
Question
The flowchart below represents an algorithm that allows a user to enter the number of sides, length of side and apothem (see diagram below) for a regular polygon. It then calculates and outputs the area and perimeter of this shape.
Worked example: a regular hexagon
Number of sides $=6$
Length of side $=10 \mathrm{~cm}$
Apothem $=8.66 \mathrm{~cm}$
Perimeter $=$ Number of sides $\times$ Length of side
$=6 \times 10$
$=60 \mathrm{~cm}$
Area $=\frac{\text { Perimeter } \times \text { Apothem }}{2}$
$=\frac{60 \times 8.66}{2}$
$=259.8 \mathrm{~cm}^2$
From the flowchart, pseudocode is to be created that will include sub-programs to calculate and return the perimeter and area of the shape.
a.i). Construct pseudocode for the body of the following sub-program to calculate and return the perimeter of the shape. [2]
SUB_PERIMETER(NUM_SIDES, LENGTH_SIDE)
// Pseudocode to be added
end SUB_PERIMETER
a.ii.)Construct a similar sub-program to the one in part (i) to calculate and return the area of the shape.[4]
You must use an appropriate name for the sub-program and appropriate names for the parameters.
a.iii)Construct pseudocode based on the flowchart to collect input from the user, call the sub-programs created in parts (i) and (ii), and output the[5]
results.
b. Without using pseudocode, explain how your algorithms could be altered to also find the area and circumference of a circle. [4]
Note:
Area of circle $=\pi r^2$
Circumference of circle $=2 \pi \mathrm{r}$
▶️Answer/Explanation
Ans:
a.i. )
Award [1] for a correct formula that uses the passed arguments;
Award [1] for a return statement;
Example 1:
SUB_PERIMETER (NUM_SIDES, LENGTH_SIDE)
/ Pseudocode to be added
return NUM_SIDES * LENGTH_SIDE
End SUB_PERIMETER
a.ii)
Award [1] for a correct sub-program (function) defined with end statement;
Award [1] for the correct arguments passed;
Award [1] for the correct use of return;
Award [1] for the correct formula used;
Example 1:
SUB_AREA (PERIM, APOTHEM)
$A R E A=$ PERIM * APOTHEM $/ 2$
return AREA
end SUB_AREA
a.iii)
Award [1] for all three correct inputs;
Award [1] for all three inputs with appropriate prompts;
Award [1] for the correct definition of PERIM;
Award [1] for the correct call of perimeter sub-program, including variables/arguments passed;
Award [1] for the correct call of area sub-program, including variables/arguments passed;
Award [1] for the return/output of both values;
Example 1:
//Main Program
output “Number of sides?”
input NUM_SIDES
output “Length of each side?”
input LENGTH_SIDE
output “Length of apothem?”
input APOTHEM
PERIM = SUB_PERIMETER (NUM_SIDES, LENGTH_SIDE)
output “Perimeter is “, PERIM
output “Area is “, SUB_AREA (PERIM, APOTHEM)
b. )
Award [1] for determining whether the shape is a polygon or a circle
Award [1] for inputting the radius (if a circle);
Award [1] for the creation of new subprogram (for area) $O R$
changing values of input parameters for the existing one (SUB_AREA) $O R$
the calculation using correct formula (as given in the question paper $P I$ * $R A D I U S$ * $R A D I U S$ )
Award [1] for the creation of a new subprogram (for circumference) $O R$
appropriately changing values of input parameters to the existing one (SUB_PERIMETER) OR
the calculation using formula (as given in the question paper $2 * P I * R A D I U S$ )
Award [1] for calling both subprograms / outputting both values
Award [1] if after the alteration of the algorithm, it should still be able to calculate the area and the perimeter of the polygon as well as the area the circumference of the circle
Example answer 1 (with existing subprograms, after inputting the three values: NUM_SIDES, LENGTH_SIDE, APOTHEM): check if the inputted value for the NUM_SIDES is 1 or 0 (then the shape is a circle);
then inputted value for LENGTH_SIDE is to be used as radius;
2*3.14 should be set as NUM_SIDES and LENGTH_SIDE as APOTHEM;
call already written sub-programs(SUB_AREA and SUB_PERIMETER) so that algorithm calculates/finds correct area of circle and circumference; if the shape is not a circle then code (as in Part(a)) for the polygon ( no other changes needed);
Example answer 2 (with new subprograms for area and circumference created):
construct two new sub-programs (for example, getCircleArea and getCircumference) ;
(in the main program) ask the user if the shape is a polygon or a circle;
if it is a polygon then code is as written in part a (no changes);
if it is a circle then ask the user to input the radius;
call both new subprograms to output area and circumference/ call the getCircleArea(radius) to find area and getCircumference(radius) sub-program to find circumference;
Example answer 3 (with simple if statement and formulas given in the question paper):
ask user to input if the shape is circle and use if statement to check this input value;
if not circle then code for the polygon (as written in part a);
otherwise (it is circle!) input radius;
calculate area;
and circumference using formulas given in the question;
Note to examiners: there may be other examples of correct answers.
