Question
The array DATA_ARR[] is a one-dimensional array of 12 integers.

Algorithm 1 represents a method of searching the array DATA_ARR [ ] to see if it contains a specific value.
Algorithm 1
input TO_FIND
LIMIT = 11
LOC = FALSE
ITERATE $=0$
loop while not LOC and ITERATE <= LIMIT
$\quad$ if DATA_ARR[ITERATE $]=$ TO_FIND then
$\quad$ LOC = TRUE
$\quad$ end if
ITERATE = ITERATE + 1
end loop
if LOC then
output TO_FIND, “is in the array”
else
output TO_FIND, “is NOT in the array”
end if
Algorithm 2 represents an alternative method of searching the array DATA_ARR[] to see if it contains a specific value.
Algorithm 2
input TO_FIND
LOC = FALSE
LOW_LIM = 0
UP_LIM = 11
loop while LOW_LIM <= UP_LIM and LOC = FALSE
MID_VAL = (LOW_LIM + UP_LIM) div 2
if DATA_ARR[MID_VAL] = TO_FIND then
LOC = TRUE
else
if TO_FIND < DATA_ARR[MID_VAL] then
UP_LIM = MID_VAL – 1
else
LOW_LIM = MID_VAL + 1
end if
end if
end loop
if LOC = TRUE then
output TO_FIND, “is in the array”
else
output TO_FIND, “is NOT in the array”
end if
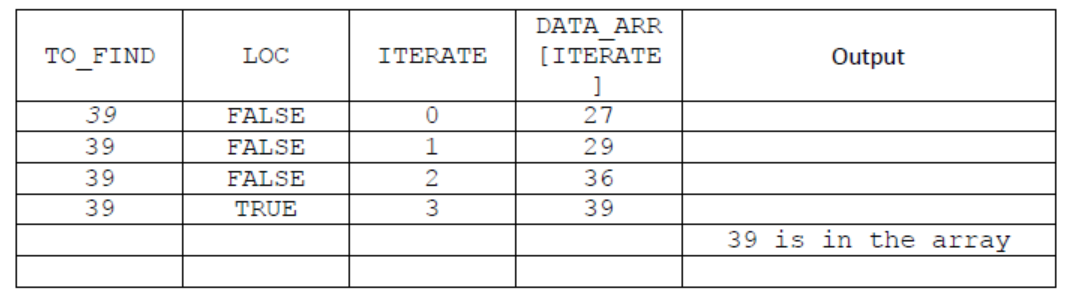
a.)Copy and complete the trace table for Algorithm 1 using TO_FIND = 39.[4]
The first value of the first row has been done for you.

b. State the constant used in Algorithm 1. [1]
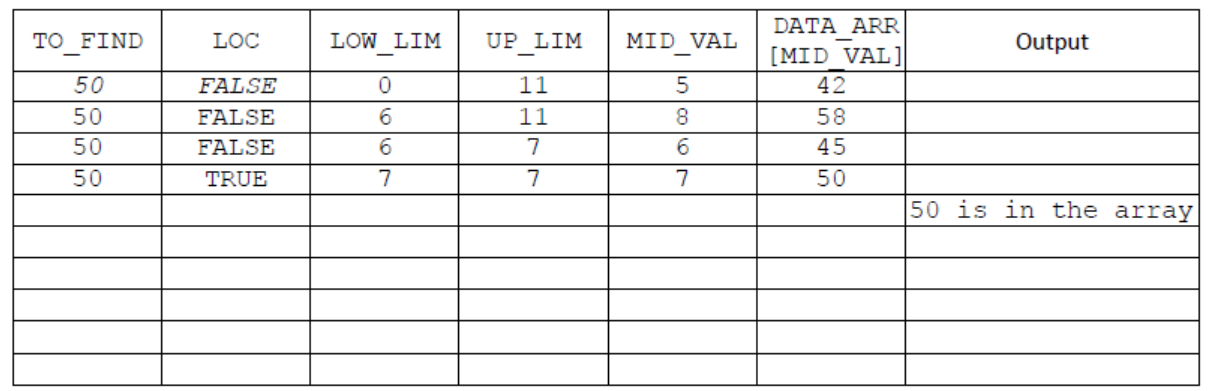
c. Copy and complete the trace table for Algorithm 2 using TO_FIND $=50$.[4]
The first two values of the first row have been done for you.

d. Outline why MID_VAL could not be a constant. [1]
e. Evaluate the use of a sequential search and a binary search including the advantages and disadvantages of each. [5]
▶️Answer/Explanation
Ans:
a. )
Award [1] for TO_FIND and Loc columns;
Award [1] for ITERATE column;
Award [1] for DATA_ARR [ITERATE] column;
Award [1] for the correct output;
b. )
LIMIT
c. )
Award [1] for Low_LIM column;
Award [1] for UP_LIM column;
Award [1] for MID_VAL and DATA_ARR [MID_VAL] columns;
Award [1] for TO_FIND, LOC and Output columns;
d.)
The value (of MID_VAL) changes during the operation of the algorithm;
e.)
The algorithm searches through every element in the array starting at the beginning and working through one after the other; … until the required item is found;
This method is potentially slow if the data set is large and the required element is towards the end of the list; The data does not need to be in any particular order;
Award $[3$ max] for binary search
The data must be sorted before it is stored;
After comparing the data set with the target data, half of the data can be discounted using a simple condition; …enabling the target to be more quickly located;
Note to examiners: Big O notation is not on the syllabus so answers with reference to this are not expected, however, if this type of answer is seen, please allow, for example:
Sequential: main disadvantage is $\mathrm{O}(\mathrm{N})$ so inefficient; advantage is that it works with an unsorted array;
Binary search: main advantage is that it’s efficient as it’s $O(\log n)$;
disadvantage is that the array must be sorted (and so must be sortable – not all data has a defined sort order);
Binary search cannot be performed on a linked list but a sequential search can;
Question
A teacher would like a simple program to store the names, marks and grades of students in a set of three parallel one-dimensional arrays called NAME[], MARK[] and GRADE[] .
The grade boundaries for the individual grades are shown below
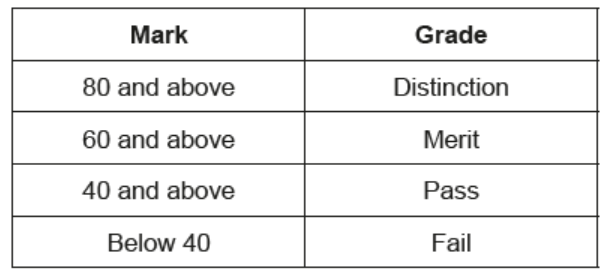
The class has 30 students.
a.Identify two components in a conditional statement.[2]
b.Construct an algorithm using pseudocode to take the marks that have been stored in MARK[], convert them into the appropriate grade and store the calculated grades in GRADE[].[5]
c.Outline how the name, mark and grade in the three arrays correspond to the same student.[2]
d.Construct an algorithm using pseudocode to output the names and grades of all students who achieve a grade of Merit or Distinction.[3]
e.)Explain how you would change your algorithm in part (d) to allow a user to choose a grade and output the names and marks of the students who have achieved this grade.[3]
▶️Answer/Explanation
Ans:
a. )
if;
then;
else ;
b. )
Award [1] for an appropriate loop with correct loop parameters to cover 30 array elements/all students
Award [1] for correct use of indexes in two arrays (MARK and GRADE)
Award [1] for each if statement with correct condition and grade assignment up to [4].
Note to examiners: Award [4] if candidate has correctly used an alternative conditional statement such as switch/ case.
Example answer 1:
loop COUNTER from 0 to 29
if MARK[COUNTER] >= 80
then GRADE[COUNTER] = “Distinction”
else
if MARK[COUNTER]>˝= 60
then GRADE[COUNTER] = “Merit”
else
if MARK[COUNTER} >= 40
then GRADE[COUNTER] = “Pass”
else
GRADE[COUNTER] = “Fail”
end if
end if
end if
end loop
Example answer 2:
COUNTER = 1
loop while COUNTER <= 30
if MARK[COUNTER-1] >= 80
then GRADE[COUNTER-1] = “Distinction”
end if
if MARK[COUNTER-1] >= 60 and MARK[COUNTER-1] < 80
then GRADE[COUNTER-1] = “Merit”
end if
if MARK[COUNTER-1} >= 40 and MARK[COUNTER-1] < 60
then GRADE[COUNTER-1] = “Pass”
end if
if MARK[COUNTER-1} < 40
GRADE[COUNTER-1] = “Fail”
end if
COUNTER = COUNTER + 1
end loop
c. )
Three arrays are parallel/ they have the same number of elements/ the same length; the same array index can be used to represent name, grade and mark of the same student/ the array index makes sure that data from the three arrays lines up;
d.)
Award [1] for correct loop to check all students
Award [1] for correct conditional statement checking correct array
Award [1] for correct output
Example answer 1:
loop COUNTER from 0 to 29
if MARK[COUNTER] >= 60 then
output NAME[COUNTER], GRADE[COUNTER]
end if
end loop
Example answer 2:
loop C from 0 to 29
if GRADE [C]. equals ( “Merit”) OR GRADE [C]. equals (“Distinction”)
then
output NAME $[\mathrm{C}]$, GRADE $[\mathrm{C}]$
end if
end loop
e. )
Award [1] for an input statement before the loop;
Award [1] for changing the conditional statement so that it checks the GRADE [] array for the GRADE input (using the same variable)
Award [1] for outputting the name and marks of the student who has achieved the inputted grade
Note to examiners: Accept a written explanation or an amended algorithm that corresponds to candidate’s answer to part(d).
Example 1:
G=input()
COUNTER = 0
loop while COUNTER < 30
if GRADE[COUNTER] = G
then
output(NAME[COUNTER], MARK[COUNTER])
end if
COUNTER = COUNTER + 1
end loop
Question
Construct a trace table for the following algorithm
A = 3
B = 7
loop while B >= A
A = A + 1
output(B − A)
B = B − 1
end loop
▶️Answer/Explanation
Ans:
Award [1] for a trace table with at least three columns.
Award [1] for each correct column (out of the four columns − A, B, B >= A, output).
