Download IITian Academy App for accessing Online Mock Tests and More..
Question
Show that the set \(S\) of numbers of the form \({2^m} \times {3^n}\) , where \(m,n \in \mathbb{Z}\) , forms a group \(\left\{ {S, \times } \right\}\) under multiplication.
Show that \(\left\{ {S, \times } \right\}\) is isomorphic to the group of complex numbers \(m + n{\rm{i}}\) under addition, where \(m\), \(n \in \mathbb{Z}\) .
Answer/Explanation
Markscheme
Closure: Consider the numbers \({2^{{m_1}}} \times {3^{{m_1}}}\) and \({2^{{m_2}}} \times {3^{{n_2}}}\) where M1
\({m_1},{m_2},{n_1},{n_2}, \in \mathbb{Z}\) . Then,
Product \( = {2^{{m_1} + {m_2}}} \times {3^{{n_1} + {n_2}}}\) which \( \in S\) A1
Identity: \({2^0} \times {3^0} = 1 \in S\) A1
Since \(({2^m} \times {3^n}) \times ({2^{ – m}} \times {3^{ – n}}) = 1\) and \({2^{ – m}} \times {3^{ – n}} \in S\) R1
then \({2^{ – m}} \times {3^{ – n}}\) is the inverse. A1
Associativity: This follows from the associativity of multiplication. R1
[6 marks]
Consider the bijection
\(f({2^m} \times {3^n}) = m + n{\rm{i}}\) (M1)
Then
\(f({2^{{m_1}}} \times {3^{{n_1}}}) \times ({2^{{m_2}}} \times {3^{{n_2}}}) = f({2^{{m_1} + {m_2}}} \times {3^{{n_1} + {n_2}}})\) M1A1
\( = {m_1} + {m_2} + ({n_1} + {n_2}){\rm{i}}\) A1
\( = ({m_1} + {n_1}{\rm{i}}) + ({m_2} + {n_2}{\rm{i}})\) (A1)
\( = f({2^{{m_1}}} \times {3^{{n_1}}}) + f({2^{{m_2}}} \times {3^{{n_2}}})\) A1
[6 marks]
Question
The set \({{\rm{S}}_1} = \left\{ {2,4,6,8} \right\}\) and \({ \times _{10}}\) denotes multiplication modulo \(10\).
(i) Write down the Cayley table for \(\left\{ {{{\rm{S}}_1},{ \times _{10}}} \right\}\) .
(ii) Show that \(\left\{ {{{\rm{S}}_1},{ \times _{10}}} \right\}\) is a group.
(iii) Show that this group is cyclic.
Now consider the group \(\left\{ {{{\rm{S}}_1},{ \times _{20}}} \right\}\) where \({{\rm{S}}_2} = \left\{ {1,9,11,19} \right\}\) and \({{ \times _{20}}}\) denotes multiplication modulo \(20\). Giving a reason, state whether or not \(\left\{ {{{\rm{S}}_1},{ \times _{10}}} \right\}\) and \(\left\{ {{{\rm{S}}_1},{ \times _{20}}} \right\}\) are isomorphic.
Answer/Explanation
Markscheme
(i)
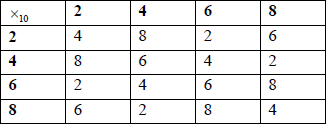A2
Note: Award A1 for one error.
(ii) closure: it is closed because no new elements are formed A1
identity: \(6\) is the identity element A1
inverses: \(4\) is self-inverse and (\(2\), \(8\)) form an inverse pair A1
associativity: multiplication is associative A1
the four group axioms are satisfied
(iii) any valid reason, e.g.
\(2\) (or \(8\)) has order \(4\), or \(2\) (or \(8\)) is a generator A2
[8 marks]
the groups are not isomorphic A1
any valid reason, e.g. \({{\rm{S}}_2}\) is not cyclic or all its elements are self-inverse R2
[3 marks]
Question
The group \(\left\{ {G, + } \right\}\) is defined by the operation of addition on the set \(G = \left\{ {2n|n \in \mathbb{Z}} \right\}\) .
The group \(\left\{ {H, + } \right\}\) is defined by the operation of addition on the set \(H = \left\{ {4n|n \in \mathbb{Z}} \right\}\)
Prove that \(\left\{ {G, + } \right\}\) and \(\left\{ {H, + } \right\}\) are isomorphic.
Answer/Explanation
Markscheme
consider the function \(f:G \to H\) defined by \(f(g) = 2g\) where \(g \in G\) A1
given \({g_1}\), \({g_2} \in G,f({g_1}) = f({g_2}) \Rightarrow 2{g_1} = 2{g_2} \Rightarrow {g_1} = {g_2}\) (injective) M1
given \(h \in H\) then \(h = 4n\) , so \(f(2n) = h\) and \(2n \in G\) (surjective) M1
hence f is a bijection A1
then, for \({g_1}\), \({g_2} \in G\)
\(f({g_1} + {g_2}) = 2({g_1} + {g_2})\) A1
\(f({g_1}) + f({g_2}) = 2{g_1} + 2{g_2}\) A1
it follows that \(f({g_1} + {g_2}) = f({g_1}) + f({g_2})\) R1
which completes the proof that \(\left\{ {G, + } \right\}\) and \(\left\{ {H, + } \right\}\) are isomorphic AG
[7 marks]