Question 16. [Maximum mark: 8]
A particle P moves in a straight line, such that its displacement x at time t (t ≥ 0) is defined by the differential equation x ̇ = x cost(e−sin t ).
At time t = 0 , x = \(\frac{1}{c}\) .
a. By using Euler’s method with a step length of 0.1, find an approximate value
for x when t = 0.3 . [3]
b. By solving the differential equation, find the percentage error in your approximation
for x when t = 0.3 . [5]
▶️Answer/Explanation
(a) \(x_{n}=x_{n-1}+h f(x_{n-1},t_{n-1}\)
\(h = 0.1\),\( f (x,t)= xcost (e^{-sint}\)
\(x_{n}=x_{n-1}+ 0.1x_{n-1} cost_{n-1}e^{-sint}\)
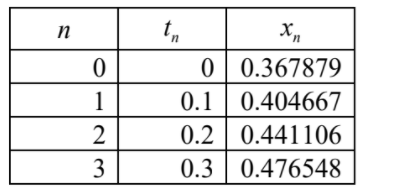
\(x (0.3) ≈ 0.477 (0.476548…)\)
(b) EITHER
\(\int \frac{dx}{x}= \int cost(e^{-sint})dt +c\)
\(ln x = e^{-sint}+ c\)
\(t= 0, x= \frac{1}{e}\Rightarrow c=0\)
\(x = e^{-sint}\)
\(x(0.3)=0.475\)
THEN percentage error \(= |\frac{0.476548.. – 0.475140..}{0.475140..}|\times 100\)
\(= 0.296%(2.96192..)\)
Question
Solve the differential equation \(x\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + 2y = \sqrt {1 + {x^2}} \)
given that \(y = 1\) when \(x = \sqrt 3 \) .
▶️Answer/Explanation
Markscheme
Rewrite the equation in the form
\(\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \frac{2}{x}y = \frac{{\sqrt {1 + {x^2}} }}{x}\) M1A1
Integrating factor \( = {{\rm{e}}^{\int {\left( {\frac{2}{x}} \right)} {\rm{d}}x}}\) M1
\( = {{\rm{e}}^{2\ln x}}\) (A1)
\( = {x^2}\) A1
The equation becomes
\(\frac{{\rm{d}}}{{{\rm{d}}y}}(y{x^2}) = x\sqrt {1 + {x^2}} \) M1
\(y{x^2} = \frac{1}{3}{(1 + {x^2})^{\frac{3}{2}}} + C\) A1
\(3 = \frac{1}{3} \times 8 + C \to C = \frac{1}{3}\) M1A1
\(\left[ {{\text{giving }}y{x^2} = \frac{1}{3}\left( {{{\left( {1 + {x^2}} \right)}^{\frac{3}{2}}} + 1} \right)} \right]\)
[9 marks]
Question
Solve the following differential equation\[(x + 1)(x + 2)\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + y = x + 1\]giving your answer in the form \(y = f(x)\) .
▶️Answer/Explanation
Markscheme
Rewrite the equation in the form
\(\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \frac{y}{{(x + 1)(x + 2)}} = \frac{1}{{x + 2}}\) M1
Integrating factor \( = \exp \left( {\int {\frac{{{\rm{d}}x}}{{(x + 1)(x + 2)}}} } \right)\) A1
\( = \exp \left( {\int {\left( {\frac{1}{{x + 1}} – \frac{1}{{x + 2}}} \right){\rm{d}}x} } \right)\) M1A1
\( = \exp \ln \left( {\frac{{x + 1}}{{x + 2}}} \right)\) A1
\( = \frac{{x + 1}}{{x + 2}}\) A1
Multiplying by the integrating factor,
\(\left( {\frac{{x + 1}}{{x + 2}}} \right)\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \frac{y}{{{{(x + 2)}^2}}} = \frac{{x + 1}}{{{{(x + 2)}^2}}}\) M1
\( = \frac{{x + 2}}{{{{(x + 2)}^2}}} – \frac{1}{{{{(x + 2)}^2}}}\) A1
Integrating,
\(\left( {\frac{{x + 1}}{{x + 2}}} \right)y = \ln (x + 2) + \frac{1}{{x + 2}} + C\) A1A1
\(y = \left( {\frac{{x + 2}}{{x + 1}}} \right)\left\{ {\ln (x + 2) + \frac{1}{{x + 2}} + C} \right\}\) A1
[11 marks]
Question
Given that \(\frac{{{\rm{d}}x}}{{{\rm{d}}y}} + 2y\tan x = \sin x\) , and \(y = 0\) when \(x = \frac{\pi }{3}\) , find the maximum value of y.
▶️Answer/Explanation
Markscheme
integrating factor \( = {{\rm{e}}^{\int {2\tan xdx} }}\) M1
\( = {{\rm{e}}^{2\ln \sec x}}\) A1
\( = {\sec ^2}x\) A1
it follows that
\(y{\sec ^2}x = \int {\sin x{{\sec }^2}x{\rm{d}}x} \) M1
\( = \int {\sec x\tan x{\rm{d}}x} \) (A1)
\( = \sec x + C\) A1
substituting,
\(0 = 2 + C\) so \(C = – 2\) M1A1
the solution is
\(y = \cos x – 2{\cos ^2}x\) A1
EITHER
using a GDC
maximum value of \(y\) is \(0.125\) A2
OR
\(y’ = – \sin x + 4\sin x\cos x = 0\) M1
\( \Rightarrow \cos x = \frac{1}{4}\) (or \(\sin x = 0\) which leads to a minimum)
\( \Rightarrow y = \frac{1}{8}\) A1
[11 marks]
Question
a.(i) Find the range of values of \(n\) for which \(\int_1^\infty {{x^n}{\rm{d}}x} \) exists.
(ii) Write down the value of \(\int_1^\infty {{x^n}{\rm{d}}x} \) in terms of \(n\) , when it does exist.[7]
b.Find the solution to the differential equation
\((\cos x – \sin x)\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + (\cos x + \sin x)y = \cos x + \sin x\) ,
given that \(y = – 1\) when \(x = \frac{\pi }{2}\) .[8]
▶️Answer/Explanation
Markscheme
(i) \(\int_1^b {{x^n}{\rm{d}}x} = \left[ {\frac{{{x^{n + 1}}}}{{n + 1}}} \right]_1^b\) , \(n \ne – 1\) M1
\( = \frac{{{b^{n + 1}}}}{{n + 1}} – \frac{1}{{n + 1}}\) A1
\(\int_1^b {{x^n}{\rm{d}}x} = \left[ {\ln x} \right]_1^b = \ln b\) when \(n = – 1\) A1
if \(n + 1 > 0,\mathop {\lim }\limits_{b \to \infty } \left[ {\frac{{{b^{n + 1}}}}{{n + 1}} – \frac{1}{{n + 1}}} \right]\) does not exist since \({b^{n + 1}}\) increases without limit R1
if \(n + 1 < 0,\mathop {\lim }\limits_{b \to \infty } \left[ {\frac{{{b^{n + 1}}}}{{n + 1}} – \frac{1}{{n + 1}}} \right]\) exists since \({b^{n + 1}} \to 0\) as \(b \to \infty \) R1
if \(n = – 1\) , \(\mathop {\lim }\limits_{b \to \infty } \left[ {\ln b} \right]\) does not exist since \({\ln b}\) increases without limit R1
(so integral exists when \(n < – 1\) )
(ii) \(\int_1^b {{x^n}{\rm{d}}x} = \frac{1}{{n + 1}}\) , \((n < – 1)\) A1
[7 marks]
\((\cos x – \sin x)\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + (\cos x + \sin x)y = \cos x + \sin x\)
\(\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \frac{{\cos x + \sin x}}{{\cos x – \sin x}}y = \frac{{\cos x + \sin x}}{{\cos x – \sin x}}\) M1
IF \({{\rm{e}}^{\int {\frac{{\cos x + \sin x}}{{\cos x – \sin x}}} {\rm{d}}x}} = {{\rm{e}}^{ – \ln (\cos x – \sin x)}} = \frac{1}{{\cos x – \sin x}}\) M1A1A1
\(\frac{y}{{\cos x – \sin x}} = \int {\frac{{\cos x + \sin x}}{{{{(\cos x – \sin x)}^2}}}} {\rm{d}}x\) (M1)
\(\frac{1}{{\cos x – \sin x}} + k\) A1
Note: Award the above A1 even if \(k\) is missing.
\(y = 1 + k(\cos x – \sin x)\)
\(x = \frac{\pi }{2}\) , \(y = – 1\)
\( – 1 = 1 + k( – 1)\) M1
\(k = 2\)
\(y = 1 + 2(\cos x – \sin x)\) A1
Note: It is acceptable to solve the equation using separation of variables.
[8 marks]
