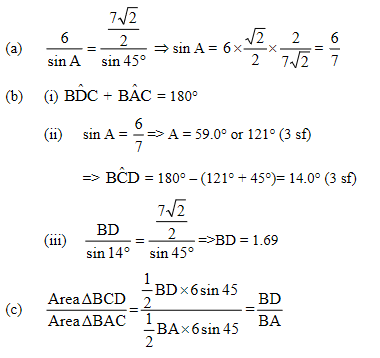Question
The following diagram shows a pentagon ABCDE, with AB = 9.2 cm, BC = 3.2 cm, BD = 7.1 cm, AED = 110o, ADE = 52o and ABD = 60o.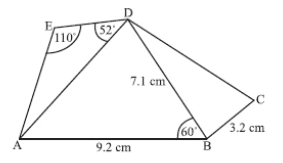
(a) Find AD
(b) Find DE
(c) The area of triangle BCD is 5.68 cm2. Find DBC.
(d) Find AC.
(e) Find the area of quadrilateral ABCD.
Answer/Explanation
Question
The diagram below shows a quadrilateral ABCD. AB = 4, AD = 8, CD = 12, BCD = 25o, BAD = \(\theta\)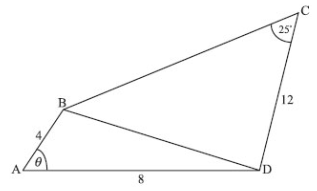
(a) Use the cosine rule to show that \(BD=4\sqrt{5-4cos\theta}\).
Let \(\theta=40^o\).
(b) (i) Find the value of sin CBD.
(ii) Find the two possible values for the size of CBD.
(iii) Given that CBD is an acute angle, find the perimeter of ABCD.
(c) Find the area of triangle ABD.
Answer/Explanation
Question
The diagram below shows a quadrilateral ABCD with obtuse angles ABC and ADC.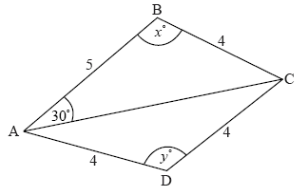
AB = 5 cm, BC = 4 cm, CD = 4 cm, AD = 4 cm, BAC = \(30^o\), ABD = \(x^o\), ADC = \(y^o\).
(a) Use the cosine rule to show that \(AC = \sqrt{41-40 cos z}\).
(b) Use the sine rule in triangle ABC to find another expresssion for AC.
(c) (i) Hence, find x, giving your answer to two decimal places.
(ii) Find AC.
(d) (i) Find y.
(ii) Hence, or otherwise, find the area of triangle ACD.
Answer/Explanation
Ans
(a) \(AC^2=5^2+4^2-2 \times 4 \times 5 cos x \Rightarrow AC=\sqrt{41-40 cos x}\)
(b) \(\frac{AC}{sinx}=\frac{4}{sin30} \Rightarrow AC=8 sin x \)
(c) (i) \(8 sin x = \sqrt{41-40 cos x} \Rightarrow x = 111.32\) to 2 dp
(ii) AC = 8 sin 111.32 = 7.45
(d) (i) \(7.45^2 = 32 – 32 cos y \Rightarrow y = 137\)
(ii) Area \(=\frac{1}{2} \times 4 \times 4 \times sin 137 = 5.42\)
Question
A farmer owns a triangular field ABC. One side of the triangle, [AC], is 104 m, a second side, [AB], is 65 m and the angle between these two sides is 60o.
(a) Use the cosine rule to calculate the length of the third side of the field.
(b) Given that sin\(60^o=\sqrt{3}{2}\), find the area of the field in the form \(p\sqrt{3}\) where \(p\epsilon \mathbb{Z}\)
Let D be a point on [BC] such that [AD] bisects the 60° angle. The farmer divides the field into two parts A1 and A2 by constructing a straight fence [AD] of length x metres, as shown on the diagram below.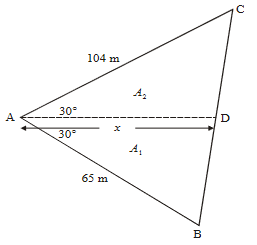
(c) (i) Show that the area of \(A_1\) is given by \(\frac{65x}{4}\)
(ii) Find a similar expression for the area of \(A_2\).
(iii) Hence, find the value of x in the form \(q\sqrt{3}\), where q∈Z.
(d) (i) Explain why sin ADC = sin ADB.
(ii) Use the result of part (i) and the sine rule to show rule to show that \(\frac{BD}{DC}=\frac{5}{8}\).
Answer/Explanation
Ans
(a) \(BC^2=65^2+104^2-2(65)(104) sin 60^o \Rightarrow BC = 91m\)
(b) \(area =\frac{1}{2}(65)(104)sin 60^o = 1690\sqrt{3}\) (p = 1690)
(c) (i) \(A_1=(\frac{1}{2})(65)(x)sin 30^o=\frac{65x}{4}\) (ii) \(A_2=(\frac{1}{2}(104)(x)sin 30^o=26x\)
(iii) \(A_1+A_2 = A \Rightarrow \frac{65x}{4}+26x=1690\sqrt{3} \Rightarrow \frac{169x}{4}=1690\sqrt{3}\)
\(x=\frac{4 \times 1690\sqrt{3}}{169} \Rightarrow x = 40\sqrt{3}\) (q=40)
(d)(i) supplementary angles have equal sines
(ii) using sin rule in ΔADB and ΔACD
\(\frac{BD}{sin30^o}=\frac{65}{sinADB} \Rightarrow \frac{BD}{65}=\frac{sin 30^o}{sin ADB}\)
and \(\frac{DC}{sin30^o}=\frac{104}{sin ADB} \Rightarrow \frac{DC}{104} = \frac{sin30^o}{sin ADC}\)
since sin ADB = sin ADC
\(\frac{BD}{65}=\frac{DC}{104} \Rightarrow \frac{BD}{DC}=\frac{65}{104} \Rightarrow \frac{BD}{DC}=\frac{5}{8}\)
Question
In the diagram below, the points O(0,0) and A(8,6) are fixed. The angle OPA varies as the point P(x,10) moves along the horizontal line y = 10.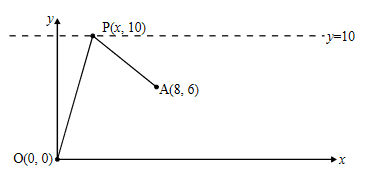
(a) (i) Show that \(AP=\sqrt{x^2-16x+80}\).
(ii) Write down a similar expression for OP in terms of x.
(b) Hence, show that cos OPA=\(\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}}\)
(c) Find, in degrees, the angle OPA when x = 8.
(d) Find the positive value of x such that OPA = 60o.
Let the function f be defined by
\(f(x)=cos OPA=\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}}\), 0≤x≤15\).
(e) Consider the equation f(x)=1
(i) Explain, in terms of the position of the points O, A and P, why this equation has a solution.
(ii) Find the exact solution to the equation.
Answer/Explanation
Ans
(a) (i) \(AP=\sqrt{(x-8)^2+(10-6)^2}=\sqrt{x^2-16x+80}\)
(ii) \(OP=\sqrt{(x-0)^2+(10-0)^2}=\sqrt{x^2+100}\)
(b) \(cos OPA=\frac{AP^2+OP^2-OA^2}{2AP \times OP}=\frac{(x^2-16x+80)+(x^2+100)-(8^2+6^2)}{2\sqrt{x^2-16x+80}\sqrt{x^2+100}}\)
\(=\frac{2x^2-16x+80}{2\sqrt{x^2-16x+80}\sqrt{x^2+100}}=\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}}\)
(c) For \(x = 8, cos OPA=0.780869 \Rightarrow OPA = 38.7^o (3sf)\)
OR \(tanOPA=\frac{8}{10} \Rightarrow OPA=38.7^o (3sf)\)
(d) \(OPA=60^o \Rightarrow cos OPA = 0.5\)
\(0.5=\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}} \Rightarrow x = 5.63\)
(e) (i) f(x) = 1 when cosOPA = 1, hence, when OPA = 0.
This occurs when the points O, A, P are collinear.
(ii) The line (OA) has equation \(y=\frac{3x}{4}\) When y = 10, \(x=\frac{40}{3}(=13\frac{1}{3})\)
OR directly \(x=\frac{40}{3}(=13\frac{1}{3})\)
Question
The diagram shows a triangular region formed by a hedge [AB], a part of a river bank [AC] and a fence [BC]. The hedge is 17 m long and BAC is 29o. The end of the fence, point C, can be positioned anywhere along the river bank.
(a) Given that point C is 15 m from A, find the length of the fence [BC].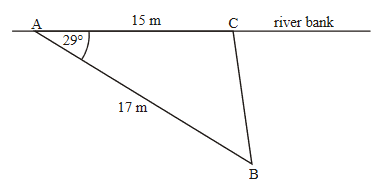
(b) The farmer has another, longer fence. It is possible for him to enclose two different triangular regions with this fence. He places the fence so that ABC is \(85^o\)
(i) Find the distance from A to C.
(ii) Find the area of the region ABC with the fence in this position.
(c) To form the 2nd region, he moves the fencing so that point C is closer to poinnt A. Find the new distance from A to C.
(d) Find the minimum length of fence [BC] needed to enclose a triangular region ABC.
Answer/Explanation
Ans
(a) \(BC^2=15^2+17^2-2(15)(17)cos29^o\)
BC = 8.24 m
(i)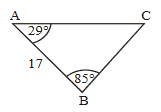
\(ACB=180-(29+85)=66^o\)
\(\frac{AC}{sin85^o}=\frac{17}{sin66^o} \Rightarrow AC=(18.5380…)=18.5m\)
(ii) Area \(=\frac{1}{2}(17)(18.538…)sin29^o=76.4m^2\)
(c) ACB from previous triangle \(=66^o\)
Therefore alternative \(ACB=180-66=114^o (or 29+ 85)\)
\(ABC = 180-(29+114)=37^o\)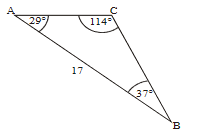
\(\frac{AC}{sin37^o}=\frac{17}{sin114^o} \Rightarrow AC=(11.19986…)=11.2m\)
(d) Min length for BC when \(ACB =90^o\) or diagram showing right triangle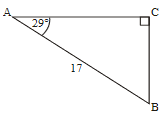
\(sin29^o=\frac{CB}{17} \Rightarrow CB = 17 sin29^o \Rightarrow CB = (8.2417…)=8.24m\)
Question
The points P, Q, R are three markers on level ground, joined by straight paths PQ, QR, PR as shown in the diagram. QR = 9 km, RQP = 35°, QRP = 25°.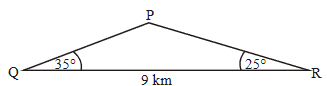
(a) Find the length PR.
(b) Tom sets out to walk from Q to P at a steady speed of 8 km h-1. At the same time, Alan sets out to jog from R to P at a steady speed of a km h-1. They reach P at the same time. Calculate the value of a.
(c) The point S is on [PQ], such that RS = 2QS, as shown in the diagram.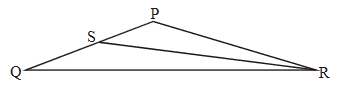
Find the length QS.
Answer/Explanation
Ans
Question
(a) Let \(y=-16x^2+160x-256\). Given that y has a maximum value, find
(i) the value of x giving the maximum value of y;
(ii) this maximum value of y.
The triangle XYZ has XZ = 6, YZ = x, XY = z as shown below. The perimeter of triangle XYZ is 16.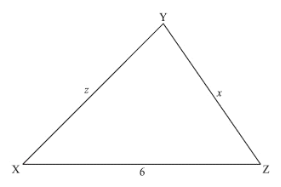
(b) (i) Express z in terms of x.
(ii) Using the cosine rule, express \(x^2\) in terms of x and cos Z.
(iii) Hence, show that \(cosZ=\frac{5x-16}{3x}\)
Let the area of triangle XYZ be A.
(c) Show that \(A^2=9x^2sin^2Z\).
(d) Hence, show that \(A^2=-16x^2+160x-256\).
(e) (i) Hence, write down the maxmum area for triangle XYZ.
(ii) What type of triangle is the with maximum area?
Answer/Explanation
Ans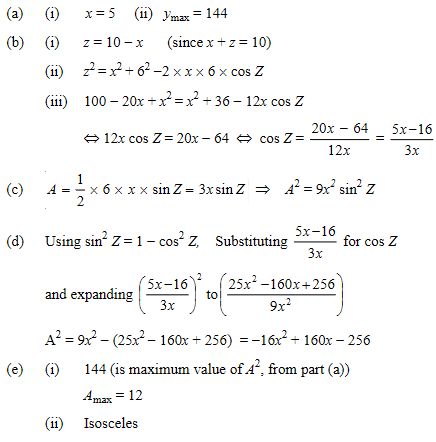
Question
An office tower is in the shape of a cuboid with a square base. The roof of the tower is in the shape of a square based right pyramid.
The diagram shows the tower and its roof with dimensions indicated. The diagram is not drawn to scale.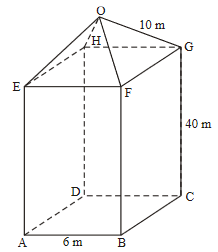
(a) Calculate, correct to three significant figures,
(i) the size of the angle between OF and FG;
(ii) the shortest distance from O to FG;
(iii) the total surface area of the four triangular sections of the roof;
(iv) the size of the angle between the slant height of the roof and the plane EFGH;
(v) the height of the tower from the base to O.
A parrot’s nest is perched at a point, P, on the edge, BF, of the tower. A person at the point A, outside the building, measures the angle of elevation to point P to be 79°.
(b) Find, correct to three significant figures, the height of the nest from the base of the tower.
Answer/Explanation
Ans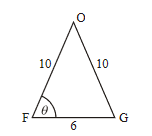
(a) (i) \(cos\theta=(\frac{10^2+6^2-10^2}{(2)(10)(6)} \Rightarrow \theta = 72.5^o (3sf)\)
(ii) h = shortest distance from O to FG \(= 3 tan \theta = 9.53939…=9.54m(3sf)\)
(iii) Area of ΔOFG \(=\frac{1}{2} (10)(6)(sin \theta)\)
toatal surface area of roof \(=4 \times \frac{1}{2}(10)(6)(sin \theta)=114.4727…=114m^2(3s.f.)\)
(iv) Let Φ = angle between slant height (line) and plane EFGH
\(cos \phi =(\frac{3}{h}) \Rightarrow \phi = 71.7^o (3 s.f)\)
(v) H = Height of tower from base to \(O =40+ \sqrt{h^2-3^2}=49.1m(3s.f)\)
(b) Height (BP) \(=\frac{6sin79^o}{sin(90^o-79^o)}=30.9 m(3 s.f.)\)
The diagram shows a triangle ABC in which AC\(=7\frac{\sqrt{2}}{2},BC=6,ABC=45^o\).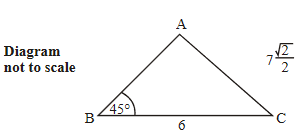
(a) Use the fact that \(sin45^o=\frac{\sqrt{2}}{2}\) to show that sin BAC\(=\frac{6}{7}\).
The point D is on (AB), between A and B, such that \(sin BDC =\frac{6}{7}\).
(b) (i) Write down the value of BDC + BAC.
(ii) Calculate the angle BCD.
(iii) Find the length of [BD].
(c) Show that \(\frac{Area ofΔBDC}{Area of ΔBAC}=\frac{BD}{BA}\).
Answer/Explanation
Ans