Question
The function \(f(x)\) is such that \(f'(x) < 0\) for \(1 < x < 4\). At the point \({\text{P}}(4{\text{, }}2)\) on the graph of \(f(x)\) the gradient is zero.
Write down the equation of the tangent to the graph of \(f(x)\) at \({\text{P}}\).[2]
State whether \(f(4)\) is greater than, equal to or less than \(f(2)\).[2]
Given that \(f(x)\) is increasing for \(4 \leqslant x < 7\), what can you say about the point \({\text{P}}\)?[2]
Answer/Explanation
Markscheme
\(y = 2\). (A1)(A1) (C2)
Note: Award (A1) for \(y = \ldots \), (A1) for \(2\).
Accept \(f(x) = 2\) and \(y = 0x + 2\)
Less (than). (A2) (C2)[2 marks]
Local minimum (accept minimum, smallest or equivalent) (A2) (C2)
Note: Award (A1) for stationary or turning point mentioned.
No mark is awarded for \({\text{gradient}} = 0\) as this is given in the question.
Question
The table given below describes the behaviour of f ′(x), the derivative function of f (x), in the domain −4 < x < 2.
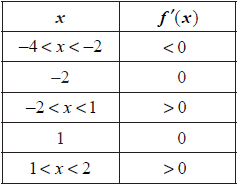
State whether f (0) is greater than, less than or equal to f (−2). Give a reason for your answer.[2]
The point P(−2, 3) lies on the graph of f (x).
Write down the equation of the tangent to the graph of f (x) at the point P.[2]
The point P(−2, 3) lies on the graph of f (x).
From the information given about f ′(x), state whether the point (−2, 3) is a maximum, a minimum or neither. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
greater than (A1)
Gradient between x = −2 and x = 0 is positive. (R1)
OR
The function is increased between these points or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
y = 3 (A1)(A1) (C2)
Note: Award (A1) for y = a constant, (A1) for 3.[2 marks]
minimum (A1)
Gradient is negative to the left and positive to the right or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
Question
Consider the graph of the function \(f(x) = {x^3} + 2{x^2} – 5\).
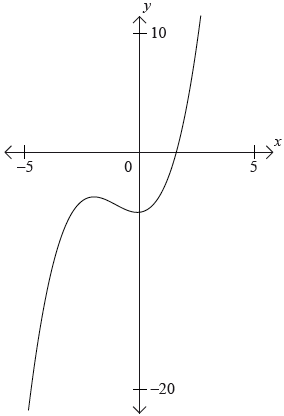
Label the local maximum as \({\text{A}}\) on the graph.[1]
Label the local minimum as B on the graph.[1]
Write down the interval where \(f'(x) < 0\).[1]
Draw the tangent to the curve at \(x = 1\) on the graph.[1]
Write down the equation of the tangent at \(x = 1\).[2]
Answer/Explanation
Markscheme
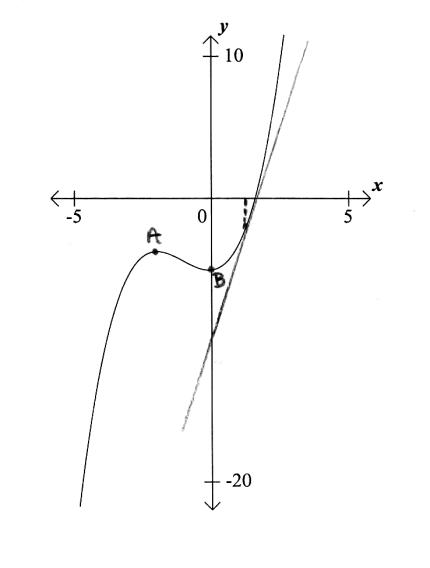
correct label on graph (A1) (C1)[1 mark]
correct label on graph (A1) (C1)[1 mark]
\( – 1.33 < x < 0\) \(\left( { – \frac{4}{3} < x < 0} \right)\) (A1) (C1)[1 mark]
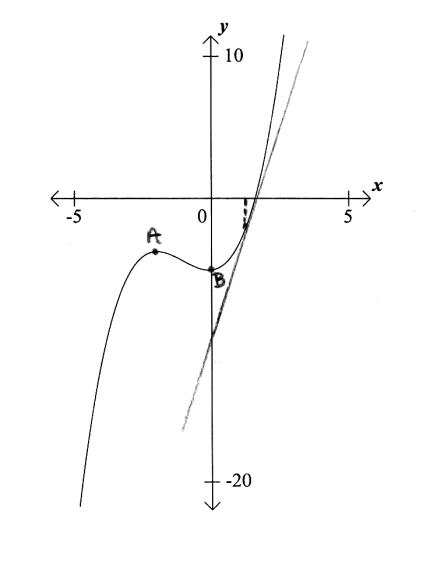
tangent drawn at \(x = 1\) on graph (A1) (C1)[1 mark]
\(y = 7x – 9\) (A1)(A1) (C2)
Notes: Award (A1) for \(7\), (A1) for \(-9\).
If answer not given as an equation award at most (A1)(A0).[2 marks]
Question
Consider the graph of the function \(y = f(x)\) defined below.
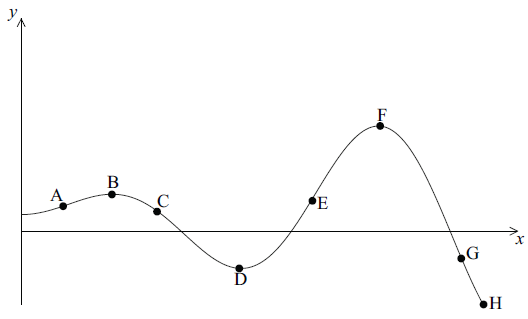
Write down all the labelled points on the curve
that are local maximum points;[1]
where the function attains its least value;[1]
where the function attains its greatest value;[1]
where the gradient of the tangent to the curve is positive;[1]
where \(f(x) > 0\) and \(f'(x) < 0\) .[2]
Answer/Explanation
Markscheme
B, F (C1)
H (C1)
F (C1)
A, E (C1)
C (C2)